По различным схемам

Анализ зависимостей 1.3—1.8 показывает, что:

если в планетарных механизмах, выполненных по схемам а и б (рис.1.2), передаточное отношение в обращенном движении

U₁₄^(H) = (Z ₂*Z₄ / Z₁* Z₃)>2, то:

а) механизм будет работать в режиме редуктора при входном зубчатом колесе 1 и выходном водиле Н, обеспечивая отрицательное передаточное отношение U_1H⁽⁴⁾ >[1], при этом U₁₄^(H) > U_1H⁽⁴⁾ и схема оказывается кинематически невыгодной, так как конструктивно планетарный механизм более сложен, чем механизм с неподвижными осями;

б) при входном водиле Н и выходном зубчатом колесе 1 механизм будет работать в режиме мультипликатора, обеспечив отрицательное передаточное отношение -1< U_H1 ⁽⁴⁾ < 0;

если в планетарных механизмах, выполненных по схемам а и б (рис.1.2), передаточное отношение в обращенном движении 1< U₁₄^(H)< 2, то:

a) при входном зубчатом колесе 1 и выходном водиле Н механизм будет работать в режиме мультипликатора, обеспечив отрицательное передаточное отношение -1< U_1H ⁽⁴⁾ <0;

б) при входном водиле Н и выходном зубчатом колесе 1 механизм будет работать в режиме редуктора, обеспечивая отрицательное передаточное отношение в пределах - ∞ < U_H1 ⁽⁴⁾ < -1;

– если в схемах а и б (рис.1.2) передаточное отношение

0 < U₁₄^(H) < 1, то:

a) при входном зубчатом колесе 1 и выходном водиле Н механизм будет работать в режиме мультипликатора, обеспечив положительное передаточное отношение 0 < U_1H ⁽⁴⁾ < 1;

б) при входном водиле Н и выходном зубчатом колесе 1 механизм будет работать в режиме редуктора, обеспечивая положительное передаточное отношение в пределах 1< U_H1⁽⁴⁾ < + ∞;

– если в планетарных механизмах, выполненных по схемам а и б (рис.1.2), передаточное отношение в обращенном движении U₁₄^(H) =2, то независимо от входного и выходного звеньев, передаточное отношение в планетарном режиме будет равно –1, т.е. входное и выходное звенья будут вращаться с одинаковыми угловыми скоростями, но в разном направлении;

– если в планетарных механизмах, выполненных по схемам а и б (рис.1.2), передаточное отношение в обращенном движении U₁₄^(H) =1 (это возможно при условии, что Z₁ = Z₄ и Z₂ = Z ₃), то при входном зубчатом колесе 1 и выходном водиле Н передаточное отношение U_1Н⁽⁴⁾ =0, т.е. при вращении колеса 1 водило Н будет неподвижно; а при входном водиле Н и выходном зубчатом колесе 1 передаточное отношение U_H1⁽⁴⁾ =1/ (1-1) = ∞, что соответствует режиму заклинивания механизма.

Анализ зависимостей 1.9 – 1.10 показывает, что механизмы, выполненные по схемам в и г, могут обеспечить только положительное передаточное отношение при любом варианте сборки. Если в этих механизмах за входное принять зубчатое колесо, а за выходное – водило, то механизм будет работать в режиме редуктора; при входном водиле и выходном колесе – в режиме мультипликатора. При любом варианте сборки схемы в и г кинематически выгодны.

Если в схемах в и г за входное принять зубчатое колесо 1 с наружным зубом, а за выходное принять водило, то оптимальное передаточное отношение редуктора будет находиться в пределах 1,3< U_1H⁽⁴⁾ <6. Если же в этих схемах принять за входное зубчатое колесо 4 с внутренним зубом, а за выходное водило Н, то передаточное отношение редуктора будет находиться в пределах 1< U_4H⁽¹⁾ <2.

При выполнении курсового проекта студенту рекомендуется самостоятельно назначить входное и выходное звенья для заданной схемы планетарного механизма так, чтобы обеспечить его работу в режиме редуктора.

Следовательно, если двухступенчатый передаточный механизм состоит из пары зубчатых колёс внешнего зацепления (рядная ступень) и планетарной ступени, то вал двигателя и вал рабочей машины будут вращаться в одну сторону у механизмов с планетарной ступенью, выполненной по схемам а и б (передаточное отношение всего механизма положительное); вал двигателя и вал рабочей машины будут вращаться в разные стороны у механизмов с планетарной ступенью, выполненной по схемам в и г (передаточное отношение всего механизма отрицательное).

Последовательность определения передаточного отношения всего механизма и распределение его по ступеням рассмотрим на примере рис.1.3.

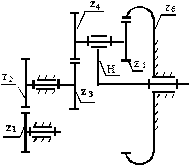
Рис. 1.3. Схема планетарного редуктора.

По заданной угловой скорости выходного вала двигателя и угловой скорости ведущего (входного) вала рабочей машины определяем общее передаточное отношение зубчатой передачи, состоящей из планетарного механизма и одной пары колёс рядного зубчатого зацепления. Так как передаточный механизм включает рядную ступень, состоящую из колёс 1 и 2, и планетарную ступень, выполненную по схеме в (см. рис.1.2), то вал колеса 1 (вал двигателя) и вал водила Н (вал рабочей машины) будут вращаться в разные стороны. Общее передаточное отношение всего механизма будет отрицательным:

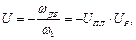(1.11)

где w_дв – угловая скорость входного вала механизма передач (вала

механизма передач, связанного с двигателем);

w₁ – угловая скорость выходного вала механизма передач (вала

механизма передач, связанного с рабочей машиной);

U_пл – передаточное отношение планетарной ступени механизма

передач;

U_p – передаточное отношение рядной ступени механизма передач.

Передаточное отношение рядной ступени редуктора определяется через заданное число зубьев z₁ и z₂ по формуле

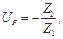(1.12)

где знак минус относится к внешнему зацеплению пары зубчатых колёс 1 и 2.

Из формулы (1.11) с учётом выражения (1.12) определяем передаточное отношение планетарной ступени механизма передач:

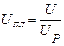. (1.13)

Определив таким образом передаточное отношение U_ПЛ, необходимо назначить входное и выходное звенья планетарной ступени из условия работы механизма в режиме редуктора. В соответствии с выбранными входным и выходным звеньями, составить расчётную схему механизма передач и приступить к подбору числа зубьев колёс.

1.4. Подбор чисел зубьев планетарного зубчатого механизма

При подборе чисел зубьев колёс для выбранной схемы механизма необходимо учесть ряд условий, а именно, выдержать заданное передаточное число, обеспечить соосность зубчатых колёс, выдержать «условие соседства» сателлитов; обеспечить «условие сборки», отсутствие заклинивания; добиться более высокого к.п.д. передачи. При этом необходимо добиваться компактности и простоты конструкции, простоты сборки, равномерности распределения нагрузки между зубьями колёс.

Наиболее простым методом подбора числа зубьев является метод неопределённых сомножителей, при котором подбор ведётся только по двум условиям — передаточному отношению и условию соосности, а проверка — по условию сборки, соседства, заклинивания и наименьшему суммарному числу зубьев. Обеспечение заданного отношения (с допустимой точностью 1…5%) диктуется требованиями точности выполнения технологического процесса. Передаточное отношение планетарной ступени редуктора определяется по зависимости (1.13) с учётом формул (1.1 и 1.12).

Условие соосности требует размещения осей вращения всех колёс на одной прямой. Для схем механизмов, изображенных на рис. 1.2, условие соосности имеет вид:

для схемы а 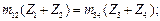(1.14)

для схемы б 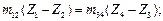(1.15)

для схемы в 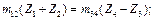(1.16)

для схемы г 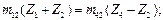(1.17)

где m₁₂, m₃₄ — модуль зацепления колёс 1 и 2, 3, и 4.

В задании на курсовой проект принято m₁₂ = m₃₄ = m.

Выполнение условия соосности необходимо для обеспечения зацепления сателлитов с центральными колёсами и проворачиваемости водила.

Выполнение условия соседства обеспечит размещение сателлитов вокруг центрального колеса (внутри центрального колеса) так, что соседние сателлиты не будут задевать своими зубьями друг друга.

В общем случае для нулевых цилиндрических передач условие соседства имеет следующий вид:

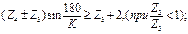(1.18)

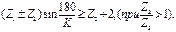(1.19)

В зависимостях (1.18—1.19) берётся знак плюс при внешнем и минус — при внутреннем зацеплении колёс 1—2.

Возможность установки нескольких сателлитов и их одновременного зацепления с центральными колёсами обеспечивается условиями сборки. Условие сборки планетарных механизмов связывает в одно целое число зубьев зубчатых колёс, числа сателлитов и их взаимное расположение.

Для однорядной планетарной передачи (рис. 1.2, г) условие сборки имеет вид

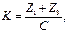(1.20)

где К – число сателлитов, устанавливаемых в планетарный редуктор;

С – целое число зубьев, на которое нужно повернуть подвижное

колесо для установки следующего сателлита.

Для передачи с двойными сателлитами (рис. 1.2, а, в) условие сборки имеет вид

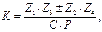(1.21)

где Р — общий наибольший делитель чисел зубьев z₂ и z₃ венцов

сателлита. Знак плюс берётся для схемы в, а минус – для

схем а и б.

Чтобы избежать заклинивания передач внутреннего зацепления, составленных из эвольвентных нулевых колёс, необходимо выбрать число зубьев каждого колеса передачи больше допустимого минимума z_min. Для колёс с внутренними зубьями при угле зацепления a =20° и коэффициенте высоты зуба c =1,0 принимается 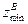=60°; для сцепляющихся с ними колёс с внешними зубьями z^H_min соответственно равно 20 зубьям, а для всей передачи разность чисел зубьев сцепляющихся колёс z_В—z_Н должна быть не менее 8. Во избежание подреза зубьев для передач внешнего зацепления при a =20° и c =1,0 необходимо принять z_min 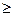17.

Размеры планетарного редуктора определяются суммарными числами зубьев всех колёс. Подбор числа зубьев колёс планетарного редуктора методом неопределённых сомножителей рекомендуется выполнять в предлагаемой ниже последовательности.

1. По приведённой схеме (рис. 1.3) планетарного механизма выразить передаточное отношение через числа зубьев по зависимостям (1.3—1.8).

Если входным является зубчатое колесо 3, а выходным — вал водила Н, то передаточное отношение определяется по формуле

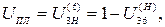(1.22)

где U^(H)₃₆ — передаточное отношение от колеса 3 к колесу 6 редуктора при остановленном водиле Н;

U⁽⁶⁾_3Н — передаточное отношение от колеса 3 к водилу Н при не-

подвижном шестом колесе.

Если по кинематической схеме механизма водило является входным (ведущим) звеном при неподвижном колесе 6, то передаточное отношение определяется по формуле

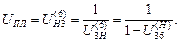(1.23)

Если передаточное отношение планетарной ступени U_пл больше допустимых пределов, то в кинематическую схему передаточного механизма следует включить две планетарные ступени. Передаточное отношение одной планетарной ступени

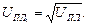(1.24)

Передаточное отношение от колеса 3 к колесу 6 редуктора при неподвижном водиле Н определяется через число зубьев по формуле

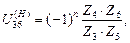(1.25)

где n — показатель, равный числу пар зубчатых колёс планетарного

механизма с внешним зацеплением. В нашем случае n = 1.

Выразив из формул (1.22) и (1.23) передаточное отношение U^(Н)₃₆ обращенного редуктора с учётом зависимости (1.25), получим

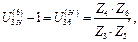(1.26)

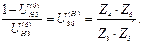(1.27)

2. Из зависимостей (1.26—1.27) определяется численное значение передаточного отношения U^(Н)₃₆. Это число представляется в виде неопределённых сомножителей a, b, c и d следующим образом:

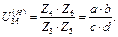(1.28)

Численные значения сомножителей следует определить так, чтобы обеспечивалось заданное передаточное отношение U^(Н)₃₆. При этом необходимо помнить, что неподвижное колесо на схеме должно иметь наибольшее число зубьев и ему должен соответствовать больший из неопределённых сомножителей. В случае иррациональности значений U^(H)₃₆ неопре-делённые сомножители следует подобрать так, чтобы расчётное передаточное отношение отличалось от заданного не более чем на 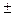5%. Таких численных сомножителей будет бесконечное множество. Необходимо просчитать несколько вариантов и выбрать тот, который удовлетворяет всем условиям: соседства, сборки, заклинивания и имеет наименьшее суммарное число зубьев. Например, пусть задано передаточное отношение

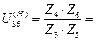6,51.

Округлим данное передаточное отношение на 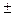5%, что составит 0,32. Тогда расчётное передаточное отношение будет находиться в пределах 6,19≤ U₃₆^{(H )}≤6,83. К расчёту принимаем U₃₆^(Н)= 6,5. В данном случае численное значение передаточного отношения

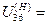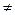6,5 6,51.

Ошибка не превышает + 5%, что допустимо по условию обеспечения передаточного отношения.

Это передаточное отношение можно представить в виде произведения неопределённых сомножителей:

= .

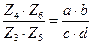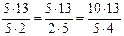В данном случае сомножитель а пропорционален z₄:

b Þ z₆; c Þ z₃; d Þ z₅.

Сомножителями a, b, c, d могут быть любые положительные числа, удовлетворяющие передаточному отношению. Для различных вариантов численные значения этих сомножителей удобно представить в виде табл. 1.1.

Т а б л и ц а 1.1. Численные значения неопределённых сомножителей

Сомножитель	В а р и а н т
1-й	2-й	3-й
a b c d

3. Чтобы обеспечить условие соосности

z₃+z₄=z₆ – z₅, (1.29)

когда все колёса одного модуля, необходимо ввести множители a₁ и a₂. В этом случае условие соосности, выраженное через неопределённые сомножители, примет вид

γ(a + c)a₁= γ(b – d)a₂. (1.30)

Проще всего принять в качестве дополнительных сомножителей a₁= (b –d) и a₂ = (a + c). Тогда условие соосности примет вид

a(b – d)γ + c(b – d) γ = b(a + c) γ – d (a + c) γ. (1.31)

Следовательно,

z₄ = a(b – d)g; z₆ = b(a + c)g;

z₃ = c(b – d) g; z₅ =d(a + c) g, (1.30)

где g – любое положительное число, определяемое из условия

отсутствия подрезания ножек зубьев.

Определение чисел зубьев колёс всех выбранных вариантов приведено в табл. 1.2.

Для всех вариантов коэффициент g определяем из условия отсутствия подрезания ножек зубьев. Определение коэффициента g рассмотрим на примере первого варианта.

Т а б л и ц а 1.2. Определение числа зубьев колёс планетарного редуктора

Расчётные формулы	В а р и а н т ы
1-й	2-й	3-й
z×g1	g1=1	z×g2	g2=1	z×g3	g3=0,4
z4= a(b – d) g z6= b(a + c) g z3= c(b + d) g z5= d(a + c) g z сум	-		-		-

Согласно кинематической схеме (рис. 1.3), колесо z₆ имеет внутренние зубья. Для этого колеса z_min 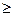60 при a =20° и c =1,0. Следовательно, z₆ =130 g₁ ¢ 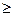60, откуда γ₁ ′ ≥ 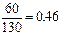. С колесом z₆ находится в зацеплении колесо z₅. Для этого колеса z_min 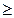20. Следовательно, z₅ =20 g₁ ¢ 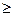20, откуда g₁ ¢¢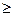 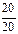=1. Колеса z₃ и z₄ имеют внешнее зацепление. Для этой пары зубчатых колёс z_min >17. В этом случае z₃ = z₄ = 55 g₁ ¢¢¢ 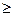17, откуда

g₁ ¢¢¢ 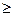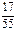=0,3.

Для исключения отсутствия подрезания ножек зубьев в первом варианте следует принять g₁=g₁¢¢= 1. В общем случае коэффициент g принимают из условия отсутствия подрезания ножек зубьев таким, чтобы числа зубьев колёс были целыми. Число зубьев колёс с внутренними зацеплениями в целях уменьшения габаритов редуктора не рекомендуется принимать больше 100. 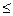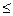Следовательно, числа зубьев колёс должны находиться в диапазоне 17 z 100.

Аналогично определяются коэффициенты g для всех остальных вариантов расчета. В нашем случае g₁= 1, g₂= 1, g₃= 0,4. По принятым значениям g определяем числа зубьев всех колёс во всех вариантах (табл.1.2).

Анализ данных таблицы показывает, что число зубьев, рассчитанное по варианту 1, не удовлетворяет ограничениям по габаритам редуктора, т.е. z₆ =130>100. Поэтому в дальнейшем расчёт по этому варианту производить не следует.

Проверяем расчётные числа зубьев варианта 2 и 3 по условиям соседства

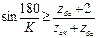или 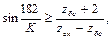(1.31)

и сборки

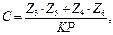(1.32)

где К – число блоков сателлитов (К = 3 – 4);

z_бс – большее из числа зубьев колёс блока сателлитов;

z_ск – число зубьев центрального колеса, с которым в зацеплении

находится сателлит z_бс;

Р – наибольший делитель чисел z₄ и z₅;

С – любое целое число.

Расчёты по условиям (1.31) и (1.32) представлены в табл. 1.3.

Т а б л и ц а 1.3. Определение числа зубьев планетарного редуктора