Колебательный контур. Формула Томсона

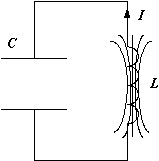
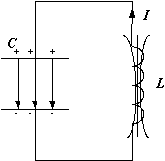
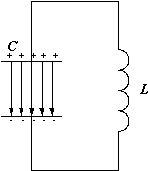
Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым. Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).

Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд + Q ₀, а на другой – заряд - Q ₀. При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией

, (1)

где 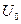– амплитудное (максимальное) напряжение или разность потенциалов на обкладках конденсатора.

После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения 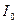. Так как в цепи протекает переменный по величине ток, то в катушке индуцируется ЭДС самоиндукции, которая препятствует разрядке конденсатора. Поэтому процесс разрядки конденсатора происходит не мгновенно, а постепенно. В каждый момент времени разность потенциалов на обкладках конденсатора

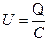(2)

(где 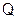– заряд конденсатора в данный момент времени) равна разности потенциалов на катушке, т.е. равна ЭДС самоиндукции

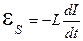. (3)

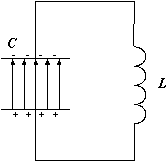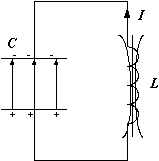Рис.1	Рис.2

Когда конденсатор полностью разрядится 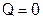и 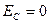, сила тока в катушке достигнет максимального значения 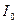(рис.3). Индукция магнитного поля катушки в этот момент также максимальна, а энергия магнитного поля будет равна

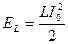. (4)

Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q ₀, но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.

Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.

Рис.3	Рис.4

Перезарядка конденсатора до максимального напряжения 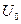произойдет только в том случае, когда в колебательном контуре нет потерь энергии. Такой контур называется идеальным.

В реальных контурах имеют место следующие потери энергии:

1) тепловые потери, т.к. R ¹ 0;

2) потери в диэлектрике конденсатора;

3) гистерезисные потери в сердечнике катушке;

4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что 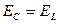, т.е.

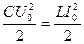. (5)

Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.

В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:

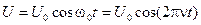, (6)

где n - собственная частота колебательного контура, w₀ = 2pn - собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как

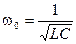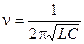или . (7)

Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона

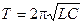. (8)

Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на 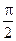. Поэтому зависимость силы тока в цепи от времени будет иметь вид

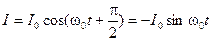. (9)

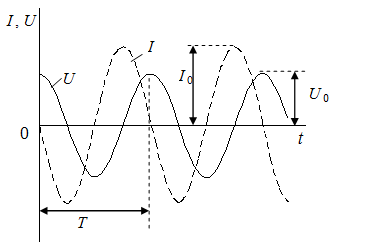
На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.

В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.

Рис.5	Рис.6

Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.