

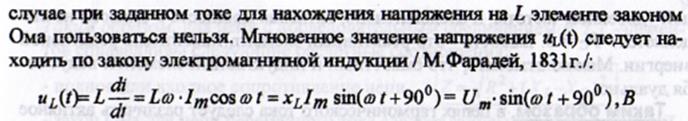

Если к идеальной катушке индуктивности подключить синусоидальное напряжение, то по ней потечет ток.
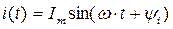 .
.
Этот ток наводит в катушке ЭДС самоиндукции, которая направлена против переменного напряжения и уравновешивает его, т.е.
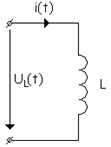
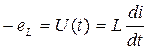 .
.
Следовательно
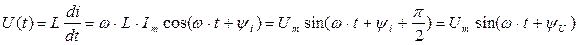 , где
, где 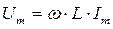 ,
, 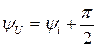 , а сдвиг фаз между напряжением и током
, а сдвиг фаз между напряжением и током 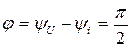 .
.
Из приведенных выражений следует, что в цепи с индуктивностью ток в катушке отстает по фазе от приложенного напряжения на 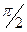 . Графически это можно представить векторной диаграммой и зависимостью тока и напряжения от времени (рис. 59).
. Графически это можно представить векторной диаграммой и зависимостью тока и напряжения от времени (рис. 59).
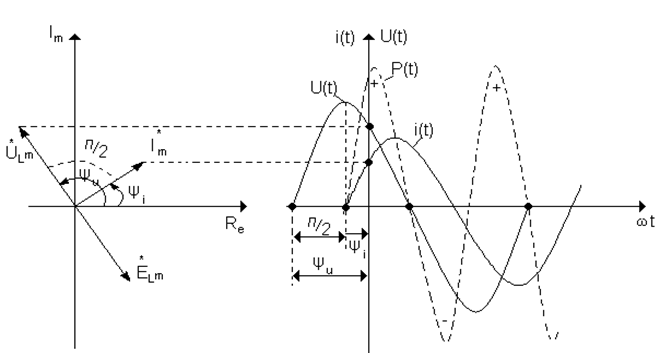
Рис. 59.
Ток в катушке индуктивности будет равен
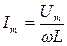
Поделив на 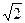 получим
получим
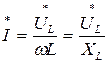
Это закон Ома для цепи с L, где 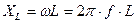 , т.е. пропорционально f и называется индуктивным сопротивлением [Ом]. Очевидно, что при f=0, индуктивное сопротивление катушки постоянному току равно нулю.
, т.е. пропорционально f и называется индуктивным сопротивлением [Ом]. Очевидно, что при f=0, индуктивное сопротивление катушки постоянному току равно нулю.
Комплексное сопротивление цепи с индуктивностью
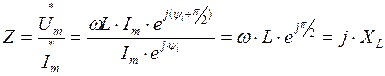
Комплексная проводимость
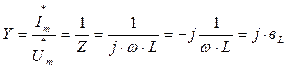 , где
, где
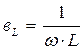 - индуктивная проводимость в [См].
- индуктивная проводимость в [См].
Как видно, комплексные сопротивления и проводимость являются мнимыми величинами, т.е. являются реактивными.
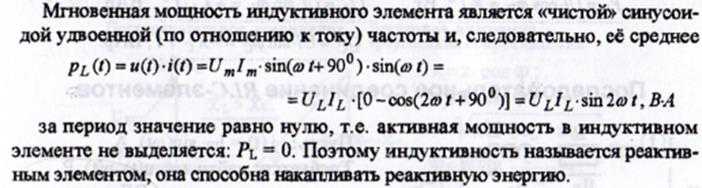
Среднее значение мощности за период
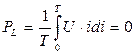
Амплитуда колебаний мощности в цепи с идеальной катушкой индуктивности называется реактивной индуктивной мощностью.
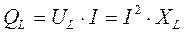
 2015-05-13
2015-05-13 7388
7388
