Согласно закону Ома, сопротивление цепи – это отношение напряжения к току.
Если синусоидальное напряжение
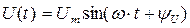 , то ток будет
, то ток будет
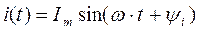 , а сопротивление
, а сопротивление

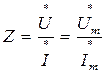 - называется комплексным электрическим сопротивлением и представляет собой закон Ома в комплексной форме.
- называется комплексным электрическим сопротивлением и представляет собой закон Ома в комплексной форме.
Если подставить значения
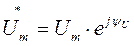 и
и 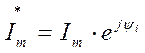 , то получим
, то получим 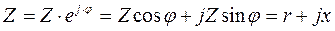 , где
, где
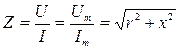 - полное сопротивление.
- полное сопротивление.
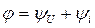 - сдвиг фаз между напряжением и током.
- сдвиг фаз между напряжением и током.
Комплексная проводимость Y может быть представлена в виде
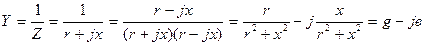
где 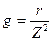 ,
, 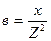 .
.
Зная комплексные сопротивления Z и проводимость Y закон Ома можно записать в форме
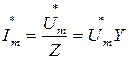 ;
; 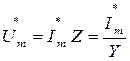 , т.е.
, т.е.
комплексная амплитуда синусоидального тока 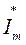 в цепи равна комплексной амплитуде напряжения
в цепи равна комплексной амплитуде напряжения 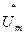 , деленной на комплексное сопротивление Z.
, деленной на комплексное сопротивление Z.
I закон Кирхгофа. Для узла электрической цепи переменного тока алгебраическая сумма мгновенных значений токов в узле равна нулю, т.е.
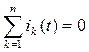 , а в комплексной форме
, а в комплексной форме
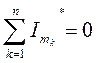 , т.е
, т.е
алгебраическая сумма комплексных амплитуд токов, сходящихся в узловой точке электрической цепи, равна нулю.
Второй закон Кирхгофа для мгновенных значений ЭДС и напряжений записывается в форме
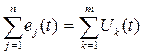 , а в комплексной форме
, а в комплексной форме
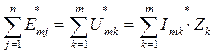 , т.е.
, т.е.
В любом замкнутом контуре электрической цепи переменного тока алгебраическая сумма комплексных амплитуд ЭДС равна сумме комплексных амплитуд напряжений на элементах контура.
Методы расчета цепей постоянного тока вполне применимы к расчету цепей синусоидального тока, если представить все электрические величины в комплексной форме.
Метод расчета. основанный на изображении гармонических функций времени комплексными числами, называют методом комплексных амплитуд.

 2015-05-13
2015-05-13 911
911

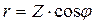 -
-  -
- 






