 С помощью векторных диаграмм можно производить анализ и расчет цепей синусоидального тока. Однако, точность (из-за графического изображения) при этом невелика. Поэтому в электротехнике широко используется представление синусоидальных величин на комплексной плоскости.
С помощью векторных диаграмм можно производить анализ и расчет цепей синусоидального тока. Однако, точность (из-за графического изображения) при этом невелика. Поэтому в электротехнике широко используется представление синусоидальных величин на комплексной плоскости.
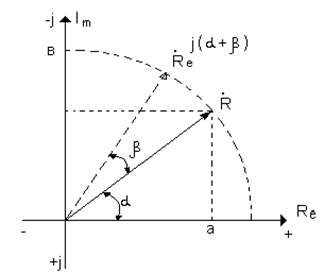
Комплексная плоскость – это прямоугольная система координат, когда на оси абсцисс Re откладываются вещественные, а на оси ординат Im мнимые числа.
Следовательно (общепринято), R e – это действительная часть комплексной функции (времени), а Im – это значение мнимой части комплексной функции (времени).
Комплексное число – это сумма вещественного и мнимого чисел.
Рис 55.
Комплексное число может быть представлено в показательной, тригонометрической и алгебраической формах записи.
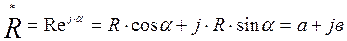 , где
, где
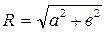 - модуль комплексного числа.
- модуль комплексного числа.
а – вещественная часть комплексного числа.
в – мнимая часть комплексного числа.
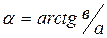 - аргумент комплексного числа, проще – угол между комплексной величиной и ее действительной частью.
- аргумент комплексного числа, проще – угол между комплексной величиной и ее действительной частью.
Таким образом мнимая часть представляет собой синусоидальную функцию аргумента (α) комплексного числа.
При показательной форме записи комплексного числа множитель 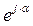 означает поворот вектора
означает поворот вектора 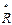 на угол α против часовой стрелки, начиная от +Re и называется оператором поворота. Следовательно, для токо чтобы повернуть вектор
на угол α против часовой стрелки, начиная от +Re и называется оператором поворота. Следовательно, для токо чтобы повернуть вектор 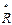 на комплексной плоскости на некоторый угол β достаточно умножить его на ejβ (оператор поворота), т.е.
на комплексной плоскости на некоторый угол β достаточно умножить его на ejβ (оператор поворота), т.е.
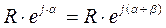
 (рис. 55).
(рис. 55).
Если принять, что 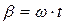 , то оператор поворота
, то оператор поворота 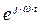 становится оператором вращения. При умножении на оператор вращения (
становится оператором вращения. При умножении на оператор вращения (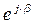 ) некоторого комплексного числа
) некоторого комплексного числа 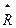 соответствующей этому числу вектор начнет (будет) вращаться на комплексной плоскости со скоростью
соответствующей этому числу вектор начнет (будет) вращаться на комплексной плоскости со скоростью
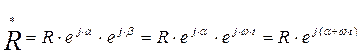
Это выражение учитывает изменение комплексного числа (функции) во времени.
Производная от комплексной функции по времени равна:
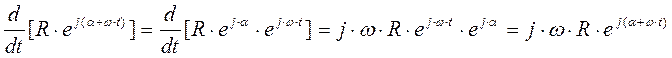
Интеграл такой функции равен:

 Таким образом при дифференцировании комплексной функции ее следует умножить на
Таким образом при дифференцировании комплексной функции ее следует умножить на 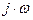 , а при интегрировании – поделить на
, а при интегрировании – поделить на 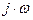 .
.
Два комплексных числа 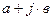 и
и 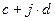 равны, когда а=с и в=d.
равны, когда а=с и в=d.
Два комплексных числа называются сопряженными, если вещественные части равны, а мнимые части также равны, но противоположны по знаку, т.е. функции 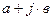 и
и 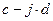 - будут комплексно сопряженными функциями.
- будут комплексно сопряженными функциями.
При умножении комплексных чисел (в показательной форме записи) умножаются модули, а показатели экспонент складываются, т.е.
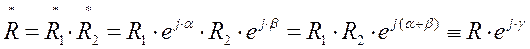
При делении комплексных чисел берется отношение модулей, а показатели экспонент вычитаются, т.е
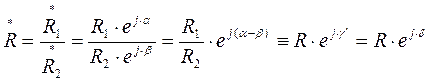
Переменные синусоидальные ток I, напряжение U и ЭДС Е записываются в форме
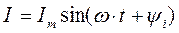 ,
,
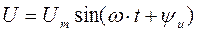 ,
,
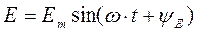 ,
,
а соответствующие им мгновенные значения
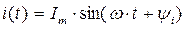 и.т.д.
и.т.д.
Синусоидальная функция на комплексной плоскости представляется вектором, равным
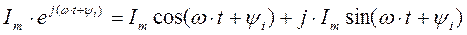
По форме записи видно, что мгновенное значение синусоидальной функции равно мнимой части вектора, вращающегося на комплексной плоскости, т.е. 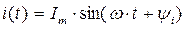 или проекции этого вектора
или проекции этого вектора 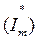 на мнимую ось (ординат).
на мнимую ось (ординат).
Иногда используют формулу записи для мгновенных значений в виде
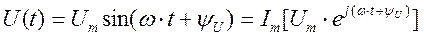
где Im – означает, что от комплексной функции, записанной в квадратных скобках, берется только значение мнимой части.
Постоянную часть (составляющую) в комплексном мгновенном синусоидальным токе, т.е
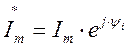 - называют комплексной амплитудой синусоидального тока.
- называют комплексной амплитудой синусоидального тока.
Комплексную величину
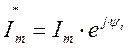 называют комплексным действующим значением синусоидального тока или комплексным током, где
называют комплексным действующим значением синусоидального тока или комплексным током, где
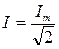
Таким образом комплексный ток 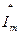 имеет тот же аргумент
имеет тот же аргумент 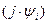 , что и комплексная амплитуда, а модуль меньший, чем у комплексной амплитуды в
, что и комплексная амплитуда, а модуль меньший, чем у комплексной амплитуды в 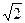 раз.
раз.
Обычно на комплексной плоскости откладываются действующие значения синусоидальных величин.
 2015-05-13
2015-05-13 4133
4133
