2015-05-13
436
В данной балке можно построить эпюры, не определяя опорных реакций, если на всех участках выражения для Qy и Мх составлять, используя нагрузки, расположенные справа от сечения, а левую часть стержня (вместе с неизвестными реакциями) отбрасывать. (К 2.13, К 2.21).
Пронумеруем участки (по направлению). На каждом покажем произвольное сечение, привязав его к правому краю балки (К 2.19).
Записываем аналитические выражения для Qy и Мх (С 2.8, К 2.14, К 2.10). Полу-ченные функции изображаем графически (К 2.16, С 2.9).
1-й участок (0 ≤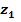 
≤ 2 м)
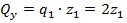(наклонная прямая) (К 2.20)
; 
;
= 
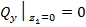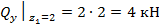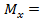
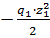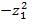(квадратная парабола)
; 
;
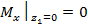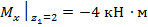Выпуклость параболы - вниз (К 2.30).
Касательная к ней горизонтальна в сечении, где Qy = 0, то есть на краю балки.
Комментарий 2.35 При вычислении значений усилий необходимо указывать сечения, для которых производится подсчет.
В задаче 2.8 указание выполнялось явно.
Например: при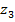 
=2м Мх =…
В задаче 2.9для этого используется значок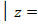 
, который читается как “при”.
Так, выражение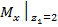 
можно прочитать как “значение Мх при 
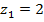м”.
|
|
|
Еще один способ заключается в том, чтобы обозначить все сечения балки буквами: A, B, C, D, E и.т.д.. В этом случае можно, например, записать
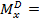, что будет обозначать:
“значение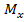 
в сечении D ”
Каждый вправе использовать тот способ указания сечений, который ему нравиться.
2-й участок 2 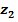м ≤ 
≤ 4 м
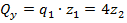(наклонная прямая) (К 2.20, К 2.15)
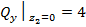кН;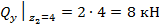 
;
Наклон графика Qy (z) одинаков на 1 - м и 2 - м участках (С 2.15).
= 
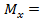
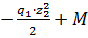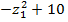(квадратная парабола)
; 
;
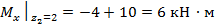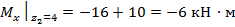Более точно квадратная парабола строится по трем точкам.
Третью точку берем в середине участка.
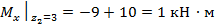
Выпуклость параболы - вниз (К 2.30).
Экстремумов нет (К 2.29).
На стыке 1 -го и 2 -го участков приложен сосредоточенный момент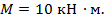 
В силу этого (К 2.33) на эпюре Мх образовался сачок, по величине и направлению совпадающий с внешним моментом.
3-й участок 4 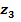м ≤ 
≤ 7 м
Составляя выражения Qy (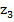
)и Мх (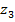) заметим, что теперь справа от сечения оказалась вся нагрузка q1 (равнодействующая q1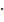 
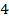м с плечом (
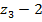) м) и часть нагрузки q2 (равнодействующая q2 (
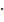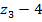)с плечом (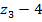)/2).
;
; 
;
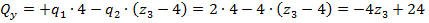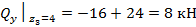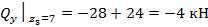Наклонная прямая Qy (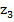)имеет уклон в другую сторону и расположена круче, чем на 1 –м и 2 –м участках, поскольку тангенс угла ее наклона равен нагрузке q2, которая имеет другой знак и больше по величине, чем q1.
=
= 
;
;
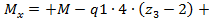
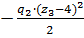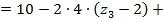
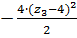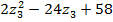
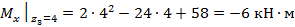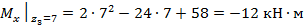На стыке 2 -го и 3 -го участков к балке не приложены сосредоточенные силы и моменты. Поэтому в данном сечении эпюра Мх не имеет разрыва (К 2.33) и не имеет
излома (К 2.32), то есть гладкая. Квадратная парабола волоокостью вверх и имеет экстремум в том сечении, где эпюра Qy пересекает ось (Qy = 0). Для построения параболы в данном случае следует третье значение считать не в середине участка (как на участке 2), а в месте экстремума.
|
|
|
Комментарий 2.36 Экстремальные значения усилий принято вычислять, поскольку часто они являются наибольшими и определяют положение опасного сечения (С 2.10).
Для того, чтобы найти экстремум квадратной функции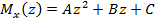 
на некотором участке, следует сначала найти его расположение, то есть положение сечения, в котором Qy (z) обращается в нуль.
Пусть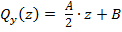 
(C 2.12),
Что следует из формулы (2.6)
Пусть при z =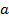 
функция Qy (z) обращается в нуль.
То есть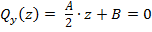 
Откуда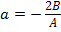 
Подставляем значение 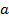в выражение 
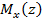получим экстремальное значение момента.
В данном случае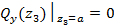 
, то есть
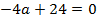, откуда 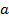= 6 м.
Экстремальное значение 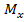равно:
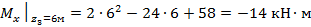
Проводим квадратную параболу через три точки.
Эпюры Qy и Мх построены.
Задача 2.10 Аналитическим способом построить эпюры усилий для балки, изображенной на рис. 2.41 (К 2.34).
