2015-05-13
2119
Тема: «Формирование двумерного массива
по заданному образцу».
Варианты индивидуальных заданий:
В вариантах 1-12 сформировать квадратную матрицу порядка n по заданному образцу.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
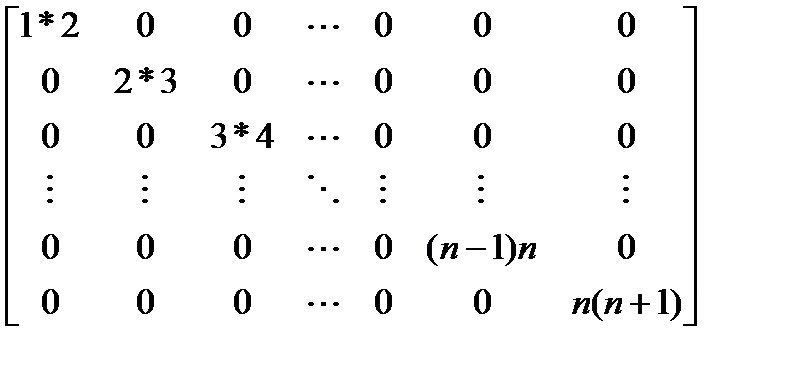
Вариант 5.
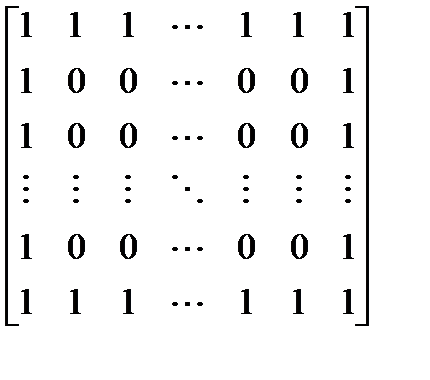
Вариант 6.
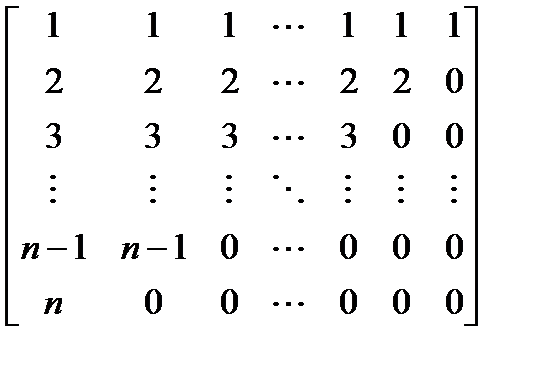
Вариант 7.
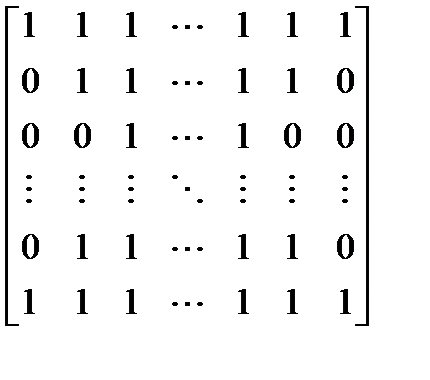
Вариант 8.
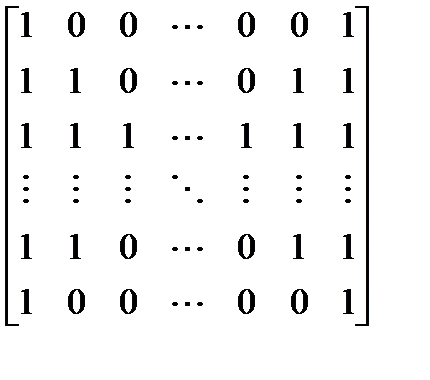
Вариант 9.
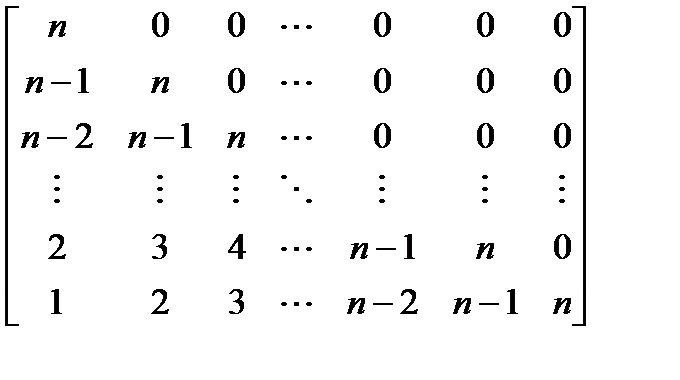
Вариант 10.
Вариант 11.
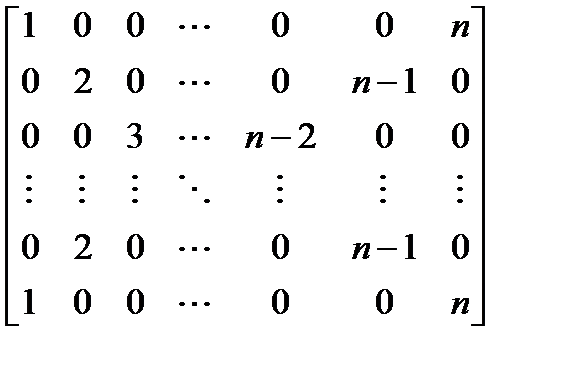
Вариант 12.
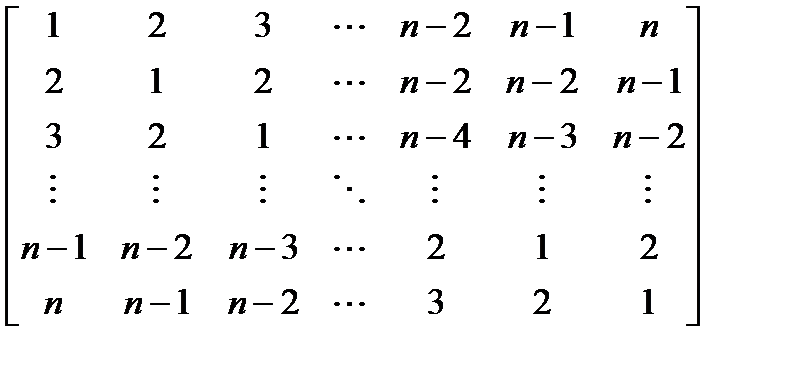
Вариант 13.
Получить матрицу:
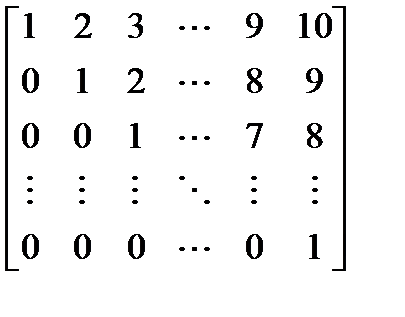
Вариант 14.
Получить матрицу:
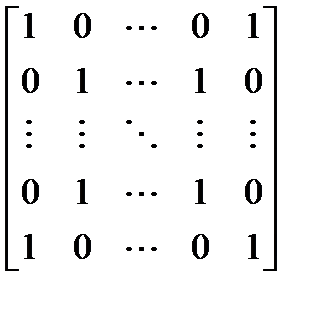
Вариант 15.
Построить квадратную матрицу порядка 2n:
Вариант 16.
Дано х. Получить матрицу порядка n+1:
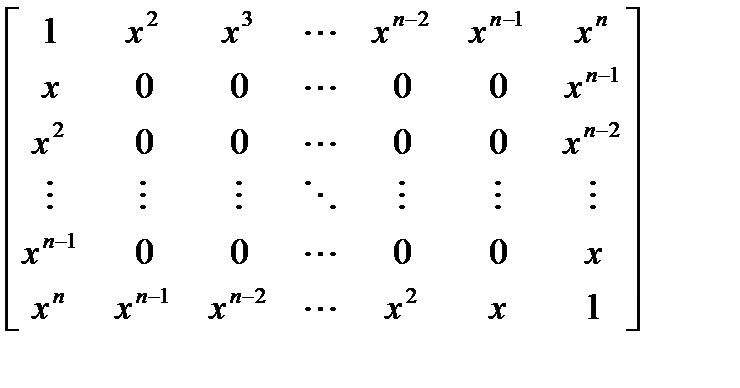
Вариант 17.
Даны действительные числа a1, a2, …, an. Получить квадратную матрицу порядка n:
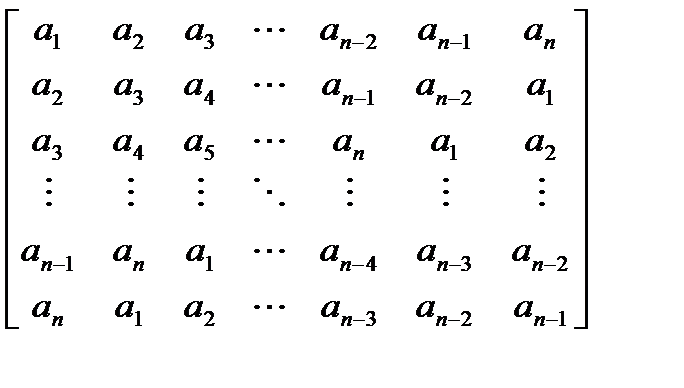
Вариант 18.
Составить программу, которая заполняет квадратную матрицу порядка n числами 1, 2, 3, …, n2 записывая их в нее по спирали. Например, для n=5 получаем следующую матрицу:
Вариант 19.
Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки n*n по часовой стрелке, начиная с блока в левом верхнем углу.
Вариант 20.
Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки n*n крест-накрест.
Вариант 21.
Дан линейный массив x1, x2, …, xn. Получить действительную квадратную матрицу порядка n:
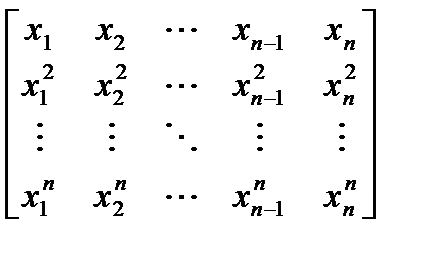
Вариант 24.
Магическим квадратом порядка n называется квадратная матрица размера n*n, составленная из чисел 1, 2,..., n2 так, что суммы по каждому столбцу, каждой строке и каждой из двух больших диагоналей равны между собой. Построить такой квадрат.
Пример магического квадрата порядка 3:
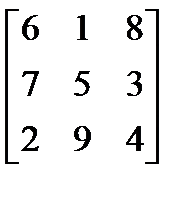
Вариант 22.
Дан линейный массив x1, x2, …, xn. Получить действительную квадратную матрицу порядка n:
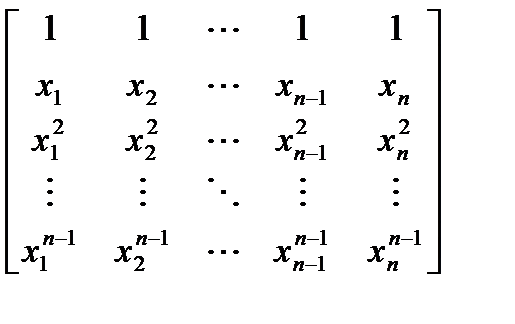
Вариант 23.
Получить квадратную матрицу порядка n:
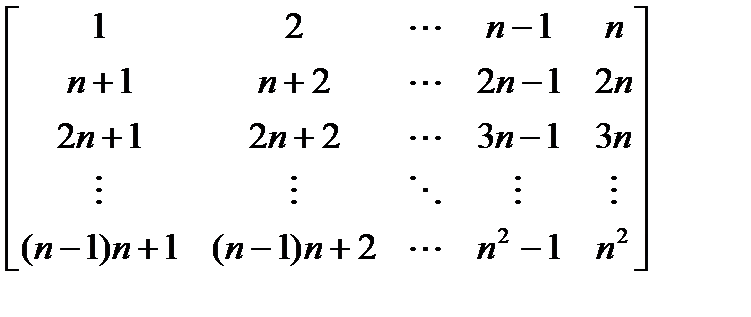
Вариант 25.
Сформировать квадратную матрицу порядка N по правилу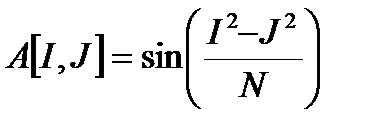 
и подсчитать количество положительных элементов в ней.
