Дан аналоговый сигнал 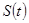 , который имеет сплошной спектр
, который имеет сплошной спектр 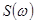
Спектральная плотность 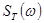 дискретизированного по времени сигнала
дискретизированного по времени сигнала 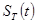 имеет периодическую структуры с периодом нах по оси частот
имеет периодическую структуры с периодом нах по оси частот 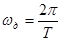 , т.е. спектр аналогового сигнала периодически повторяется.
, т.е. спектр аналогового сигнала периодически повторяется.
Спектр дискретизированного сигнала по времени (2) будет определяться следующим выражением
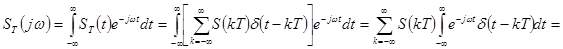
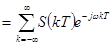 (3)
(3)
Если количество выборок конечно 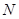 и сигнал существует при
и сигнал существует при 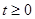 , то сумма (3) становится конечной.
, то сумма (3) становится конечной. 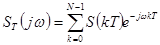 (4)
(4)
где 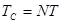 - длительность сигнала;
- длительность сигнала; 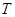 - период дискретизации;
- период дискретизации; 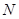 - количество выборок.
- количество выборок.
Для осуществления цифровой обработки требуется дискретизация сигнала не только во временной, но и в частотной области. Это означает, что сплошной спектр 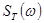 должен быть представлен совокупностью своих значений
должен быть представлен совокупностью своих значений 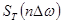 на дискретных частотах
на дискретных частотах 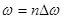 . Такой спектр, получается из сплошного
. Такой спектр, получается из сплошного 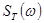 при периодическом повторении последовательности
при периодическом повторении последовательности 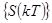 с периодом
с периодом 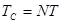 . Интервал между соседними спектральными линиями
. Интервал между соседними спектральными линиями 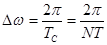 (5)
(5)
Подставляя 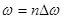 в выражение (4)
в выражение (4) 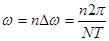 получаем
получаем
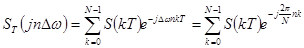 , где
, где 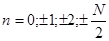 при чётном
при чётном 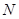 (6)
(6)
Полученное выражение (6) называют дискретным преобразованием Фурье (ДПФ). Аргументы 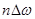 и
и 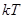 обычно называются просто
обычно называются просто 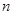 и
и 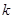 . Поэтому ДПФ можно записать
. Поэтому ДПФ можно записать
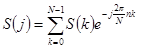 , где
, где 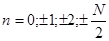 (7)
(7)
в пределах одного периода 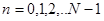 . Выражение (6) трактовать, как алгоритм вычисления спектральных коэффициентов
. Выражение (6) трактовать, как алгоритм вычисления спектральных коэффициентов 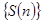 по заданным временным отсчётам
по заданным временным отсчётам 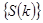 . Если
. Если 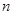 велико, то реализовать (6) очень сложно.
велико, то реализовать (6) очень сложно.
Существует алгоритм быстрого преобразования Фурье – реализован в микросхемах.
Используя дуальность прямого и обратного преобразования Фурье можно, основываясь на выражении (7) получить выражение для ОДПФ
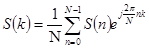 , где
, где 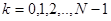 (8)
(8)
Обратное дискретное преобразование Фурье (ОДПФ).
Вывод. Дискретизированному сигналу 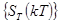 , где
, где 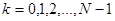 , соответствует сложный спектр
, соответствует сложный спектр 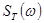 с периодической структурой. Свойства непрерывных преобразований Фурье распространяются также и на ДПФ
с периодической структурой. Свойства непрерывных преобразований Фурье распространяются также и на ДПФ
Дискретизированному спектру 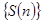 соответствует периодическая последовательность сигналов
соответствует периодическая последовательность сигналов 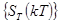 повторяемых с периодом
повторяемых с периодом 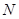 .
.
Дискретное преобразование Лапласа 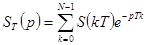 (9)
(9)
Неудобство функции 5,6,7,3 является наличие множителя 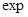 , что существенно затрудняет анализ. Его можно упростить при переходе к новой переменной
, что существенно затрудняет анализ. Его можно упростить при переходе к новой переменной 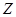 связанной с
связанной с 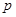 следующим соотношением
следующим соотношением 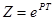 ;
; 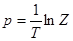
При такой замене указанные функции от 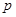 преобразуются рациональные функции от переменной
преобразуются рациональные функции от переменной 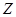
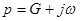 ;
; 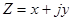
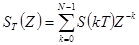 (10)
(10)
прямое 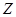 - преобразование (одностороннее).
- преобразование (одностороннее).
Некоторые свойства 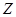 - преобразования.
- преобразования.
Преобразование плоскости 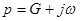 в плоскость
в плоскость 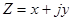 можно осуществить с помощью следующих соотношений, связывающих координаты какой-либо точки
можно осуществить с помощью следующих соотношений, связывающих координаты какой-либо точки 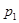 на плоскости
на плоскости 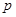 с координатами
с координатами 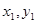 , соответствующей точке
, соответствующей точке 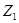 на плоскости
на плоскости 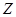 .
.
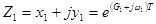
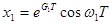
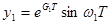 .
.
В полярных координатах на плоскости 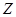
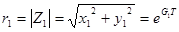 ,
, 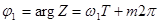 .
.
Рассмотрим отображение некоторых характерных точек и областей из 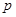 -плоскости на
-плоскости на 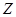 - плоскость.
- плоскость.
а) Точка 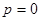 переходит в точку
переходит в точку 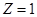 на вещественной оси
на вещественной оси 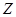 - плоскости.
- плоскости.
б) при движении точки 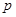 - плоскости вдоль оси
- плоскости вдоль оси 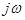 (т.е.
(т.е. 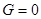 ) в пределах
) в пределах 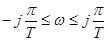 соответствующая ей точка
соответствующая ей точка 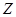 - плоскости описывает окружность единичного радиуса. Один полный оборот радиуса-вектора соответствует изменению частоты
- плоскости описывает окружность единичного радиуса. Один полный оборот радиуса-вектора соответствует изменению частоты 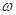 в интервале
в интервале 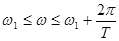
в) Левая полуплоскость 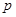 внутри полосы
внутри полосы 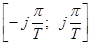 отображается внутрь единичного круга на плоскости
отображается внутрь единичного круга на плоскости 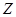 .
.
г) При движении точки 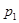 вдоль оси
вдоль оси 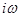 в пределах от
в пределах от 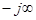 до
до 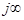 точка
точка 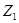 описывает бесконечно большое число окружностей. Внутри этой полосы левая полуплоскость отображается внутрь единичного круга. Все параллельные полосы такой же ширины соответствуют этому же кругу.
описывает бесконечно большое число окружностей. Внутри этой полосы левая полуплоскость отображается внутрь единичного круга. Все параллельные полосы такой же ширины соответствуют этому же кругу.
д) Правая полуплоскость 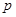 преобразует во всю
преобразует во всю 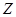 - плоскость, исключая единичный круг.
- плоскость, исключая единичный круг.
На основании формулы (1) можно непосредственно найти 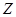 преобразования дискретных сигналов если этот ряд сходится.
преобразования дискретных сигналов если этот ряд сходится.
Пример. Простейшему дискретному сигналу с единственным отсчётом 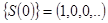 соответствует
соответствует 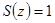 .
.
2. 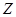 - преобразование дискретной функции Хевисайда.
- преобразование дискретной функции Хевисайда.
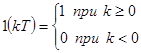
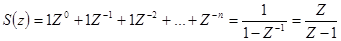
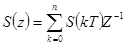
Функция сходится при 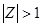
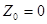 , радиус сходимости
, радиус сходимости 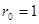 ,
, 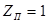 - полюс.
- полюс.
 2015-05-13
2015-05-13 1176
1176
