Рассмотрим линейный АД на входе которого с УПЧ действует несущее колебание, а также узкополосный шум: 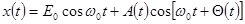 (1)
(1)
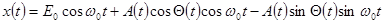
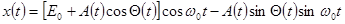 (2)
(2)
Квадратурные слагаемые узкополосного процесса.
Сумма двух ВЧ процессов 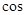 случайными амплитудами.
случайными амплитудами.
Преобразуем выражение (2) 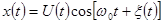 (3)
(3)
где 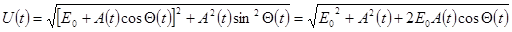 (4)
(4)
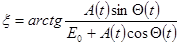 (5)
(5)
И так можно рассматривать, что на входе АД действует узкополосный шум со случайной огибающей 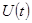 и фазой
и фазой 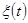 . При анализе воздействия колебания со случайной амплитудой и фазой на АД статистическими характеристиками фазы
. При анализе воздействия колебания со случайной амплитудой и фазой на АД статистическими характеристиками фазы 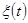 можно не интересоваться. Основное значение имеет плотность вероятности
можно не интересоваться. Основное значение имеет плотность вероятности 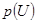 огибающей
огибающей 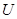 , определяется по формуле:
, определяется по формуле:
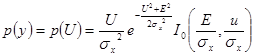 (6)
(6)
Определяемая формулой (6) функция называется обобщённой функцией Рэлея (или закон Райса).
Где 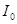 - есть функция Бесселя комплексного аргумента (модифицированная функция).
- есть функция Бесселя комплексного аргумента (модифицированная функция).
Рассмотрим как будет изменяться закон распределения сигнала на выходе АД в зависимости от соотношения 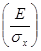 на входе.
на входе.
При 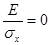 отсутствует полезный сигнал, закон распределения выходного сигнала рэлеевский. В другом крайнем случае, когда амплитуда сигнала
отсутствует полезный сигнал, закон распределения выходного сигнала рэлеевский. В другом крайнем случае, когда амплитуда сигнала 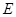 велика по сравнению с
велика по сравнению с 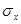 кривая
кривая 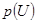 близка к гаусовской кривой со средним значением
близка к гаусовской кривой со средним значением 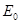 .
.
Зная закон распределения случайного процесса на входе АД (6) можно определить математическое ожидание, дисперсию и средний квадрат. Отношение сигнал/помеха – это отношение мощности сигнала к мощности флуктуаций. 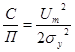 (7)
(7)
Где 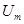 - амплитуда гармонического сигнала,
- амплитуда гармонического сигнала, 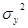 - мощность флуктуаций шума.
- мощность флуктуаций шума.
Рассмотрим два случая:
1) в случае сильного сигнала 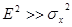 , тогда
, тогда 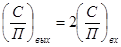 (8), т.е. сильный сигнал практически подавляет помеху.
(8), т.е. сильный сигнал практически подавляет помеху.
2) если 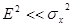 , то
, то 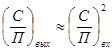 (9), при слабом сигнале в квадратичном детекторе имеет место подавление сигнала.
(9), при слабом сигнале в квадратичном детекторе имеет место подавление сигнала.
 2015-05-13
2015-05-13 752
752








