Задача № 17

Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 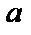и средним квадратическим отклонением 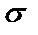. Годными считаются детали, для которых отклонение от номинала лежит в интервале 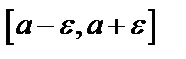. Требуется:

1) составить функцию плотности вероятности;

2) найти вероятность того, что при выборе наудачу 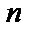деталей отклонение каждой из них попадет в интервал .

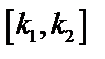замечание. В п.2. пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.

Вариант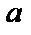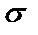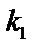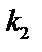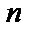
			1,29	2,25
			1,718	3,524
	-1		-6,185	-0,375
			-6,185	-0,375
	-2	0,2	-2,526	0,771
		0,5	-2,135	-1,923
	-1		-1,77	0,35
			-0,257	1,282
			0,625	4,111
	-2		-2	-0,718
	-2		-3,684	2,514
	-1		-1,375	2,111
			-6,58	0,5
	-1	0,4	-1,154	1,7
			0,926	3,25
			-0,028	6,028
			-3,1	9,62
	-1		-2,282	-0,476
				3,564
			-0,786	1,263
	-1		-1,842	-0,743
			-3,945	1,375
	-3		-4,037	-2,875
		0,05	1,9738	2,0241
	-10		-10	-4,872
			-4,05	2,31
			-5,41	3,62
				9,296
	-1		-6,14	24,64
			-1,85	8,75

Приложение I