Комплексным числом 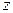 называется выражение вида
называется выражение вида 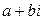 , где
, где 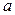 и
и 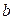 - действительные числа,
- действительные числа, 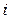 - мнимая единица, определяемая равенством
- мнимая единица, определяемая равенством 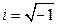 или
или 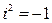 :
:
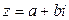 ; (1.1)
; (1.1)
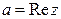 называется действительной или вещественной частью комплексного числа
называется действительной или вещественной частью комплексного числа 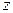 ;
; 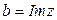 называется его мнимой частью. В технической литературе применяется также обозначение
называется его мнимой частью. В технической литературе применяется также обозначение 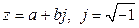 .
.
Если 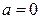 , то число
, то число 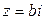 называется чисто мнимым; если же
называется чисто мнимым; если же 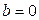 , то
, то 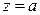 , т.е. получаем действительное число. Комплексные числа
, т.е. получаем действительное число. Комплексные числа 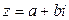 и
и 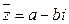 называются сопряженными.
называются сопряженными.
► Приведите пример комплексного числа, чисто мнимого числа, действительного числа.
► Запишите числа, сопряженные к 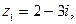
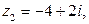
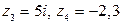 .
.
Два комплексных числа 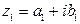 и
и 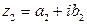 называются равными, если
называются равными, если 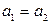 ,
, 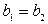 , т.е. если равны их действительные и мнимые части. Комплексное число
, т.е. если равны их действительные и мнимые части. Комплексное число 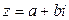 равно нулю тогда и только тогда, когда
равно нулю тогда и только тогда, когда 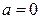 и
и 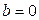 . Выражение (1.1) называется алгебраической формой комплексного числа.
. Выражение (1.1) называется алгебраической формой комплексного числа.
Арифметические действия с комплексными числами в алгебраической форме осуществляются следующим образом.
Суммой (разностью) комплексных чисел 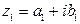 и
и 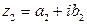 называется число
называется число 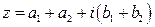 (
(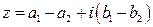 ).
).
Произведением комплексных чисел 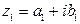 и
и 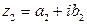 называется число
называется число 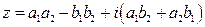 .
.
Частным от деления комплексного числа 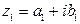 на комплексное число
на комплексное число 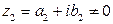 называется число
называется число
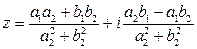 .
.
► Даны два комплексных числа 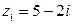 и
и 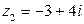 . Укажите их действительные и мнимые части. Найдите их сумму, разность, произведение и частное и запишите сопряженные к ним комплексные числа.
. Укажите их действительные и мнимые части. Найдите их сумму, разность, произведение и частное и запишите сопряженные к ним комплексные числа.
Отметим, что действия с комплексными числами в алгебраической форме выполняются как с многочленами с учетом того, что 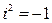 .
.
Пример 1.1. Решить уравнение 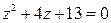 и проверить правильность полученного результата.
и проверить правильность полученного результата.
Решение. 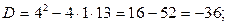
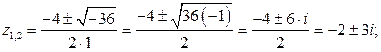
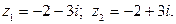
Проверка.
1) 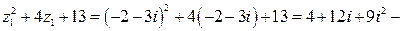
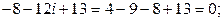
2) 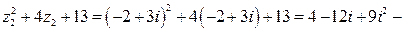
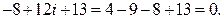
Следовательно, задача решена верно.
Заметим: если дискриминант квадратного уравнения отрицательный, то оно имеет комплексные корни, причем корни являются сопряженными, как и показывает предыдущий пример.
Комплексное число 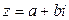 можно изобразить точкой
можно изобразить точкой 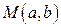 с координатами
с координатами 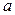 и
и 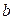 или вектором
или вектором 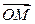 также с координатами
также с координатами 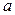 и
и 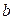 .
.
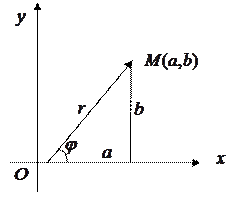 |
Рис. 1.1.
 2015-05-13
2015-05-13 398
398








