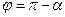Обозначим через 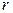 и
и 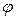 полярные координаты точки
полярные координаты точки 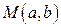 , считая начало координат полюсом, а положительное направление оси
, считая начало координат полюсом, а положительное направление оси 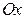 – полярной осью. Тогда
– полярной осью. Тогда
(рис. 1) можно записать
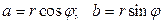
и
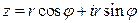
или
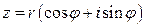 (1.2)
(1.2)
Выражение, стоящее справа в формуле (1.2), называется тригонометрической формой записи комплексного числа; 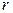 называется модулем комплексного числа, а
называется модулем комплексного числа, а 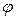 – его аргументом; они обозначаются следующим образом:
– его аргументом; они обозначаются следующим образом:
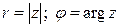 ,
,
при этом 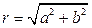 ,
, 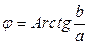 .
.
Аргумент комплексного числа считается положительным, если он отсчитывается от положительного направления оси 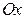 против часовой стрелки, и отрицательным, если он отсчитывается по часовой стрелке. Аргумент комплексного числа определяется не однозначно, а с точностью до слагаемого
против часовой стрелки, и отрицательным, если он отсчитывается по часовой стрелке. Аргумент комплексного числа определяется не однозначно, а с точностью до слагаемого 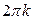 , где
, где 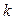 - любое целое число. Обычно используется главное значение аргумента
- любое целое число. Обычно используется главное значение аргумента 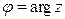 , определяемое дополнительными условиями
, определяемое дополнительными условиями 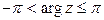 или
или 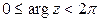 . В дальнейшем, для определенности, будем считать, что
. В дальнейшем, для определенности, будем считать, что 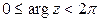 . Если воспользоваться формулой Эйлера
. Если воспользоваться формулой Эйлера
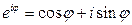 ,
,
то из тригонометрической формы (1.2) записи комплексного числа получаем показательную форму записи комплексного числа
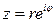
Тригонометрическая и показательная формы записи комплексного числа особенно удобны при умножении, делении, возведении в степень комплексных чисел и извлечении корня из комплексного числа.
Пусть 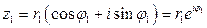 ,
,
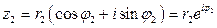 .
.
Тогда
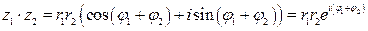 ,
,
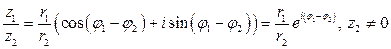 .
.
► Найти действительную и мнимую части комплексного числа
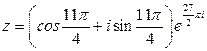 .
.
Ответ: 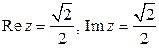 .
.
Возведение в степень комплексного числа 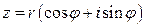 и извлечение корня из него производится по формуле Муавра:
и извлечение корня из него производится по формуле Муавра:
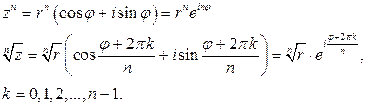 (1.3)
(1.3)
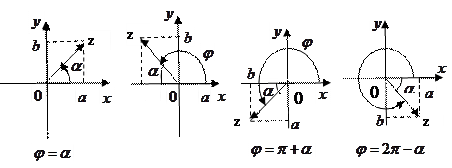 Замечание. При переходе от алгебраической формы записи комплексного числа к тригонометрической удобно пользоваться следующим правилом: обозначим
Замечание. При переходе от алгебраической формы записи комплексного числа к тригонометрической удобно пользоваться следующим правилом: обозначим 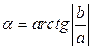 ; тогда
; тогда 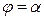 , если комплексное число находится в первой четверти;
, если комплексное число находится в первой четверти; 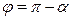 для комплексного числа
для комплексного числа 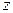 , находящегося во второй четверти; для комплексных чисел, находящихся в третьей и четвертой четвертях, соответственно
, находящегося во второй четверти; для комплексных чисел, находящихся в третьей и четвертой четвертях, соответственно 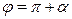 и
и 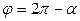 (рис. 2).
(рис. 2).
| |||||
 | |||||
|
Рис. 1.2.
► Изобразите графически комплексные числа 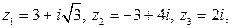
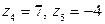 и вычислите их модули и аргументы.
и вычислите их модули и аргументы.
Пример 1.2. Дано: 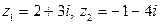 . Найти:
. Найти: 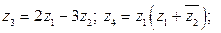
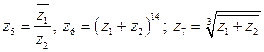 .
.
 2015-05-13
2015-05-13 1273
1273