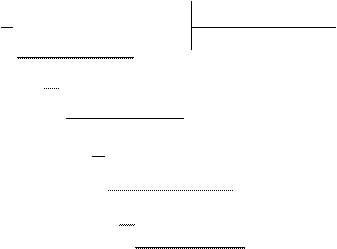
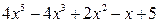
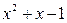
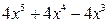
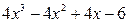
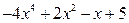
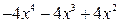
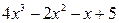
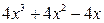
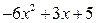
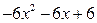
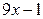
Операция деления начинается с деления старших членов делимого и делителя: 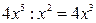 . Результат
. Результат 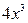 записываем в частное; умножаем делитель на
записываем в частное; умножаем делитель на 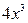 и полученный результат
и полученный результат 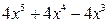 вычитаем из делимого. Получаем первый остаток:
вычитаем из делимого. Получаем первый остаток: 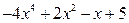 . Далее действия повторяются, только в качестве делимого выступает первый остаток: его старший член делим на старший член делителя:
. Далее действия повторяются, только в качестве делимого выступает первый остаток: его старший член делим на старший член делителя: 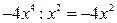 , дописываем результат деления
, дописываем результат деления 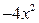 в частное, умножаем делитель на
в частное, умножаем делитель на 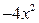 и результат умножения
и результат умножения 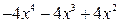 вычитаем из первого остатка, получая при этом второй остаток
вычитаем из первого остатка, получая при этом второй остаток 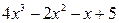 . Описанные действия повторяются до тех пор, пока степень полинома, который получается в остатке, не станет меньше степени делителя, либо остаток окажется равным нулю. В приведенном примере деление закончилось, когда остаток стал равным
. Описанные действия повторяются до тех пор, пока степень полинома, который получается в остатке, не станет меньше степени делителя, либо остаток окажется равным нулю. В приведенном примере деление закончилось, когда остаток стал равным 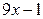 , т.е полиномом первой степени, а делителем является полином второй степени. Результат деления можно записать следующим образом:
, т.е полиномом первой степени, а делителем является полином второй степени. Результат деления можно записать следующим образом:
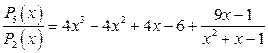
или
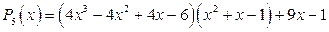 .
.
► Разделите многочлен 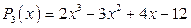 на многочлен
на многочлен 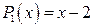 .
.
Важную роль в теории многочленов играет теорема Безу: остаток от деления многочлена 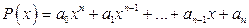 на двучлен
на двучлен 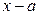 равен
равен 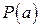 .
.
Следствие: число 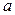 является корнем многочлена
является корнем многочлена 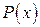 тогда и только тогда, когда он делится без остатка на двучлен
тогда и только тогда, когда он делится без остатка на двучлен 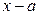 и, следовательно, представляется в виде произведения
и, следовательно, представляется в виде произведения 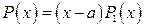 ,
,
где 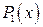 – многочлен степени
– многочлен степени 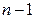 .
.
Основная теорема алгебры гласит: всякая целая рациональная функция 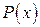 имеет по крайней мере один корень, действительный или комплексный.
имеет по крайней мере один корень, действительный или комплексный.
Пользуясь этой теоремой, легко доказать утверждение: всякий многочлен 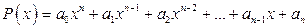 степени
степени 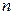 можно представить в виде
можно представить в виде
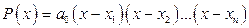 . (1.4)
. (1.4)
Из разложения (1.4) следует, что 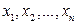 суть корни многочлена
суть корни многочлена 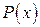 . Из этого же разложения вытекает, что многочлен степени
. Из этого же разложения вытекает, что многочлен степени 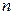 имеет ровно
имеет ровно 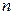 корней (действительных или комплексных).
корней (действительных или комплексных).
Значения этих корней связаны с коэффициентами многочлена 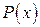 (уравнения
(уравнения 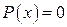 ) следующими формулами Виста (если
) следующими формулами Виста (если 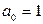 ):
):
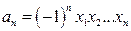 ,
,
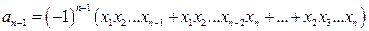 ,
,
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -,
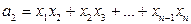 ,
,
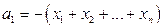 .
.
В частном случае, для приведенного квадратного уравнения 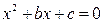 формулы Виста принимают вид
формулы Виста принимают вид 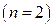 :
:
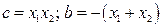 или
или 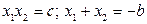 , т.е. произведение корней равно свободному члену, а сумма корней равна коэффициенту при
, т.е. произведение корней равно свободному члену, а сумма корней равна коэффициенту при 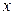 с обратным знаком.
с обратным знаком.
►Разложить многочлен 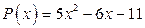 на линейные множители.
на линейные множители.
Если в разложении (1.4) некоторые линейные множители окажутся одинаковыми, то их можно объединить, и тогда разложение многочлена на множители будет иметь вид
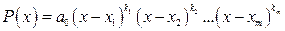 ,
,
при этом 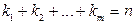 . В этом случае корень
. В этом случае корень 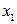 называется корнем кратности
называется корнем кратности 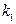 или
или 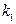 - кратным корнем,
- кратным корнем, 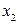 - корнем кратности
- корнем кратности 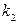 и т.д.
и т.д.
Имеет место следующее утверждение: если 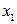 является корнем многочлена
является корнем многочлена 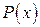 кратности
кратности 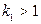 , то он является корнем кратности
, то он является корнем кратности 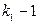 производной
производной 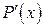 , корнем кратности
, корнем кратности 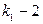 производной второго порядка
производной второго порядка 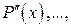 корнем кратности 1 (простым корнем) производной
корнем кратности 1 (простым корнем) производной 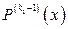 и не является корнем производной
и не является корнем производной 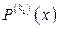 , т.е.
, т.е. 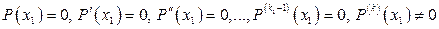 .
.
Справедливо следующее утверждение: если число 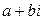 является корнем многочлена
является корнем многочлена 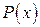 с действительными коэффициентами, то и число
с действительными коэффициентами, то и число 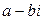 также является его корнем.
также является его корнем.
Из этого утверждения следует: многочлен с действительными коэффициентами разлагается на множители с действительными коэффициентами первой и второй степени соответствующей кратности, т.е. 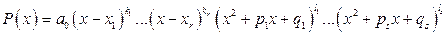 ;
;
здесь 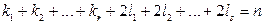 .
.
Пример 1.5. Разложить на простейшие (линейные) множители многочлен 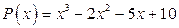 .
.
Решение. Для разложения многочлена на множители достаточно знать его корни. Известно, что любой целый корень приведенного многочлена (со старшим коэффициентом равным 1) с целыми коэффициентами является делителем его свободного члена. Следовательно, если заданный многочлен имеет целые корни, то они являются делителями 10, т.е. находятся в множестве чисел 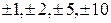 .
.
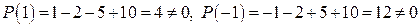 ,
,
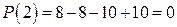 , следовательно
, следовательно 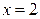 является корнем заданного многочлена:
является корнем заданного многочлена: 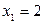 . Разделим
. Разделим 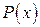 на
на 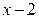 :
:



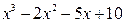
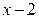

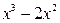
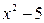
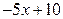

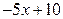
Таким образом
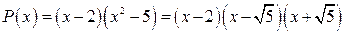 .
.
Ответ: 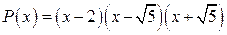 .
.
Пример 1.6. Разложить на простейшие множители с действительными коэффициентами многочлен 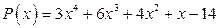 .
.
Решение. 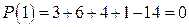 , т.е. первый корень
, т.е. первый корень 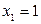 . Разделив
. Разделив 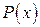 на
на 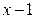 , получаем
, получаем 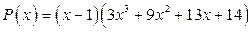 .
.
Обозначим 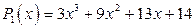
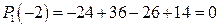 , следовательно, второй корень
, следовательно, второй корень 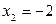 . Разделим
. Разделим 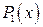 на
на 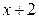 и получим:
и получим:
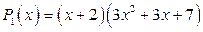 , т.е.
, т.е.
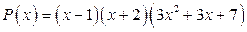 .
.
Найдем теперь корни квадратного трехчлена 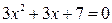 .
.
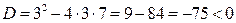 . Следовательно, многочлен
. Следовательно, многочлен 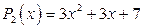 имеет комплексные корни и поэтому на линейные множители с действительными коэффициентами не разлагается.
имеет комплексные корни и поэтому на линейные множители с действительными коэффициентами не разлагается.
Ответ: 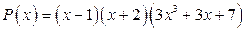
 2015-05-13
2015-05-13 597
597








