Функция 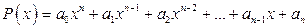 , где
, где 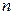 – целое неотрицательное число, коэффициенты
– целое неотрицательное число, коэффициенты 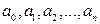 – действительные или комплексные числа, называется многочленом (полиномом) или целой рациональной функцией от
– действительные или комплексные числа, называется многочленом (полиномом) или целой рациональной функцией от 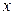 . Число
. Число 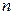 называется степенью многочлена. Независимая переменная
называется степенью многочлена. Независимая переменная 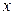 может принимать как действительные, так и комплексные значения. Корнем или нулем многочлена
может принимать как действительные, так и комплексные значения. Корнем или нулем многочлена 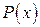 называется такое значение
называется такое значение 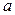 переменной
переменной 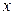 , при котором многочлен обращается в ноль, т.е.
, при котором многочлен обращается в ноль, т.е. 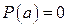 . Корни многочлена связаны с его коэффициентами формулами Виета.
. Корни многочлена связаны с его коэффициентами формулами Виета.
Многочлены можно складывать, вычитать, умножать и делить с остатком или без остатка. Деление многочленов выполняется по правилу, аналогичному правилу деления чисел.
Пример 1.4. Разделить многочлен 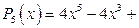
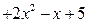 на многочлен
на многочлен 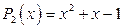 .
.
 2015-05-13
2015-05-13 356
356








