Лабораторная работа №12. Маятник Максвелла

Цель работы - ознакомление с плоским движением твердого тела на примере движения маятника Максвелла.

Лабораторная установка « маятник Максвелла» входит в состав комплекса приборов «Физические основы механики». Общий вид показан на рис. 3. На платформе прибора (1) установлен электронный блок (2), и вертикальная колонна (5). На колонне установлены два кронштейна: верхний (6) и нижний (11). На верхнем кронштейне установлены электромагнит (9), фотоэлектрический датчик (7) и вороток (8) для регулирования длины нитей, а на нижнем закреплен второй фотоэлектрический датчик (3). Положение нижнего кронштейна можно менять и фиксировать на любой высоте.

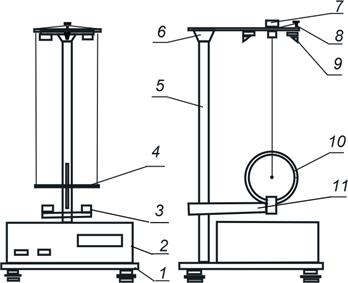
Рис. 3. Лабораторная установка «Маятник Максвелла».

Маятник Максвелла состоит из тонкого металлического стержня (4) с симметрично укрепленным на нем диском (10). К концам стержня прикреплена крепкая капроновая нить, длину которой можно регулировать с помощью воротка (8). Нить пропущена через отверстия в верхнем штативе. На диск маятника надевают одно из сменных колец, затем тщательно, виток к витку, на стержень наматывают нити, от его концов к диску. Их длина измеряется по миллиметровой шкале колонны по красному указателю, помещенному на оптической оси нижнего оптического датчика. При нажатии кнопки «СБРОС» показания таймера обнуляются и включается электромагнит. Он удерживает верхнем положении маятник. Если нажать кнопку «ПУСК», размыкается цепь электромагнита и маятник начинает двигаться под действием силы тяжести поступательно вниз и, одновременно, вращательно вокруг оси симметрии стержня. Когда нити будут полностью размотаны, в нижней точке, угловая скорость вращения маятника будет максимальной, и тогда нити будут наматываться на стержень снова, а маятник станет подниматься вверх, замедляясь. Двигаясь равнозамедленно вверх, маятник достигнет наивысшей точки, остановится, и начнет снова движение вниз и т. д. Диск со стержнем совершает попеременные перемещения вверх-вниз, это похоже на движение маятника, отсюда и название «маятник Максвелла». Каждый цикл движения маятника Максвелла состоит из трех стадий: спуска, рывка и подъема вверх. Схематически график изменения скорости оси маятника при его движении имеет вид, изображенный на рисунке 4. На интервале времени 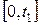маятник движется равноускоренно, затем кинетическая энергия поступательного движения маятника переходит в потенциальную энергию деформации нити, происходит рывок, в результате которого нить сначала растягивается до максимального удлинения, а затем (на промежутке времени 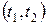), начинает сокращаться, тогда скорость маятника меняет знак, и, затем, маятник движется вверх в течение времени .

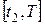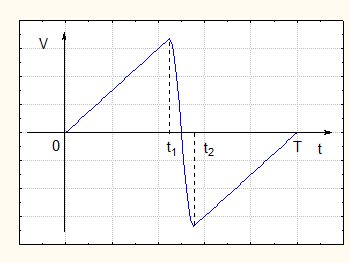Рис. 4. Три стадии движения маятника Максвелла.

Как видно из рисунка 4, время спуска и подъема маятника во много раз превышает время рывка. В течение спуска и поднятия на маятник действуют сила тяжести, сила упругости нитей и силы трения и сопротивления воздуха. Эти силы не изменяются во времени. Во время удара кратковременно действует сила упругости, которая появляется в результате дополнительного растяжения нитей в момент остановки. Эта сила резко нарастает и убывает во времени.

Кинетическая энергия маятника Максвелла состоит из кинетической энергии поступательного и вращательного движения. Во время рывка кинетическая энергия поступательного движения переходит в потенциальную энергию деформации нитей, а кинетическая энергия вращательного движения остается у маятника и заставляет его подниматься вверх.

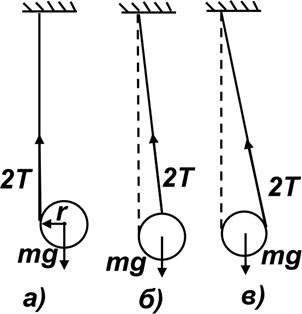
Рис. 5. Три стадии движения маятника Максвелла: а) спуск, б) рывок, в) подъем.

Вывод полного аналитического решения для всего цикла движения маятника не является задачей данной работы. Мы рассмотрим стадии движения по отдельности в упрощенном виде. Поскольку движение происходит под действием силы тяжести и силы натяжения нитей, то движение маятника без раскачивания возможно только, если нити находятся в вертикальной плоскости. На рисунке 5 показаны положения маятника, характерные для его раскручивания, удара и подъема. Видно, что максимальный угол отклонения нити от вертикали связан с радиусом стержня и длиной нити h: 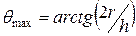. Поэтому силы упругости нитей не всегда направлены вертикально, а имеют во время рывка и подъема горизонтальную составляющую, которая приводит к колебаниям маятника, показанным на рисунке. Ею, как и колебаниями, мы будем пренебрегать.

Теория эксперимента: движение маятника Максвелла рассмотрим как поступательное движение его центра масс в плоскости, проходящей через диск, и вращение стержня с диском относительно оси симметрии. Это позволит нам применить теорему о движении центра масс и уравнение моментов.

Если не учитывать силу трения маятника о воздух и отклонение нитей от вертикали, то система уравнений для первой и третьей стадий движения будут совпадать и иметь вид:

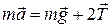, (1)

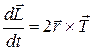. (2)

Здесь m – масса маятника, 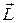– момент импульса диска со стержнем относительно их общей оси симметрии, 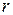– радиус стержня маятника, 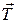– сила натяжения одной нити, 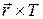– момент силы упругости одной нити.

В качестве положительного направления движения выберем направление сверху вниз, и учтем, что 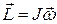, тогда уравнения (1) и (2) примут вид:

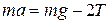, (3)

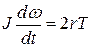. (4)

Между ускорением a поступательного и угловым ускорением вращательного движения 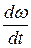существует связь:

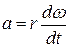. (5)

Из уравнений (4) и (5) следует, что

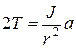, (6)

Подставим выражение для силы упругости нитей в (3), получим формулу для ускорения:

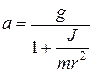. (7)

Ускорение a будет направлено вниз как на первой, так и на третьей стадии движения. Начальная скорость центра масс маятника при опускании равна нулю, а в начале его подъема она максимальна. Из уравнений (3) и (6) получаем формулу для момента инерции:

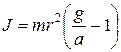. (8)

Двигаясь равноускоренно, маятник преодолевает расстояние h за время t:

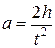. (9)

С учетом (9) момент инерции можно рассчитать, зная пройденное маятником на первой стадии расстояние и время спуска:

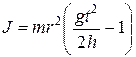. (10)

В лабораторной работе используется маятник Максвелла со сменными кольцами, имеющими внутренний радиус 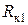и внешний 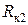. Зная размеры и массы стержня, диска и колец, можно рассчитать теоретическое значение момента инерции маятника Максвелла. Без кольца он складывается из момента инерции стержня и диска:

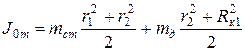, (11)

Момент инерции кольца равен:

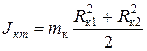. (12)

Здесь m_ст – масса стержня, m_д – масса диска, m_к – масса кольца, r₁ – внутренний радиус кольца, r₂ – внешний радиус стержня, который равен внутреннему радиусу диска, а внешний радиус диска равен внутреннему радиусу кольца 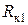. 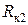– внешний радиус кольца.

Скорость спуска центра масс маятника непосредственно перед ударом:

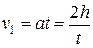, (13)

После удара маятника движется вверх равнозамедленно с ускорением а, направленным так же вниз. Начальная скорость движения центра масс маятника при подъеме 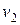, строго говоря, не равна скорости 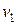перед рывком: 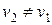. Найти ее можно, зная высоту подъема 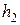и время подъема :

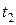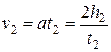. (14)

Расстояние h₂ несколько меньше, чем расстояние h, пройденное при спуске. Потери механической энергии маятника за один цикл движения можно определить по разность этих высот:

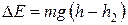. (15)

Причиной этих потерь является работа силы трения о воздух, а также неупругие потери в нити во время рывка. Как уже было сказано выше, кинетическая энергия маятника состоит из двух частей:

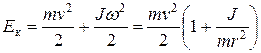. (16)

Радиус диска во много раз превышает радиус стержня, поэтому 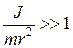, а это значит, что кинетическая энергия вращательного движения во много раз превышает кинетическую энергию поступательного движения.

При ударе теряется малая часть энергии маятника Максвелла 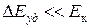, и отношение скоростей после удара и до удара близко к единице. Поэтому в данной системе можно наблюдать многократное повторение цикла движений вниз и вверх, похожие на колебания, а система получила название «маятник».

Рассчитаем среднюю силу рывка или удара в нижней точке движения маятника. Явление удара сопровождается резкими изменениями сил взаимодействия при очень малом времени этих изменений. Эти силы сначала нарастают, а затем убывают. Зависимость их отвремени нам неизвестна, поэтому здесь не будут применены уравнения движения в явном виде.

Среднее значение силы удара определим как отношение приращения импульса к приращению времени:

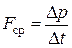. (17)

Поскольку скорость при ударе меняет знак, то изменение импульса равно:

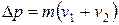. (18)

Потери энергии маятника во время рывка малы, поэтому можно считать, что во время рывка происходит вращение со средней угловой скоростью 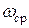, которая равна:

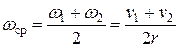. (19)

За время удара будем считать поворота маятника на угол 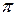со средней угловой скоростью :

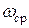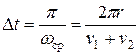. (20)

Тогда средняя сила рывка будет равна:

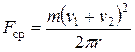. (21)

Более детальный анализ, выполненный в работе [6], показывает, что максимальное значение силы удара 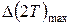превышает найденное среднее значение силы в 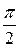раз.

Наблюдая процесс движения маятника, можно убедиться, что отклонение нитей от вертикальной плоскости, возникающее после удара, приводит к появлению небольшого раскачивания оси маятника во время его подъема.