Цель работы: измерение тензора инерции твердого тела и построение его эллипсоида инерции.
Оборудование: установка, секундомер, штангенциркуль.
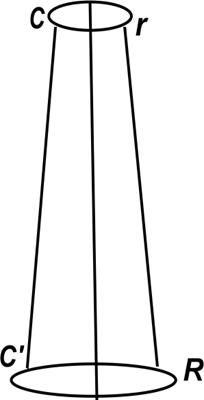 Для измерения моментов инерции твердых тел в работе применяется трифилярный подвес. Платформа радиуса R подвешена на трех нитях длины l к малой платформе радиуса r. Верхняя платформа держится на кронтштейне, прикрепленным к стене, и снабжена рычажком с пружинкой, соединенной с нитью, с помощью которого можно повернуть нижнюю платформу на произвольный угол. При повороте нижней платформы появляется момент упругих сил, стремящийся вернуть платформу в исходное положение, и платформа совершает крутильные колебания.
Для измерения моментов инерции твердых тел в работе применяется трифилярный подвес. Платформа радиуса R подвешена на трех нитях длины l к малой платформе радиуса r. Верхняя платформа держится на кронтштейне, прикрепленным к стене, и снабжена рычажком с пружинкой, соединенной с нитью, с помощью которого можно повернуть нижнюю платформу на произвольный угол. При повороте нижней платформы появляется момент упругих сил, стремящийся вернуть платформу в исходное положение, и платформа совершает крутильные колебания.
Рис. 6. Трифилярный подвес.
Теория эксперимента. Получимвыражение для компонент тензора инерции, для этого рассмотрим твердое тело произвольной формы, закрепленное таким образом, что оно может вращаться вокруг неподвижной точки - центра масс тела. Введем декартову систему координат с началом в центре масс. Твердое тело является системой материальных точек, которыми мы будем считать бесконечно малые объемы, составляющие тело. Каждый i- й объем будет иметь массу 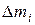 и радиус- вектор
и радиус- вектор 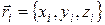 , проведенный из начала координат в точку, где находится i –элемент, а также скорость
, проведенный из начала координат в точку, где находится i –элемент, а также скорость 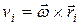 , где
, где 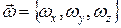 – вектор угловой скорости, описывающий вращение твердого тела. Момент импульса тела относительно центра масс определяется как сумма моментов импульса составляющих его материальных точек:
– вектор угловой скорости, описывающий вращение твердого тела. Момент импульса тела относительно центра масс определяется как сумма моментов импульса составляющих его материальных точек:
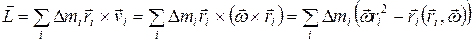 . (1)
. (1)
Распишем формулу (1) по проекциям на координатные оси, получим
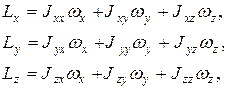 (2)
(2)
где девять величин 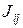 симметричного тензора определяются по формулам:
симметричного тензора определяются по формулам:
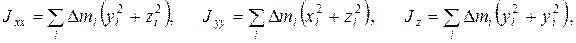
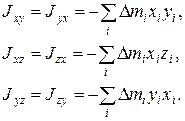 (3)
(3)
Формулу (2) запишем в матричном виде:
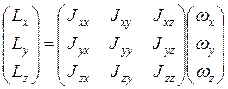 . (4)
. (4)
Или кратко: 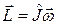 . Величина
. Величина 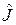 называется тензором инерции твердого тела. Векторы
называется тензором инерции твердого тела. Векторы 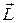 и
и 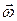 могут быть неколлинеарными.
могут быть неколлинеарными.
Величины 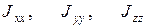 являются диагональными элементами тензора и называются осевыми моментами инерции. Компоненты тензора
являются диагональными элементами тензора и называются осевыми моментами инерции. Компоненты тензора 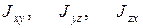 являются недиагональными элементами и носят название его центробежных элементов. Тензор, у которого равны элементы, симметричные относительно главной диагонали называется симметричным тензором. Из формул (3) видно, что тензор инерции является симметричным. В курсе линейной алгебры доказывается, что симметричный тензор может быть приведен к диагональному виду, то есть можно выбрать такую систему координат, чтобы все недиагональные элементы обратились в ноль. Такие направления координатных осей называются главными осями инерции, а величины
являются недиагональными элементами и носят название его центробежных элементов. Тензор, у которого равны элементы, симметричные относительно главной диагонали называется симметричным тензором. Из формул (3) видно, что тензор инерции является симметричным. В курсе линейной алгебры доказывается, что симметричный тензор может быть приведен к диагональному виду, то есть можно выбрать такую систему координат, чтобы все недиагональные элементы обратились в ноль. Такие направления координатных осей называются главными осями инерции, а величины 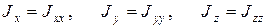 – главными моментами инерции тела.
– главными моментами инерции тела.
Если твердое тело вращается вокруг закрепленной оси, направление которой совпадает с направлением вектора угловой скорости 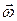 , то удобно представить радиус-вектор
, то удобно представить радиус-вектор 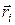 i -го элемента тела, как сумму двух векторов, один из которых параллелен оси вращения, а другой перпендикулярен ей:
i -го элемента тела, как сумму двух векторов, один из которых параллелен оси вращения, а другой перпендикулярен ей:
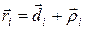 , (5)
, (5)
где 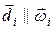 ,
, 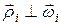 . Скорость i -го элемента равна векторному произведению угловой скорости на его радиус-вектор:
. Скорость i -го элемента равна векторному произведению угловой скорости на его радиус-вектор:
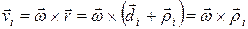 . (6)
. (6)
При рассмотрении этого случая введем понятие момента импульса относительно фиксированной оси. Если ось проходит через центр масс, то соответствующий момент импульса равен:
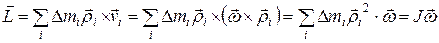 , (7)
, (7)
где
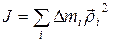 (8)
(8)
является моментом инерции относительно оси, определяющей направление вектора угловой скорости 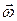 . Введем направляющие косинусы, чтобы выразить момент инерции J через координаты i -го элемента
. Введем направляющие косинусы, чтобы выразить момент инерции J через координаты i -го элемента
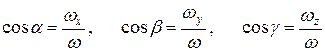 , (9)
, (9)
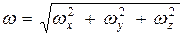 . (10)
. (10)
По теореме Пифагора 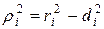 . Рассмотрим отдельно
. Рассмотрим отдельно 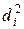
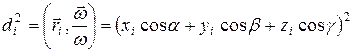 (11)
(11)
Представим J в виде
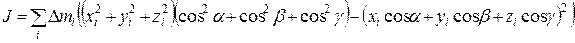 . (12)
. (12)
Перегруппируем в последней формуле члены по степеням косинусов, получим:
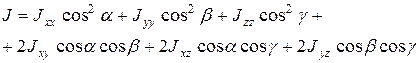 (13)
(13)
В соотношении (13) компоненты тензора инерции определены относительно некоторой неподвижной системы координат, поэтому при вращении тела все они меняют свою величину. В то же время, как видно из определения момента инерции относительно оси (8), он должен оставаться неизменным при вращении тела. Пусть в некоторый момент времени тензор принимает в данной системе координат диагональный вид:
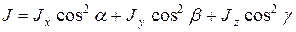 . (14)
. (14)
Поэтому для определения J по формуле (13) возьмем произвольный момент времени, когда система координат, связанная с телом, совпадает с неподвижной системой координат. Таким образом, мы будем рассматривать компоненты 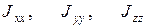 и т. д. в уравнении (13) как определенные в некоторой системе координат, связанной с телом. Рассмотрим геометрическую интерпретацию соотношения (13). В декартовой системе координат для каждого из направляющих косинусов cos α, cos β, cos γ оси вращения отложим по осям OX, OY, OZ величины
и т. д. в уравнении (13) как определенные в некоторой системе координат, связанной с телом. Рассмотрим геометрическую интерпретацию соотношения (13). В декартовой системе координат для каждого из направляющих косинусов cos α, cos β, cos γ оси вращения отложим по осям OX, OY, OZ величины
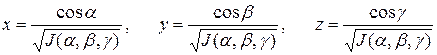 (15)
(15)
Множество точек с координатами (x,y,z) определяет некоторую поверхность. Чтобы найти уравнение этой поверхности, подставим в (13) направляющие косинусы, выраженные через (x,y,z):
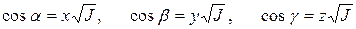 . (16)
. (16)
Получим уравнение поверхности второго порядка
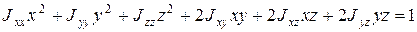 . (17)
. (17)
Поверхность, описываемая данным уравнением, является эллипсоидом. Такой эллипсоид называется эллипсоидом инерции. В главных осях он запишется в более компактном виде:
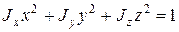 . (18)
. (18)
С помощью этого эллипсоида можно определить значение момента инерции если заданы направляющие косинусы оси. Проведем из центра эллипсоида прямую l с направляющими косинусами 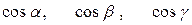 . Расстояние от начала координат до пересечения этой прямой с поверхностью эллипсоида будет равно
. Расстояние от начала координат до пересечения этой прямой с поверхностью эллипсоида будет равно
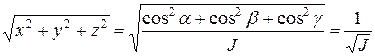 . (19)
. (19)
Для измерения моментов инерции твердого тела в данной работе будет использоваться трифилярный подвес. Круглая платформа подвешена на трех нитях одинаковой длины к платформе меньшего диаметра. Малая платформа укреплена на кронштейне и снабжена рычагом с пружиной, при помощи которых системе можно сообщить крутильные колебания.Если повернуть верхнюю платформу на некоторый угол φ, то увеличится ее потенциальная энергия. Пусть сначала нижняя платформа находится на Z0 ниже верхней, после поворота, она уже будет на высоте Z, так что приращение высоты нижней платформы равно 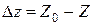 , тогда если пренебречь силами трения согласно закону сохранения энергии получим:
, тогда если пренебречь силами трения согласно закону сохранения энергии получим:
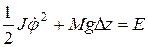 , (20)
, (20)
где J – момент инерции платформы вместе с исследуемым телом, E – полная энергия системы. Приращение потенциальной энергии нижней платформы выразим через угол поворота платформы. Для этого поместим начало координат в центре верхней платформы. Тогда точка С, показанная на рисунке 6, имеет координаты (r, 0, 0), а точка С’ нижней плоскости после поворота на угол φ будет иметь координаты (R cos φ, R sin φ, Z). Расстояние 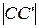 равно длине нити l. То есть квадрат длины
равно длине нити l. То есть квадрат длины 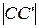 равен квадрату длины нити:
равен квадрату длины нити:
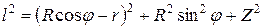 . (21)
. (21)
Первоначальное расстояние между платформами равно Z0, поэтому, согласно теореме Пифагора:
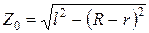 . (22)
. (22)
Из уравнений (21) и (22) следует, что
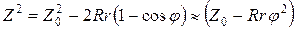 . (23)
. (23)
Здесь было применено приближение для малых углов 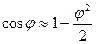 . Тогда при малых углах φ
. Тогда при малых углах φ
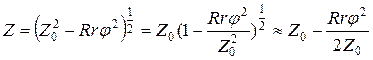 . (24)
. (24)
Очевидно, что 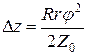 . (25)
. (25)
Подставим это выражение в (20):
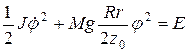 . (26)
. (26)
Продифференцируем (26) по времени и сократим на 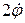 , получим:
, получим:
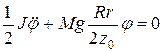 . (21)
. (21)
Решением данного дифференциального уравнения являются функции, вида:
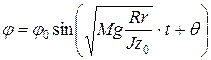 . (22)
. (22)
Амплитуда φ0 и фаза θ определяются начальными условиями. Множитель
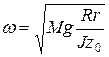 (23)
(23)
является собственной циклической частотой колебаний. Тогда период колебаний:
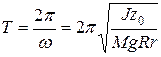 . (24)
. (24)
Зная период колебаний, можно рассчитать момент инерции, как в случае пустой платформы так и платформы с грузом:
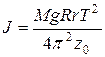 . (25)
. (25)
 2015-05-13
2015-05-13 3281
3281








