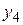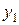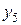2015-05-13
893
Для удобства расчетов и анализа результатов масштабы факторов выбирают так, чтобы значение верхнего уровня соответствовало +1, а нижнего –1. Для этого делают преобразование координат и переходят к ноpмированному масштабу
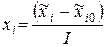, (2.2)
где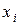 
– нормированное значение; 
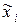– натуральное значение; 
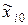– основной уровень; 
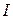– интервал варьирования.
2.2. Составление матрицы планирования полного факторного
эксперимента
Таблица 2.2 МП ПФЭ типа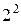 
Таблица 2.3 МП ПФЭ типа
|
В табл. 2.2 для примера приведена матрица планирования для полного факторного эксперимента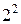 
, которую называют базовой, так как с ее помощью легко построить матрицы любого порядка. Так, для построения матрицы 
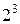, сочетаем базовую матрицу с нижним и верхним уровнями 
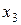(табл. 2.3). Легко заметить, что в первом столбце знаки меняются поочередно, во втором через 2, в третьем – 4, и так далее, что соответствует 
.
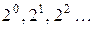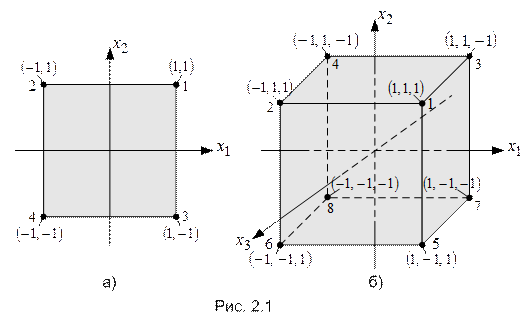
Геометрической интерпретацией ПФЭ 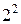является квадрат в факторной плоскости (рис. 2.1,а), ПФЭ 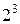– куб (рис. 2.1,б). Здесь нормированные координаты 
, 
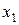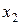и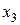 
проходят через точку пересечения основных уровней факторов и масштаб их осей выбран так, чтобы интервал варьирования был равен единице.
Тогда условия проведения опытов соответствуют вершинам. Если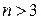 
, то фигуру, задающую в многомерном пространстве область эксперимента, называют
гиперкубом.
Матрицу планирования ПФЭ, включающую взаимодействия различного порядка, обычно называют развернутой. При этом знаки в столбцах для взаимодействий получают перемножением знаков взаимодействующих факторов. Пример развернутойМП эксперимента дан в табл. 2.4. Условный фактор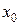 
введен для удобства машинного расчета свободного члена 
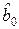. Заметим, что план ПФЭ является центральным и обладает свойством ортогональности, что позволяет после исключения незначимых коэффициентов не пересчитывать оценки оставшихся коэффициентов и их дисперсии.
Кроме того, план ПФЭ для линейных ММ обладает также свойством рототабельности и является A-,D- и G-оптимальным. Для матрицы, содержащей взаимодействия, свойство рототабельности не выполняется.
Таблица 2.4
Развернутая МП для ПФЭ типа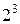
 | | | | |  |  |  |  |  |
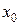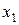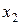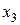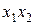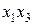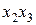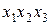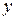| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |  | |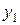
| +1 | –1 | +1 | +1 | –1 | –1 | +1 | –1 |  | |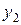
| +1 | +1 | –1 | +1 | –1 | +1 | –1 | –1 |  | |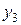
| +1 | –1 | –1 | +1 | +1 | –1 | –1 | +1 |  | |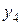
| +1 | +1 | +1 | –1 | +1 | –1 | –1 | –1 |  | |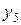
| +1 | –1 | +1 | –1 | –1 | +1 | –1 | +1 |  | |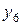
| +1 | +1 | –1 | –1 | –1 | –1 | +1 | +1 |  | |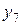
| +1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 |  |
