2015-05-13
338
Как уже отмечалось выше, гипотеза о статистической значимости (отличии от нуля) коэффициентов регрессии проверяется критерием Стьюдента. Расчетное значение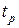 
этого критерия определяют как частное от деления модуля оценки коэффициента 
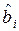на оценку его среднеквадратического отклонения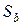 
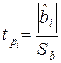. (2.4)
В ПФЭ благодаря одинаковой удаленности всех экспериментальных точек факторного пространства от центра эксперимента, оценки всех коэффициентов уравнения регрессии независимо от их величины вычисляются с одинаковой погрешностью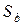 
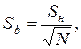
где
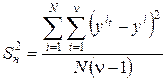(2.5)
является оценкой дисперсии единичного наблюдения.
Оценку дисперсии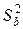 
коэффициентов можно найти и с помощью дисперсионной матрицы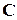 
,
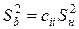где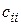 
– элементы главной диагонали дисперсионной матрицы 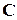, которые при ПФЭ все одинаковы и равны 
.
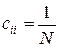Критическое значение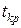 
критерия находят из таблицы распределения Стьюдента по числу степеней свободы 
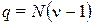и уровню значимости 
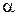(прил. 5). Если 
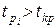, гипотеза о значимости коэффициента 
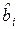принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.
Необходимо помнить, что незначимость коэффициента может быть обусловлена неверным выбором интервала варьирования фактора. Поэтому иногда бывает полезным изменить интервал варьирования и провести новый эксперимент.
