Пусть требуется исследовать влияние производственных факторов (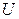 – опорное напряжение
– опорное напряжение 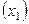 ,
, 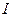 – ток потребления
– ток потребления 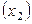 ,
, 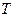 – конечная температура нагрева
– конечная температура нагрева 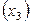 ) на качество производства магнитных дисков. Номинальные значения факторов:
) на качество производства магнитных дисков. Номинальные значения факторов: 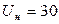 В,
В,
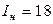 А,
А, 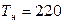
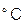 .
.
В этом случае ПФЭ дает возможность построить полиномиальную ММ следующего вида:
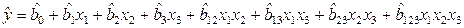 .
.
Поставим ПФЭ при трех сериях опытов в точках: 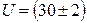 В,
В, 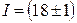 A,
A, 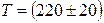
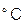 . Условия проведения опытов сведем в табл. 2.5. и проведем нормирование масштабов факторов.
. Условия проведения опытов сведем в табл. 2.5. и проведем нормирование масштабов факторов.
Таблица 2.5
Условия проведения ПФЭ
| Характеристика плана | 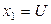 , B , B | 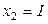 , А , А | 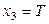 , , 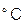 |
| Нулевой уровень | |||
| Интервал варьирования | |||
| Верхний уровень | |||
| Нижний уровень |
Cоставим МП эксперимента, в соответствии с которой проведем рандомизированные опыты. Полученные результаты запишем в табл. 2.6, где 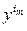 – численные значения исследуемого параметра,
– численные значения исследуемого параметра, 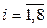 – номер точки в факторном пространстве,
– номер точки в факторном пространстве, 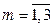 – номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
– номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
Проведем статистическую обработку полученных результатов. Для проверки по критерию Кохрена воспроизводимости опытов при выбранном уровне значимости 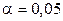 вычислим в каждой точке факторного пространства (их у нас
вычислим в каждой точке факторного пространства (их у нас 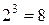 ) среднее значение
) среднее значение
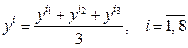
и оценки дисперсий
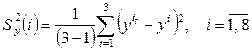 .
.
Критическое значение 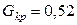 найдем из таблицы G-распределения (прил. 4) при
найдем из таблицы G-распределения (прил. 4) при 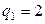 ,
, 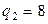 . С помощью соотношения (2.3) найдем
. С помощью соотношения (2.3) найдем 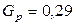 . Поскольку
. Поскольку 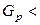
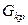 считаем, что дисперсии наблюдений во всех точках факторного пространства однородны.
считаем, что дисперсии наблюдений во всех точках факторного пространства однородны.
Расчет оценок коэффициентов регрессионного уравнения 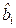 проведем двумя способами.
проведем двумя способами.
1.Алгебраическим: 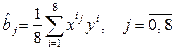 .
.
2.Матричным. Для этого составим матрицу планирования эксперимента

и найдем дисперсионную матрицу 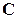
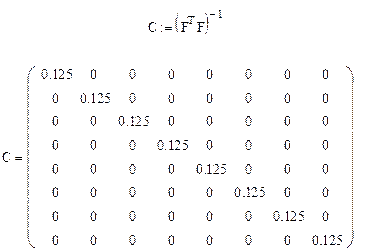
Вычислим оценки коэффициентов 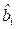
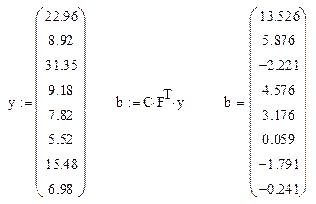
Сравнивая результаты, видим, что оценки, полученные обоими способами, совпадают.
По критерию Стьюдента (соотношение (2.4)) определим статистическую значимость коэффициентов регрессии при уровне значимости 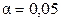 , для которого при
, для которого при 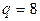 критическое значение
критическое значение 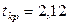 . При этом, как видно из матрицы
. При этом, как видно из матрицы 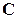 , оценки дисперсий всех
, оценки дисперсий всех 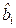 вычисляются по формуле
вычисляются по формуле
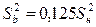 ,
,
где 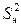 – оценка дисперсии единичного наблюдения, вычисленная по соотношению (2.5).
– оценка дисперсии единичного наблюдения, вычисленная по соотношению (2.5).
В нашем случае 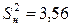 , следовательно,
, следовательно, 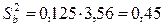 . Поэтому
. Поэтому 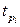 вычисляются как
вычисляются как 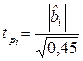 . Результаты занесем в табл. 2.6. Исключим из ММ незначимые коэффициенты регрессии
. Результаты занесем в табл. 2.6. Исключим из ММ незначимые коэффициенты регрессии 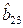 и
и 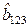 . При этом благодаря ортогональности плана оценки остальных коэффициентов не изменятся.
. При этом благодаря ортогональности плана оценки остальных коэффициентов не изменятся.
По критерию Фишера (1.5) проверим адекватность линейной ММ при 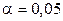 .
.
Для этого нужны оценки дисперсий единичного наблюдения и неадекватности. Дисперсия единичного наблюдения уже найдена и равна 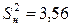 . Найдем оценку дисперсии неадекватности
. Найдем оценку дисперсии неадекватности
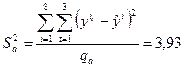 ,
,
где 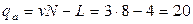 .
.
Найдем 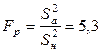 и
и 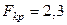 (используя таблицу F-распределения (прил. 6) и число степеней свободы числителя
(используя таблицу F-распределения (прил. 6) и число степеней свободы числителя 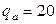 и знаменателя
и знаменателя 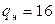 ). Так как
). Так как 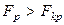 , то линейная модель неадекватна. В этом случае необходимо добавить эффект взаимодействия с наибольшим по модулю коэффициентом, в нашем случае это
, то линейная модель неадекватна. В этом случае необходимо добавить эффект взаимодействия с наибольшим по модулю коэффициентом, в нашем случае это 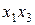 . Теперь
. Теперь 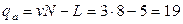 ,
, 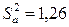 . При этом
. При этом 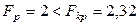 , то есть модель адекватна. Делаем вывод о том, что полученная ММ с уровнем значимости
, то есть модель адекватна. Делаем вывод о том, что полученная ММ с уровнем значимости 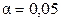 не противоречит экспериментальным результатам.
не противоречит экспериментальным результатам.
Переходим к натуральному масштабу:
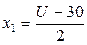 ,
, 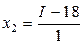 ,
, 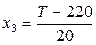 ,
,
где 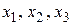 – нормированные значения,
– нормированные значения, 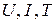 – значения в натуральном масштабе.
– значения в натуральном масштабе.
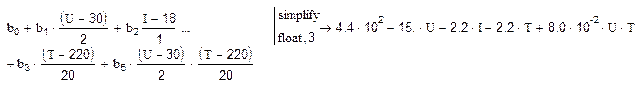
Таким образом, окончательно получаем ММ:
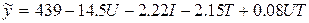 .
.
 2015-05-13
2015-05-13 2054
2054








