2015-05-13
1262
В полой трубе с прямоугольным поперечным сечением и с идеально проводящими стенками возбуждено монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, относительная диэлектрическая проницаемость которой равна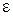 
. Относительная магнитная проницаемость среды 
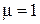. Заданы поперечные размеры волновода, индексы 
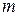и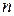 
типов волн, частота монохроматической волны 
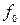, амплитуды электрической 
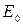или магнитной 
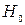составляющих электромагнитного поля (таблица В.1 приложения В).
Задание:
1 Определить основные параметры электромагнитного поля
2 Рассчитать комплексные амплитуды всех составляющих векторов поля.
3 Определить диапазон частот, в котором рассматриваемое поле - бегущая волна.
4 Записать выражение для мгновенных значений всех составляющих векторов поля для случая, когда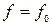 
.
5 Рассчитать и построить графики зависимостей мгновенных значений всех составляющих полей от продольной координаты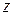 
(при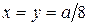 
) в два момента времен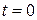и 
и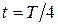 
в интервале 
.
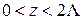6 Проверить выполнение граничных условий на боковых стенках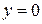 
, 
, 
, 
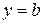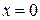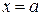трубы с прямоугольным поперечным сечением для касательной составляющей вектора 
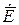и нормальной составляющей вектора 
.
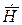7 Определить максимальные значения плотности продольного поверхностного тока на стенках волновода.
8 Вычислить средний за период поток энергии через поперечное сечение волновода.
9 Определить фазовую скорость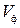 
и скорость распространения энергии волны 
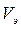, построить графики зависимосте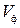й и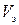 
от частоты.
10 Построить структуру векторных линий полей и токов на стенках волновода.
