Значения M(x) и D(x) характерны для бесконечной последовательности чисел. Поэтому оценки математического ожидания 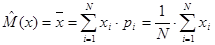 и дисперсии
и дисперсии 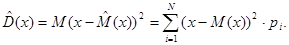 , полученные на основе конечной последовательности чисел, будут отличаться от теоретических. По величине модуля разности
, полученные на основе конечной последовательности чисел, будут отличаться от теоретических. По величине модуля разности 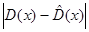 и
и 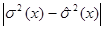 можно судить о принадлежности выборки к совокупности чисел с равномерным законом распределения.
можно судить о принадлежности выборки к совокупности чисел с равномерным законом распределения.
Вычисляем оценки параметров распределения либо их точечные оценки:
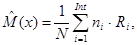
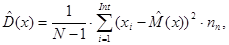 где величина
где величина 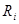 - середина
- середина 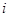 -го интервала разбиения области реализации значений величины Х.
-го интервала разбиения области реализации значений величины Х.
Контрольные вопросы.
1. Определение случайной величины и ее характеристик.
2. Равномерный закон распределения случайной величины.
3. Алгоритмы получения выборок ПСЧ, используемые в данной работе.
4. Алгоритм построения гистограммы функции плотности вероятности.
5. Нахождение оценок параметров случайной выборки.
6. Сущность проверки по критерию согласия 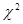 .
.
 2015-05-13
2015-05-13 344
344








