2015-05-13
419
Интервал апериодичности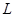 
- интервал, на котором отсутствует повторение r чисел, то есть событие 
.
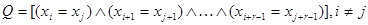Например,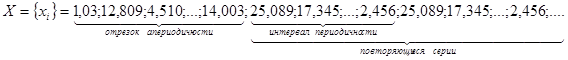 
Практика показывает, что с увеличением r интервал апериодичности возрастает. При больших значениях r для экспериментального определения L может потребоваться длительное время. Поэтому она ограничивается проверкой выборки объемом n ПСЧ, определяемым дополнительно для конкретной задачи.
Если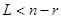 
, то в последовательности для некоторых i и j событие Q имеет место. Минимальная разность j-i, для которой выполняется условие (…), равно периоду последовательности T. Суммируя наименьшее i, при котором выполняется условие 
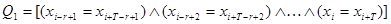, с периодом последовательности T, получаем искомое значение интервала апериодичности: 
.
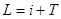Если событие Q 1 не происходит, то констатируется факт, что L > n.
