Проверка случайности методом серий

Для проверки случайности преобразуем получаемые при помощи ГПСЧ числа следующим образом:

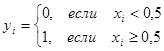
В полученной последовательности 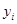выявляем серии. Серией называется отрезок выборки, состоящий из идущих подряд элементов одного типа. Число элементов серии называется ее длиной. Тип серии характеризуется значением элементов выборки .

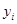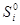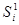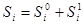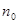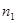Обозначим через и соответственно число серий типа 0 и 1 длиной i; - общее число серий длины i; S – общее число серий в выборке, и - соответственно число элементов в выборке объемом .

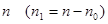При случайном чередовании элементов выборки вероятность появления общего числа серий определяется по формуле:

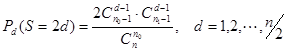для четного числа серий и

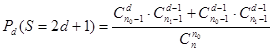для нечетного числа серий.

Выявляя вероятность при разных 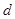, можно построить теоретический закон распределения общего числа серий при известном объеме выборки. При увеличении объема выборки закон распределения общего числа серий асимптотически приближается к нормальному с характеристиками .

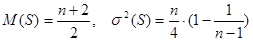Вероятность появления общего числа серий вычисляется по формуле (*),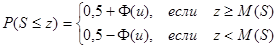

где 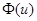нормированный закон нормального распределения. Формулой (*) можно воспользоваться при n >20. Задаваясь вероятностью a отклонения верной гипотезы по таблице нормированного нормального закона распределения (см. приложение) находят u_a и из формулы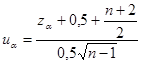

получают минимально допустимое значение общего числа серий S_min=z_a, учитывая, что u_a при 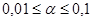- величина отрицательная. Если в используемой выборке общее число серий окажется больше S_min, то гипотеза о случайности принимается. Рассмотренная проверка называется проверкой по количеству серий.

Можно сделать проверку и по максимальной длине серий. Для этого случая доказано, что для серий большой длины закон распределения 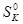и 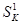( 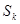- число серий не менее К) при 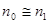хорошо аппроксимируется законом распределения Пуассона 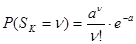(*), где .

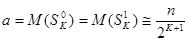На основании (*) получим вероятность появления хотя бы одной серии длиной не меньше К . (**)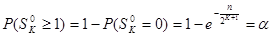

Задаваясь a, из (**) находят критическое значение длины серии 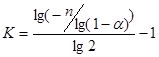. Если исследуемая выборка не содержит серий длиннее K при заданном уровне значимости a, то гипотеза о случайности принимается.