Требуется построить гистограммы интегральной функции распределения и функции плотности вероятности (дифференциальной функции распределения).
Последовательность построения гистограмм:
1) Построение вариационного ряда.
Полученную выборку псевдослучайных чисел 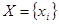 располагаем в порядке возрастания значения
располагаем в порядке возрастания значения 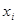 , находим
, находим 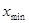 и
и 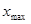 .
.
2) Определяем область реализации R (вариационный размах) полученной случайной выборки 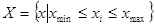 :
: 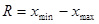 .
.
3) Вычисляем количество интервалов разбиения
Предварительное количество интервалов, на которое должен быть разбит интервал 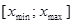 , можно найти при помощи оценочных формул:
, можно найти при помощи оценочных формул:
- число интервалов 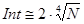 , это примерно
, это примерно 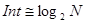 . Величина интервала разбиения
. Величина интервала разбиения 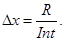
С другой стороны, можно воспользоваться формулой Стерджесса для нахождения длины интервалов разбиения: 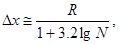 (величина Dx подбирается таким образом, чтобы количество интервалов Int было целым числом) и вычислить число интервалов разбиения
(величина Dx подбирается таким образом, чтобы количество интервалов Int было целым числом) и вычислить число интервалов разбиения 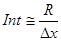 .
.
4) Определяют число попаданий реализации псевдослучайной величины Х в заданные интервалы 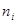 , вычисляем относительные частоты
, вычисляем относительные частоты 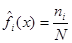 ,
, 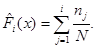
5) Строим гистограммы функции плотности вероятности распределения и интегральной функции вероятности. Диаграмма накопленных частот является аналогом интегрального закона распределения.
Принадлежность полученной выборки равномерному закону распределения можно проверить с помощью теста частот.
Тест частот:
Замечание: Объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждая группа должна содержать не менее 5-8 вариантов; малочисленные группы следует объединять в одну, суммируя частоты.
Интервал реализации случайной величина разбивается на 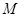 равно протяженных интервалов (обычно
равно протяженных интервалов (обычно 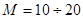 ). Полученные эмпирические частоты
). Полученные эмпирические частоты 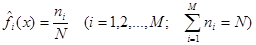 сравниваются с теоретическими вероятностями
сравниваются с теоретическими вероятностями 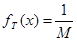 . Согласие проверяется по критерию «хи-квадрат». Эмпирическое (опытное) значение величины хи-квадрат вычисляется по следующей формуле:
. Согласие проверяется по критерию «хи-квадрат». Эмпирическое (опытное) значение величины хи-квадрат вычисляется по следующей формуле: 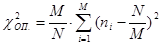 . Оно сравнивается с теоретическим значением величины хи-квадрат, которое находится как критическая точка распределения хи-квадрат с заданными уровнем значимости
. Оно сравнивается с теоретическим значением величины хи-квадрат, которое находится как критическая точка распределения хи-квадрат с заданными уровнем значимости 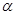 и числом степеней свободы
и числом степеней свободы 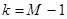 :
: 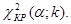
Если 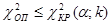 - принимается гипотеза о принадлежности исследуемой выборки равномерному закону распределения.
- принимается гипотеза о принадлежности исследуемой выборки равномерному закону распределения.
Если 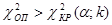 - гипотеза о принадлежности исследуемой выборки равномерному закону распределения отвергается.
- гипотеза о принадлежности исследуемой выборки равномерному закону распределения отвергается.
Критерий Колмогорова применяют при наличии данных об интегральном законе распределения. В качестве функционала используют максимальную разность между теоретическим 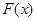 и эмпирическим
и эмпирическим 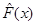 законами распределения
законами распределения 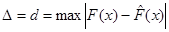 .
.
Колмогоров показал, что 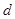 умножение на n – случайная величина, которая имеет функцию распределения
умножение на n – случайная величина, которая имеет функцию распределения 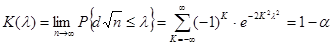 .
.
Значение 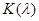 (см. приложение 2) дает вероятность того, что величина
(см. приложение 2) дает вероятность того, что величина 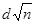 не будет превосходить параметр
не будет превосходить параметр 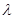 для любой теоретической функции
для любой теоретической функции 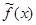 .
.
 2015-05-13
2015-05-13 891
891








