Мы рассмотрим только одну из многих разновидностей матричных игр, а именно, антагонистическую игру двух лиц с нулевой суммой. Постановка задачи такова. В игре участвуют два игрока, в распоряжении которых имеется конечный набор решений, называемых стратегиями. Пусть у первого игрока имеется 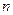 стратегий
стратегий 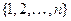 , а у второго
, а у второго 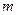 стратегий
стратегий 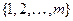 . Игроки равноправны в том смысле, что они принимают решение одновременно и не знают о решении своего противника. Если первый игрок принял решение номер
. Игроки равноправны в том смысле, что они принимают решение одновременно и не знают о решении своего противника. Если первый игрок принял решение номер 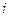 , а второй игрок принял решение номер
, а второй игрок принял решение номер 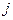 , то второй игрок должен выплатить первому платеж
, то второй игрок должен выплатить первому платеж 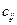 (при этом величина
(при этом величина 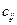 может быть и отрицательной). Матрица
может быть и отрицательной). Матрица
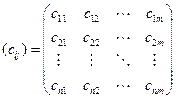
называется платежной. Естественно, первый игрок (получатель платежа) желает принять такое решение, которое бы увеличило платеж, а второй хотел бы принять такое решение, которое бы уменьшило величину платежа. Вопрос заключается в следующем - как действовать каждому из игроков в этой ситуации, с учетом их противоположных интересов?
Определение. Назовем верхней ценой 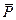 игры минимальный платеж, который может гарантировать второй игрок при условии, что он должен заранее сообщить о своей стратегии первому игроку.
игры минимальный платеж, который может гарантировать второй игрок при условии, что он должен заранее сообщить о своей стратегии первому игроку.
Определим верхнюю цену игры. Если второй игрок сообщает первому, что он выбрал первую стратегию (первый столбец платежной матрицы), то первый игрок выберет такую стратегию (строку платежной матрицы), в которой стоит максимальное в первом столбце число, то есть выберет максимум из чисел
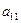 ,
, 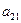 ,
, 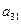 , ¼,
, ¼, 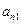 .
.
Для второй, третьей, четвертой и так далее стратегий второго игрока ситуация аналогична: первый игрок выберет ту стратегию, которая гарантирует ему получения максимума из чисел
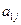 ,
, 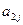 ,
, 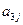 , ¼,
, ¼, 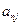 .
.
Как, очевидно, следует в этой ситуации поступить дискриминированному второму игроку? ¾ естественно, выбрать наименьшее число из соответствующих максимумов и сыграть ту стратегию, где это минимум достигается. Следовательно,
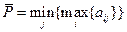 .
.
Номер стратегии 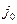 , которая гарантирует наименьший возможный проигрыш второму игроку в ситуации, когда он дискриминирован, называется минимаксной стратегией второго игрока.
, которая гарантирует наименьший возможный проигрыш второму игроку в ситуации, когда он дискриминирован, называется минимаксной стратегией второго игрока.
Определение. Назовем нижней ценой 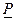 игры максимальный платеж, который может гарантировать первый игрок при условии, что он заранее сообщает о выбранной стратегии второму игроку.
игры максимальный платеж, который может гарантировать первый игрок при условии, что он заранее сообщает о выбранной стратегии второму игроку.
Определим нижнюю цену игры. Ясно, что для этого надо сначала найти минимумы элементов платежной матрицы в каждой строке, а затем выбрать наибольшее число из этих минимумов. Таким образом,
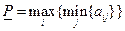 .
.
Стратегия 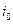 , которая обеспечивает этот наибольший платеж первому игроку в наихудшей для него ситуации, называется максиминной стратегией первого игрока. Из определения следует, что
, которая обеспечивает этот наибольший платеж первому игроку в наихудшей для него ситуации, называется максиминной стратегией первого игрока. Из определения следует, что
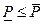 .
.
Если 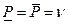 , то
, то 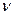 называется ценой игры, а минимаксная и максиминная стратегии являются в некотором смысле наиболее разумным поведением для второго и первого игрока соответственно. Действительно, если один из игроков, например, первый, выбрал максиминную стратегию, то он гарантированно получит платеж, не меньший
называется ценой игры, а минимаксная и максиминная стратегии являются в некотором смысле наиболее разумным поведением для второго и первого игрока соответственно. Действительно, если один из игроков, например, первый, выбрал максиминную стратегию, то он гарантированно получит платеж, не меньший 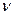 , что бы ни делал второй игрок. При этом уклонение второго игрока от минимаксной стратегии может лишь увеличить плату по сравнению с
, что бы ни делал второй игрок. При этом уклонение второго игрока от минимаксной стратегии может лишь увеличить плату по сравнению с 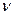 . Аналогично, если второй игрок играет минимаксную стратегию, то больше, чем
. Аналогично, если второй игрок играет минимаксную стратегию, то больше, чем 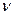 , он не заплатит, в то время как первый игрок получит меньшую плату, чем
, он не заплатит, в то время как первый игрок получит меньшую плату, чем 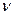 , если он уклонится от максиминной стратегии. Таким образом, в случае существования цены игры, мы нашли разумное поведение для каждого из игроков: они должны выбирать свои максиминную и минимаксную стратегии, при этом платеж будет равен цене игры.
, если он уклонится от максиминной стратегии. Таким образом, в случае существования цены игры, мы нашли разумное поведение для каждого из игроков: они должны выбирать свои максиминную и минимаксную стратегии, при этом платеж будет равен цене игры.
Пример. Рассмотрим игру с платежной матрицей
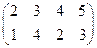 .
.
Найдем верхнюю цену игры. Для этого в каждом столбце подчеркнем наибольший элемент, а затем выберем из них самое маленькое число. Получаем:
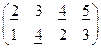 .
.
Следовательно, 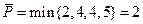 и минимаксная стратегия второго игрока
и минимаксная стратегия второго игрока 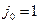 .
.
Найдем нижнюю цену игры. Для этого в каждой строке подчеркнем наименьший элемент, а затем выберем из них самое большое число. Получаем:
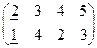 .
.
Следовательно, 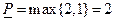 и максиминная стратегия первого игрока
и максиминная стратегия первого игрока 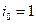 . Поскольку верхняя и нижняя цена игры совпадают, то оптимальным поведением каждого из игроков будет выбор первой стратегии.
. Поскольку верхняя и нижняя цена игры совпадают, то оптимальным поведением каждого из игроков будет выбор первой стратегии.
Что делать игрокам в ситуации, когда цены игры нет? Одним из возможных ответов на этот вопрос является использование так называемых смешанных стратегий игроков.
Определение. Смешанной стратегией игрока называется распределение вероятностей на множестве его стратегий.
Иными словами, смешанной стратегией первого игрока является произвольная случайная величина, принимающая значения 1, 2, 3, ¼, 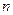 с вероятностями
с вероятностями 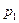 ,
, 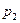 ,
, 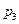 , ¼,
, ¼, 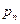 ,
, 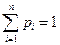 ,
, 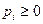 . Аналогично, смешанная стратегия второго игрока есть произвольная случайная величина, принимающая значения принимающая значения 1, 2, 3, ¼,
. Аналогично, смешанная стратегия второго игрока есть произвольная случайная величина, принимающая значения принимающая значения 1, 2, 3, ¼, 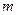 с вероятностями
с вероятностями 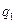 ,
, 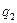 ,
, 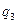 , ¼,
, ¼, 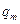 ,
, 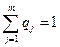 ,
, 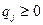 .
.
Таким образом, если, скажем, первый игрок решил играть некоторую смешанную стратегию, то в большой партии из 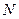 игр он должен так чередовать свои стратегии, что в среднем в
игр он должен так чередовать свои стратегии, что в среднем в 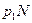 играх он принимал бы первое решение, в
играх он принимал бы первое решение, в 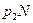 играх он принимал бы второе решение, в
играх он принимал бы второе решение, в 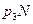 играх он принимал бы третье решение, и так далее.
играх он принимал бы третье решение, и так далее.
При использовании игроками смешанных стратегий плата становится случайной величиной, которая принимает значение 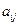 с вероятностью
с вероятностью 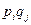 (предполагается, что смешанные стратегии игроков являются независимыми случайными величинами). Среднее значение платы (ее математическое ожидание) равно
(предполагается, что смешанные стратегии игроков являются независимыми случайными величинами). Среднее значение платы (ее математическое ожидание) равно
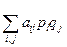 .
.
Первый игрок хотел бы выбрать стратегию 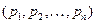 , обеспечивающий максимальный средний выигрыш, а второй игрок за счет выбора стратегии
, обеспечивающий максимальный средний выигрыш, а второй игрок за счет выбора стратегии 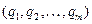 хотел бы минимизировать эту величину.
хотел бы минимизировать эту величину.
Частным случаем смешанной стратегии первого игрока является стратегия, в которой 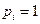 для некоторого номера
для некоторого номера 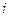 , а
, а 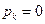 для
для 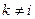 . Такая стратегия называется чистой стратегией. Аналогично определяются чистые стратегии второго игрока.
. Такая стратегия называется чистой стратегией. Аналогично определяются чистые стратегии второго игрока.
Как и при использовании чистых стратегий, при использовании игроками смешанных стратегий мы также можем определить верхнюю и нижнюю цены игры:
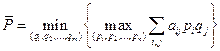 ,
,
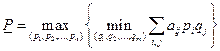 .
.
Теорема о минимаксе утверждает, что для смешанных стратегий для любой платежной матрицы имеет место равенство
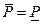 .
.
Следовательно, решением игры является нахождение максиминной и минимаксной смешанных стратегий игроков и определение цены игры.
Нахождение минимаксной и максиминной стратегий основано на следующем факте: если какой-либо игрок привилегирован (то есть до момента принятия решения он уже знает смешанную стратегию противника), то он может использовать свою чистую стратегию (то есть использование смешанной стратегии привилегированным игроком не улучшает для него значение платы 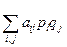 ).
).
Следовательно,
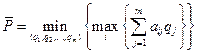 ,
,
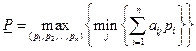 .
.
Имеется два важных следствия из этого утверждения. Первое следствие относится к случаю, когда у одного из игроков имеется всего две стратегии, и позволяет найти оптимальные смешанные стратегии графически. Второе следствие заключается в возможности свести игровую задачу к задаче линейного программирования.
Графический способ решения игры 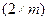 и
и 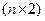 .
.
Рассмотрим сначала случай 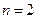 . Тогда у первого игрока имеется всего две стратегии, и его смешанная стратегия имеет вид
. Тогда у первого игрока имеется всего две стратегии, и его смешанная стратегия имеет вид 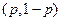 ,
, 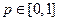 . В этой ситуации для нижней цены игры имеем соотношение
. В этой ситуации для нижней цены игры имеем соотношение
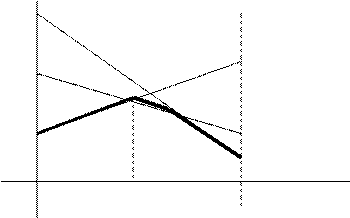
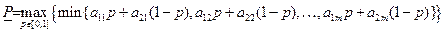 Построив графики функций
Построив графики функций 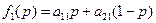 ,
, 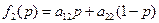 , ¼,
, ¼, 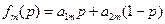 , следует для каждого
, следует для каждого 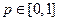 найти наименьшее из значений
найти наименьшее из значений 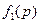 ,
, 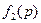 , ¼,
, ¼, 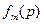 . Обозначим это наименьшее значение
. Обозначим это наименьшее значение 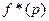 . После этого следует найти такое
. После этого следует найти такое 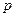 , при котором
, при котором 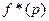 максимально.
максимально.
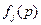
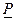
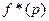
0 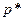 1
1 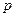
Чтобы найти смешанную стратегию второго игрока, следует определить значения индексов 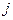 , для которых достигается максимин, то есть
, для которых достигается максимин, то есть 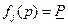 . Пусть это индексы
. Пусть это индексы 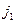 ,
, 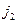 , ¼,
, ¼, 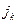 (обычно
(обычно 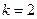 ). После этого остается решить систему
). После этого остается решить систему
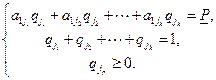
Аналогично, если 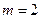 , то смешанные стратегии второго игрока имеют вид
, то смешанные стратегии второго игрока имеют вид 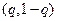 ,и верхняя цена игры определяется из соотношения
,и верхняя цена игры определяется из соотношения
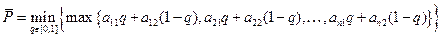 Нам нужно построить графики функций
Нам нужно построить графики функций
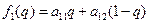 ,
, 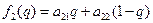 ,¼,
,¼, 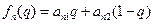
на отрезке 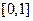 ; определить
; определить
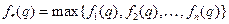
для каждого 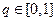 ; после чего найти
; после чего найти 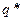 , для которого
, для которого
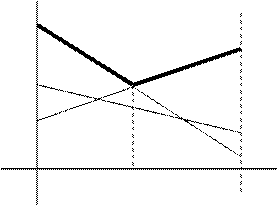
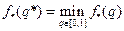 .
.
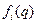
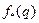
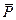
0 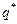 1
1
 2015-05-13
2015-05-13 1558
1558








