Пусть 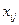 – некоторый допустимый план поставок. Назовем системой потенциалов плана
– некоторый допустимый план поставок. Назовем системой потенциалов плана 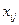 такой набор чисел
такой набор чисел 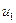 ,
, 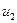 ,…,
,…, 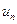 и
и 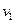 ,
, 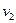 ,…,
,…, 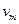 , что выполнены соотношения
, что выполнены соотношения
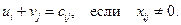
Критерий оптимальности: план 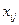 имеет наименьшую стоимость, если существует такая система потенциалов, что для всех индексов
имеет наименьшую стоимость, если существует такая система потенциалов, что для всех индексов 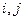 , для которых
, для которых 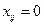 , выполнено соотношение
, выполнено соотношение
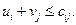
Как определить систему потенциалов? План назовем невырожденным, если число занятых клеток (для которых 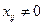 ) равно
) равно 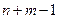 . В этом случае полагаем
. В этом случае полагаем 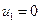 и получаем систему из
и получаем систему из 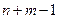 уравнения
уравнения
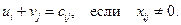
для определения 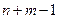 неизвестного. Можно показать, что система имеет единственное решение.
неизвестного. Можно показать, что система имеет единственное решение.
Если число занятых клеток окажется меньше 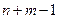 , дополним план до невырожденного, назначив фиктивную, нулевую, поставку в необходимое количество пустых клеток (с наименьшей стоимостью).
, дополним план до невырожденного, назначив фиктивную, нулевую, поставку в необходимое количество пустых клеток (с наименьшей стоимостью).
Пример. Пусть имеется три поставщика с ресурсами 1000, 1500, 1200 и два потребителя с потребностями 2300, 1400. Стоимость поставки единицы груза от 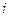 -го поставщика к
-го поставщика к 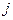 -му потребителю задана транспортной таблицей:
-му потребителю задана транспортной таблицей:
Поскольку 1000+1500+1200=2300+1400, задача закрытая. Определим первоначальное допустимое распределение груза методом северо-западного угла.
Число занятых клеток равно 4=3+2-1, план невырожденный. Уравнения для потенциалов:
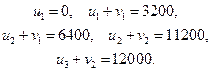
Отсюда 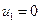 ,
, 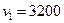 ,
, 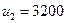 ,
, 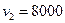 ,
, 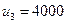 .
.
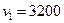 | 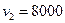 | |
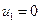 | ||
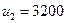 | ||
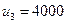 |
Выражения 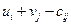 для незанятых клеток пишем в левом нижнем углу. Поскольку
для незанятых клеток пишем в левом нижнем углу. Поскольку 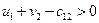 , план поставок неоптимальный.
, план поставок неоптимальный.
Улучшение опорного плана.
Если для первоначального плана не выполнен критерий оптимальности, план можно улучшить, перераспределив поставки по следующему правилу.
Выберем свободную клетку с максимальным значением 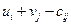 . Пусть это клетка с индексом
. Пусть это клетка с индексом 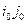 . Соединим ее замкнутой ломаной с занятыми клетками, так чтобы вершины ломаной находились в занятых клетках, а стороны были параллельны сторонам таблицы. Можно показать, что для любого невырожденного плана поставок такая ломаная определена единственным образом.
. Соединим ее замкнутой ломаной с занятыми клетками, так чтобы вершины ломаной находились в занятых клетках, а стороны были параллельны сторонам таблицы. Можно показать, что для любого невырожденного плана поставок такая ломаная определена единственным образом.
Припишем знаки + или - вершинам этой ломаной по следующему правилу: вершине с индексом 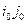 знак +, а любым двум соседним вершинам разные знаки. Найдем минимальную поставку среди вершин со знаком -. Теперь именно это количество груза убавим у вершин со знаком - и прибавим к вершинам со знаком +. Перераспределение поставок закончено.
знак +, а любым двум соседним вершинам разные знаки. Найдем минимальную поставку среди вершин со знаком -. Теперь именно это количество груза убавим у вершин со знаком - и прибавим к вершинам со знаком +. Перераспределение поставок закончено.
  1000- 1000- |  7200 + 7200 + | ||
 1300 + 1300 + | - 200 | ||
В результате получаем
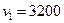 | 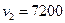 | ||
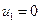 | |||
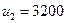 | -800 | ||
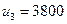 | -200 | ||
План оптимальный.
Задача 6.3. В городе имеется три хлебозавода, которые выпускают одинаковую продукцию и развозят ее по 5 магазинам. Стоимость доставки пропорциональна расстоянию от завода до магазина (см. таблицу).
| Завод | Расстояние до магазина (км) | ||||
| №1 | №2 | №3 | №4 | №5 | |
| I | |||||
| II | |||||
| III |
Мощности хлебозаводов составляют 40, 100 и 140 тонн продукции в сутки. Суточные потребности магазинов равны соответственно 20, 50, 60, 40, 110 тонн. Определите план поставок, минимизирующий суммарные транспортные расходы магазинов.
Решение. Запишем данные задачи в виде транспортной таблицы.
Определим первоначальное распределение поставок методом северо-западного угла.
Число занятых клеток равно 7, при этом 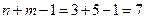 , то есть план невырожденный. Рассчитаем систему потенциалов.
, то есть план невырожденный. Рассчитаем систему потенциалов.
Полагаем 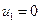 . В первой строке две занятые клетки, поэтому
. В первой строке две занятые клетки, поэтому
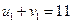 ,
, 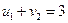 ,
,
откуда
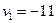 ,
, 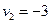 .
.
В первом столбце других занятых клеток нет. Во втором столбце имеется поставка во второй строке, поэтому
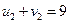 Û
Û 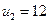 .
.
Теперь мы знаем потенциал второй строки и можем найти потенциалы третьего и четвертого столбца.
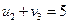 ,
, 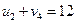 .
.
Получаем:
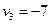 ,
, 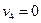 .
.
В четвертом столбце занята поставкой клетка третьей строки, поэтому
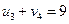 Û
Û 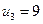 .
.
Остается найти потенциал последнего, пятого, столбца.
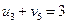 Û
Û 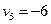 .
.
Запишем полученные результаты в виде таблицы.
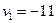 | 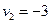 | 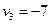 | 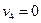 | 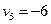 | |
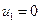 | |||||
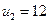 | |||||
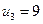 |
Найдем величины 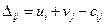 для всех незанятых поставками клеток.
для всех незанятых поставками клеток.
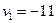 | 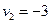 | 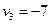 | 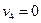 | 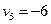 | |
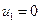 | -1 | -10 | -11 | ||
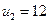 | -9 |   30 30 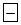 |   10 10 | -3 | |
 | -10 | 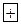  | -5 | 30 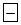 |
Имеется единственная клетка, для которой величина положительна 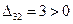 . Поэтому план не оптимален. Проведем перераспределение поставок. Построим прямоугольник перераспределения. Он проходит через четыре клетки. Расставив знаки вершин прямоугольника, найдем минимальную поставку среди отрицательных вершин. В данном случае она равна
. Поэтому план не оптимален. Проведем перераспределение поставок. Построим прямоугольник перераспределения. Он проходит через четыре клетки. Расставив знаки вершин прямоугольника, найдем минимальную поставку среди отрицательных вершин. В данном случае она равна 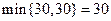 . После перераспределения новый план поставок имеет вид.
. После перераспределения новый план поставок имеет вид.
План оказался вырожденным, поэтому одну из двух исчезнувших поставок в прямоугольнике перераспределения мы делаем фиктивной (то есть пишем в клетку 0 и считаем ее фиктивно занятой). После этого пересчитываем систему потенциалов 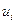 ,
, 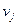 , и находим величины
, и находим величины 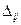 для незанятых клеток.
для незанятых клеток.
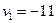 | 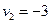 | 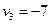 | 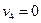 | 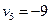 | |
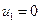 | -11 | -10 | -14 | ||
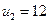 | -9 | -6 | |||
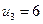 | -13 | -8 | -3 |
Теперь все величины 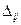 отрицательны и план поставок оптимален. Мы можем определить его стоимость
отрицательны и план поставок оптимален. Мы можем определить его стоимость 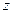 по формуле
по формуле 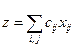 :
:
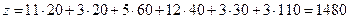 .
.
 2015-05-13
2015-05-13 918
918








