Механические колебания
Уравнение гармонических колебаний 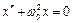 , где
, где 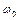 - собственная частота колебаний системы. Решение уравнения имеет вид
- собственная частота колебаний системы. Решение уравнения имеет вид 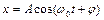 , где
, где 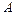 - амплитуда,
- амплитуда, 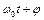 - фаза,
- фаза, 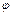 - начальная фаза колебаний.
- начальная фаза колебаний.
Периоды колебаний маятников: математического - 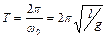 ; пружинного -
; пружинного - 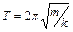 ; физического -
; физического - 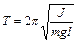 .
.
Уравнение затухающих колебаний 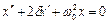 , где
, где 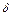 - коэффициент затухания. Решение уравнения имеет вид
- коэффициент затухания. Решение уравнения имеет вид 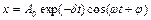 , где
, где 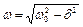 - частота затухающих колебаний.
- частота затухающих колебаний.
Логарифмический декремент затухания  обратен числу колебаний системы, в течение которых амплитуда колебаний уменьшается в
обратен числу колебаний системы, в течение которых амплитуда колебаний уменьшается в 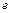 раз. Добротность
раз. Добротность 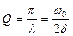 пропорциональна числу колебаний, совершаемых системой за время релаксации
пропорциональна числу колебаний, совершаемых системой за время релаксации 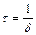 .
.
Уравнение вынужденных колебаний 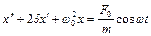 , где
, где 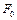 и
и 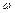 - амплитуда и частота внешней вынуждающей силы. Решение этого уравнения равно сумме решений однородного уравнения (затухающих колебаний) и частного решения неоднородного уравнения, которое имеет вид
- амплитуда и частота внешней вынуждающей силы. Решение этого уравнения равно сумме решений однородного уравнения (затухающих колебаний) и частного решения неоднородного уравнения, которое имеет вид 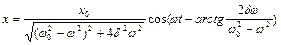 .
.
Резонансная частота и амплитуда вычисляются по формулам 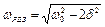 ,
, 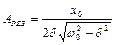 .
.
При сложении двух гармонических колебаний одинакового направления и частоты 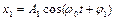 и
и 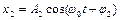 получается результирующее колебание
получается результирующее колебание 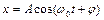 , амплитуда и начальная фаза которого вычисляется по формулам
, амплитуда и начальная фаза которого вычисляется по формулам 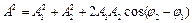 ,
, 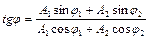 .
.
 2015-05-13
2015-05-13 241
241







