1.6.1. Материальная точка совершает колебания согласно уравнению 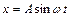 . В какой-то момент времени смещение точки
. В какой-то момент времени смещение точки 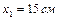 . При возрастании фазы колебаний в два раза смещение
. При возрастании фазы колебаний в два раза смещение 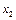 оказалось равным
оказалось равным 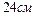 . Определить амплитуду колебаний
. Определить амплитуду колебаний 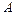 . Ответ:
. Ответ: 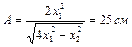 .
.
1.6.2. Материальная точка, совершающая гармонические колебания с частотой 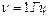 , в момент времени
, в момент времени 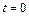 проходит положение, определяемое координатой
проходит положение, определяемое координатой 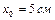 , со скоростью
, со скоростью 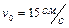 . Определить амплитуду колебаний. Ответ:
. Определить амплитуду колебаний. Ответ: 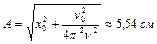 .
.
1.6.3. Полная энергия 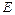 гармонически колеблющейся точки равна 10 мкДж, а максимальная сила, действующая на точку
гармонически колеблющейся точки равна 10 мкДж, а максимальная сила, действующая на точку 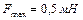 . Напишите уравнение движения этой точки
. Напишите уравнение движения этой точки 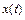 , если период
, если период 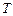 колебаний равен 4 с, а начальная фаза
колебаний равен 4 с, а начальная фаза 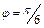 . Ответ:
. Ответ: 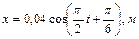 .
.
1.6.4. Если увеличить массу груза, подвешенного к пружине, на 600 г, то период колебаний груза возрастает в 2 раза. Определить массу первоначально подвешенного груза. Ответ: 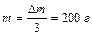 .
.
1.6.5. На горизонтальной пружине жесткостью 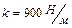 укреплен шар массой
укреплен шар массой 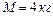 , лежащий на гладком столе, по которому он может скользить без трения. Пуля массой
, лежащий на гладком столе, по которому он может скользить без трения. Пуля массой 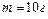 , летящая с горизонтальной скоростью
, летящая с горизонтальной скоростью 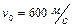 и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1)амплитуду колебаний шара; 2)период колебаний шара. Ответ:
и имеющая в момент удара скорость, направленную вдоль оси пружины, попала в шар и застряла в нем. Пренебрегая массой пружины и сопротивлением воздуха, определить: 1)амплитуду колебаний шара; 2)период колебаний шара. Ответ: 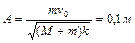 ,
, 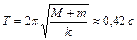 .
.
1.6.6. На чашку весов массой 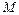 , подвешенную на пружине жесткостью
, подвешенную на пружине жесткостью 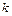 , с высоты
, с высоты 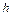 падает небольшой груз массой
падает небольшой груз массой 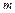 . Удар груза о дно чашки является абсолютно неупругим. Чашка в результате падения груза начинает совершать колебания. Определить амплитуду этих колебаний. Ответ:
. Удар груза о дно чашки является абсолютно неупругим. Чашка в результате падения груза начинает совершать колебания. Определить амплитуду этих колебаний. Ответ: 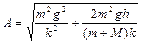 .
.
1.6.7. Физический маятник представляет собой тонкий однородный стержень длиной 35 см. Определить, на каком расстоянии от центра масс должна находиться точка подвеса, чтобы частота колебаний была максимальной. Ответ: 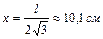 .
.
1.6.8. Однородный диск радиусом 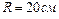 колеблется около горизонтальной оси, проходящей на расстоянии
колеблется около горизонтальной оси, проходящей на расстоянии 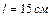 от центра диска. Определить период колебаний диска относительно этой оси. Ответ:
от центра диска. Определить период колебаний диска относительно этой оси. Ответ: 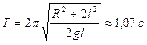 .
.
1.6.9. Тонкий обруч радиусом 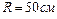 подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определить период колебаний обруча. Ответ:
подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определить период колебаний обруча. Ответ: 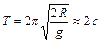 .
.
1.6.10. Тонкий однородный стержень длиной 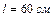 может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии
может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии 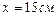 от его середины. Определить период колебаний стержня, если он совершает малые колебания. Ответ:
от его середины. Определить период колебаний стержня, если он совершает малые колебания. Ответ: 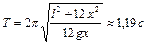 .
.
1.6.11 Из тонкого однородного диска радиусом 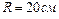 вырезана часть, имеющая форму круга радиусом
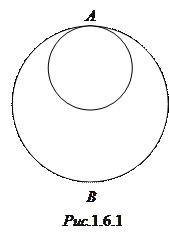
вырезана часть, имеющая форму круга радиусом 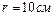 , центр которого находится на середине радиуса диска (рис.1.6.1). Определить периоды колебаний получившегося маятника относительно горизонтальных осей, проходящих через образующие диска в точках А и В.
, центр которого находится на середине радиуса диска (рис.1.6.1). Определить периоды колебаний получившегося маятника относительно горизонтальных осей, проходящих через образующие диска в точках А и В.
 |
Ответ:
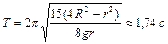 ,
, 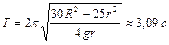 .
. 1.6.12. Математический маятник отклонили на 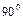 от вертикали и отпустили. В тот момент, когда маятник проходил положение равновесия, точка его подвеса стала двигаться вверх с ускорением
от вертикали и отпустили. В тот момент, когда маятник проходил положение равновесия, точка его подвеса стала двигаться вверх с ускорением 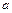 . На какой максимальный угол от вертикали отклонится маятник? Ответ:
. На какой максимальный угол от вертикали отклонится маятник? Ответ: 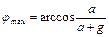 .
.
1.6.13. Математический маятник, состоящий из нити длиной 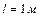 и свинцового шарика радиусом
и свинцового шарика радиусом 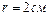 , совершает гармонические колебания с амплитудой
, совершает гармонические колебания с амплитудой 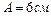 . Определить: 1)скорость шарика в момент прохождения им положения равновесия; 2)максимальное значение возвращающей силы. Плотность свинца
. Определить: 1)скорость шарика в момент прохождения им положения равновесия; 2)максимальное значение возвращающей силы. Плотность свинца 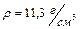 . Ответ:
. Ответ: 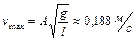 ,
, 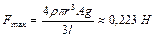 .
.
1.6.14. Математический маятник длиной 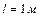 подвешен к потолку кабины, которая начинает опускаться вертикально вниз с ускорением
подвешен к потолку кабины, которая начинает опускаться вертикально вниз с ускорением 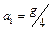 . Спустя время
. Спустя время 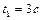 после начала движения кабина начинает двигаться равномерно, а затем в течение 3 с тормозится до остановки. Определить периоды гармонических колебаний маятника на каждом участке пути. Ответ:
после начала движения кабина начинает двигаться равномерно, а затем в течение 3 с тормозится до остановки. Определить периоды гармонических колебаний маятника на каждом участке пути. Ответ: 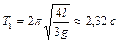 ,
, 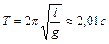 ,
, 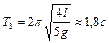 .
.
1.6.15. К наклонной стене подвешен маятник длины 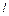 . Маятник отклонили от вертикали на малый угол, в два раза превышающий угол наклона стены к вертикали, и отпустили. Найти период колебаний маятника, если удары о стену абсолютно упругие. Ответ:
. Маятник отклонили от вертикали на малый угол, в два раза превышающий угол наклона стены к вертикали, и отпустили. Найти период колебаний маятника, если удары о стену абсолютно упругие. Ответ: 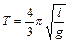 .
.
1.6.16. Тело массы 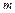 , подвешенное на пружине жесткости
, подвешенное на пружине жесткости 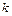 , лежит на подставке. Подставку мгновенно убирают. Написать уравнение колебаний тела
, лежит на подставке. Подставку мгновенно убирают. Написать уравнение колебаний тела 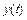 , если первоначально пружина не деформирована. Ответ:
, если первоначально пружина не деформирована. Ответ: 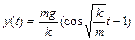 .
.
1.6.17. Складываются два гармонических колебания одного направления, уравнения которых 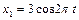 и
и 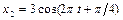 , см. Определить амплитуду и начальную фазу результирующего колебания. Ответ:
, см. Определить амплитуду и начальную фазу результирующего колебания. Ответ:
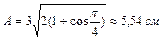 ,
, 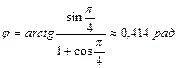 .
.
1.6.18. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях согласно уравнениям 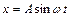 и
и 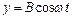 . Определить уравнение траектории точки
. Определить уравнение траектории точки 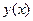 и указать направление движения точки по ней. Ответ:
и указать направление движения точки по ней. Ответ: 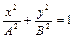 , по часовой стрелке.
, по часовой стрелке.
1.6.19. Точка участвует в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях согласно уравнениям 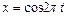 и
и 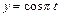 . Определить уравнение траектории точки
. Определить уравнение траектории точки 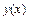 . Ответ:
. Ответ: 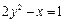 .
.
1.6.20. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях согласно уравнениям 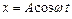 и
и 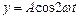 . Определить уравнение траектории точки
. Определить уравнение траектории точки 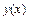 . Ответ:
. Ответ: 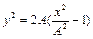 .
.
1.6.21. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 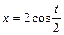 и
и 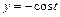 . Определить уравнение траектории точки
. Определить уравнение траектории точки 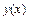 . Ответ:
. Ответ: 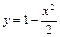 .
.
1.6.22. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 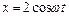 и
и 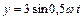 . Определить уравнение траектории точки
. Определить уравнение траектории точки 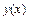 . Ответ:
. Ответ: 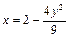 .
.
1.6.23. Амплитуда затухающих колебаний маятника за 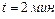 уменьшилась в 2 раза. Определить коэффициент затухания
уменьшилась в 2 раза. Определить коэффициент затухания 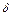 .
. 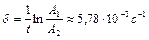 .
.
1.6.24. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 3 раза. Определить, во сколько раз она уменьшится за 4 мин. Ответ: 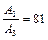 .
.
1.6.25. Начальная амплитуда затухающих колебаний маятника 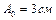 . По истечении
. По истечении 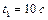 амплитуда становится
амплитуда становится 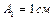 . Определить, через какое время от начала колебаний амплитуда станет
. Определить, через какое время от начала колебаний амплитуда станет 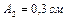 . Ответ:
. Ответ: 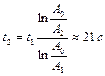 .
.
1.6.26. Тело массой 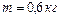 , подвешенное к пружине жесткостью
, подвешенное к пружине жесткостью 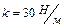 , совершает в некоторой среде упругие колебания. Логарифмический декремент колебаний
, совершает в некоторой среде упругие колебания. Логарифмический декремент колебаний 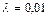 . Определить: 1) время, за которое амплитуда колебаний уменьшится в 3 раза; 2)число полных колебаний, которые должно совершить тело за это время. Ответ:
. Определить: 1) время, за которое амплитуда колебаний уменьшится в 3 раза; 2)число полных колебаний, которые должно совершить тело за это время. Ответ: 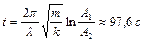 ,
, 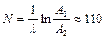 .
.
1.6.27. При наблюдении затухающих колебаний выяснилось, что для двух последовательных колебаний амплитуда второго меньше амплитуды первого на 60%. Период затухающих колебаний 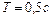 . Определить, какова была бы при этих условиях частота незатухающих колебаний. Ответ:
. Определить, какова была бы при этих условиях частота незатухающих колебаний. Ответ: 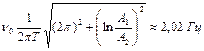 .
.
1.6.28. Тело массой 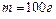 , совершая затухающие колебания, за
, совершая затухающие колебания, за 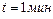 потеряло 40% своей энергии. Определить коэффициент сопротивления
потеряло 40% своей энергии. Определить коэффициент сопротивления 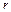 . Ответ:
. Ответ: 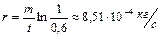 .
.
1.6.29. Гиря массой 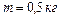 , подвешенная на пружине жесткостью
, подвешенная на пружине жесткостью 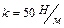 совершает колебания в вязкой среде с коэффициентом сопротивления
совершает колебания в вязкой среде с коэффициентом сопротивления 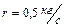 . На верхний конец пружины начинает действовать вынуждающая сила, изменяющаяся по закону
. На верхний конец пружины начинает действовать вынуждающая сила, изменяющаяся по закону 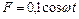 . Определить для данной колебательной системы резонансную амплитуду. Ответ:
. Определить для данной колебательной системы резонансную амплитуду. Ответ: 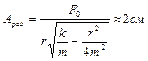 .
.
1.6.30. Гиря массой 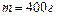 , подвешенная на пружине жесткостью
, подвешенная на пружине жесткостью 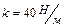 , опущена в масло. Коэффициент сопротивления для этой системы
, опущена в масло. Коэффициент сопротивления для этой системы 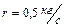 . На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону
. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону 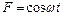 . Определить амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний. Ответ:
. Определить амплитуду вынужденных колебаний, если частота вынуждающей силы вдвое меньше собственной частоты колебаний. Ответ: 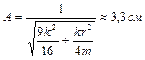 .
.
 2015-05-13
2015-05-13 1050
1050
