Решение задачи о распространении тепла в бесконечном стержне

Допущение: боковая поверхность теплоизолирована.

Задача: Найти ограниченную функцию

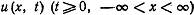, удовлетворяющую уравнению теплопроводности:

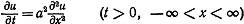, (1)

и нач. условию: 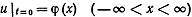(2), где φ(х) – непрерывная ограниченная функция.

По методу Фурье: 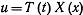(3)

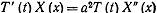
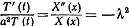
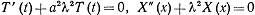
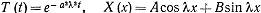
Постоянные А и В могут зависить от λ. Так как граничные условия отсутствуют, то параметр λ остается совершенно произвольным. Согласно (3) получим:

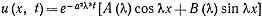(4)

-частное решение уравнения (1) при любых А(λ) и В(λ).

Интегрируя (4) по параметру λ, также получим решение уравнения (1).

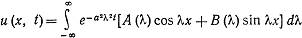(5)

Выберем А(λ) и В(λ), так чтобы выполнялось начальное условие (2): 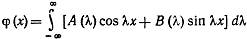(6)

получим:

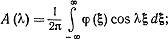
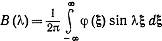
Подставляя (7) в (5):

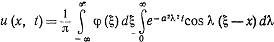
Проведя сложные вычисления получим:

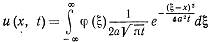
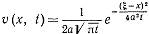- фундаментальное решение уравнения теплопроводности.