Основные понятия математической физики. Классификация линейных уравнений с часными производными второго порядка относительно функции двух переменных

Ряд Фурье в комплексной форме.

Выражение 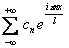называется комплексной формой ряда Фурье функции f (x), если 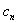определяется равенством

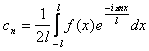, где 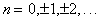Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:

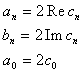(n =1,2,...)

Интеграл Фурье в действительной форме.

Интеграл Фурье для кусочно-непрерывной и абсолютно интегрируемой на 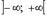функции f:

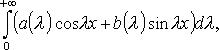где 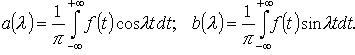11.Интеграл Фурье для четных и нечетных функций

Если f четная, то 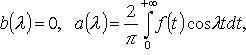интеграл Фурье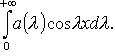

Если f нечетная, то 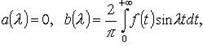интеграл Фурье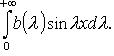

Интеграл Фурье в комплексной форме. Преобразование Фурье.

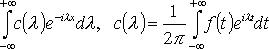
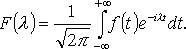или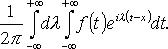

Преобразование Фурье функции f

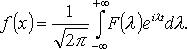
Обратное преобразование Фурье

Основные понятия математической физики. Классификация линейных уравнений с часными производными второго порядка относительно функции двух переменных.

ДУ в частных производных называется соотношение, связывающее независимые переменные, искомые функции и ее частные производные.

Наивысший порядок производной, входящей в уравнение наз. порядком ДУ.

Уравнения в частных производных также имеют бесконечное множество решений. Однако оно в своем решении имеет не производную константы, а производную функции.

u_xy= 0, u_x=С+φ(х), u=Cx+∫φ(x)dx+ψ(y)

φ(х) – некоторая производная функция от х

ψ(y) -некоторая производная функция от у

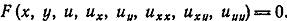
Уравнение называется квазилинейным относительно старших производных, если оно имеет вид:

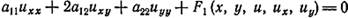
где а₁₁,а ₁₂,а ₂₂ являются функциями х и у.

Обозначим за ▲= а ₁₂²-а₁₁ а ₂₂ – (дискриминанта)

Уравнение будет называться в т. М области ХОУ:

1) Гиперболического типа, если в т. М ▲>0;

2) Параболического типа, если в т. М ▲=0;

3) Элептического типа, если в т. М ▲<0.

Если во всех точках некоторой области D плоскости ХОУ ▲>0, то рассматриваемое уравнение в этой области называется гиперболического типа. Аналогично формулируются определения ур-ний параболического и элептического типов.

Если в одних точках области уравнение имеет один тип, а в других точках другой тип, то во всей области уравнение наз. уравнением смешанного типа. Тип уравнения не меняется при преобразовании уравнения с помощью замены переменных.

Уравнение называется линейным, если оно линейно как относительно старших производных u_xx, u_xy, u_yy, так и относительно функции u и ее первых производных u_x, u_y.

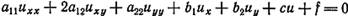
Уравнения 2 порядка играют особую роль в физике и технике, т.к. они выражают законы сохранения некоторых величин (массы, энергии, кол-ва движения и т.д.), изменения которых выражаются во многих случаях через производные 1 и 2 порядка.

Опр: Решением ДУ наз. такая функция u(x,y), которая при подстановке в уравнение обращает его в тождество.