Решение задачи о свободных колебаниях бесконечной струны. Формула Деламбера

Задача Дирехле для уравнения Лапласа в прямоугольнике.

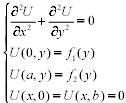
-Гармоническая функция

;

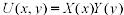
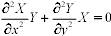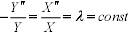
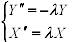Если брать λ<0, мы получим решение уравнения равное постоянной, а это не удовлетворяет условиям.

Пусть λ>0, например λ=р²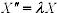

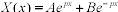- решение уравнения.

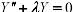
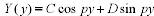-решение уравнения

Удовлетворим граничным условиям:

; ;

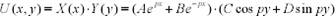
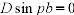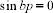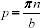
Запишем решение:

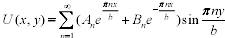(1)

Удовлетворим начальным условиям: 1)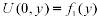

;

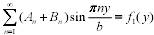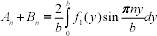
2)

;

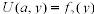
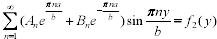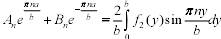
Для нахождения коэффициентов А и В необходимо решить систему: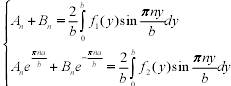

Подставив полученные коэффициенты в уравнение (1) получим решение задачи.

Решение задачи о свободных колебаниях бесконечной струны. Формула Деламбера.

Уравнение своб. колебаний однородной струны:

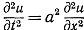(1) Положим: ;

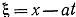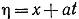
Преобразовываем уравнение колебаний к виду: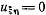

Найдем общий интеграл и получим: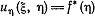

Интегрируя это равенство по ή при фиксированном ξ, получим.

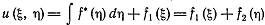
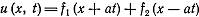(5) -общий интегралуравнения (1)

Воспользуемся начальными условиями:

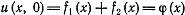
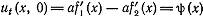(7)

Проинтегрируем (7):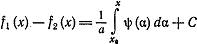

Из равенств: 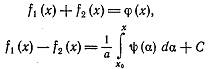находим:

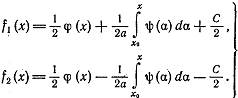
Таким образом мы определили f₂(x) и f₁(x) через заданные функции φ и ψ. Подставим в (5) значения f₂(x) и f₁(x) получим:

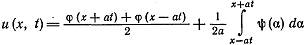
-формула Даламбера!