Установившееся движение газа в газопроводе описывается тремя уравнениями: уравнением движения, уравнение неразрывности, уравнение состояния газа.
Уравнение движения: 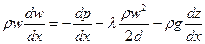 , где
, где 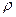 - плотность газа;
- плотность газа; 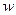 - средняя по сечению
- средняя по сечению 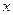 скорость газа;
скорость газа; 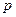 - среднее по сечению
- среднее по сечению 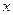 давление газа;
давление газа; 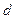 - внутренний диаметр трубопровода;
- внутренний диаметр трубопровода; 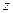 - высота сечения
- высота сечения 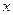 .
.
Величину 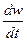 можно определить по формуле:
можно определить по формуле: 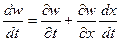 . При установившемся движении частная производная средней по сечению
. При установившемся движении частная производная средней по сечению 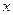 скорости газа по времени
скорости газа по времени 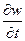 стремиться к нулю, поэтому
стремиться к нулю, поэтому 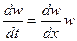 .
.
Уравнение неразрывности: 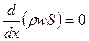 , или
, или 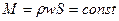 .
.
При выводе основных формул для гидравлического расчёта магистрального газопровода принимаются следующие допущения:
1. Температура постоянная, 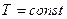 .
.
2. Коэффициент сверхсжимаемости не меняется, 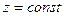 .
.
3. Коэффициент местного гидравлического сопротивления остаётся постоянным, 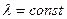 .
.
4. Величиной 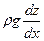 можно пренебречь, то есть
можно пренебречь, то есть 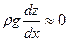 , вследствие малой плотности газа, однако этой величиной нельзя пренебрегать в случае, если проектируемый магистральный газопровод будет проходить по сильно пересечённой местности.
, вследствие малой плотности газа, однако этой величиной нельзя пренебрегать в случае, если проектируемый магистральный газопровод будет проходить по сильно пересечённой местности.
5. Величиной 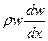 также можно пренебречь, то есть
также можно пренебречь, то есть 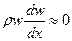 .
.
Получаем следующее уравнение движения: 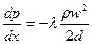 . Плотность газа можно определить по следующей формуле:
. Плотность газа можно определить по следующей формуле: 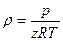 . Средняя по сечению
. Средняя по сечению  скорость газа находиться с помощью следующего уравнения:
скорость газа находиться с помощью следующего уравнения: 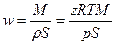 . Тогда уравнение движения примет вид:
. Тогда уравнение движения примет вид: 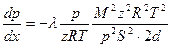 . Расписав площадь сечения
. Расписав площадь сечения 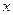 магистрального трубопровода, получим:
магистрального трубопровода, получим: 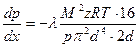 . Проинтегрируем полученное выражение по координате
. Проинтегрируем полученное выражение по координате 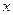 от
от 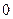 до
до 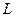 , где
, где 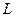 - длина трубопровода:
- длина трубопровода: 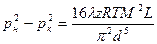 - формула падения квадрата давления по длине магистрального трубопровода. С помощью этой формулы можно получить формулу для определения массового расхода:
- формула падения квадрата давления по длине магистрального трубопровода. С помощью этой формулы можно получить формулу для определения массового расхода: 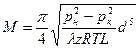 . Найдём коммерческий расход:
. Найдём коммерческий расход: 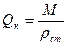 , где
, где 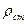 - плотность газа при стандартных условиях, которая определяется по формуле:
- плотность газа при стандартных условиях, которая определяется по формуле: 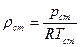 , в которой
, в которой 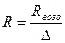 , а
, а 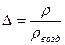 . Тогда:
. Тогда: 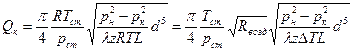 . Величину
. Величину 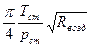 можно рассчитать:
можно рассчитать: 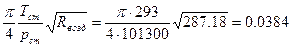 . Эта величина обозначается за
. Эта величина обозначается за 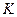 , то есть
, то есть 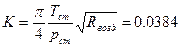 . С учётом этого выражение для определения коммерческого дебита принимает вид:
. С учётом этого выражение для определения коммерческого дебита принимает вид: 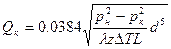 .
.
 2015-05-13
2015-05-13 2155
2155

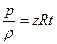 .
.






