56.
| Абсциссы кривой н.р. (т/га): | |||||||
| Ординаты кривой f(x) ∙102: | 0,15 | 1,80 | 8,07 | 13,30 | 8,07 | 1,80 | 0,15. |
57.
| Абсциссы кривой н.р. (кг/м2): | |||||||
| Ординаты кривой f(x) ∙102: | 0,06 | 0,68 | 3,02 | 5,0 | 3,02 | 0,68 | 0,06. |
58.
| Абсциссы кривой н.р. (%): | |||||||
| Ординаты кривой f(x) ∙102: | 0,22 | 2,7 | 12,1 | 19,9 | 12,1 | 2,7 | 0,22. |
59.
| Абсциссы кривой н.р. (т/га): | |||||||
| Ординаты кривой f(x) ∙102: | 0,11 | 1,35 | 6,05 | 9,97 | 6,05 | 1,35 | 0,11. |
60. а) Р (qц > 18 т/га) = 0,788;
б) Р (qц < 22 т/га) = 0,788.
61. а) Р (R > 25 %) = 0,66;
б) Р (R < 20 %) =0,0082.
62. а) Р (iобщ < 70 кг/м2) = 0,894;
б) Р (iобщ > 50 кг/м2) = 0,894.
63. а) Р (hос < 80 кг/м2) = 0,996;
б) Р (hос > 50 кг/м2) = 0,802.
64. 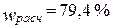 .
.
65. а) 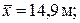
б) 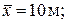
в) 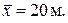
66. а) 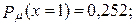
б) 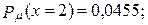
в) 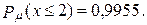
67. а) 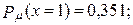
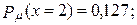
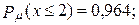
б) 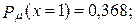
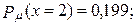
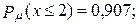
в) 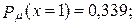
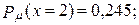
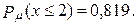
68. а) 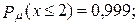
б) 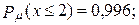
в) 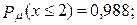
г) 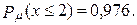
69. 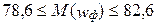 .
.
70. Доверительный интервал (надежность 0,95) для математического ожидания месячной нормы осадков (кг/м2):
в Вологодской области: май 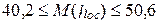 ;
;
июнь 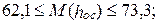 июль
июль 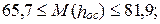
август 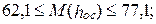
в Горьковской (Нижегородской) области: май 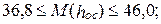
июнь 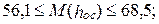 июль
июль 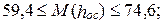
август 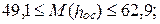
в Ивановской области: май 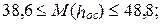
июнь 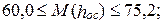 июль
июль 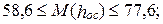
август 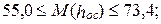
в Калининской (Тверской) области: май 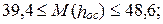
июнь 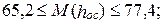 июль
июль 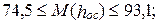
август 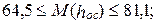
в Ленинградской области: май 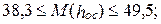
июнь 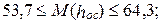 июль
июль 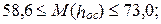
август 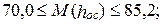
в Московской области: май 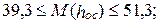 июнь
июнь 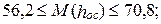
июль 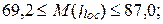 август
август 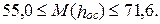
71. 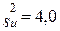 .
.
72. Подлежат браковке 10,9% продукции.
73. 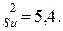
74. 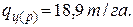
75. 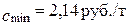 .
.
76. Надежность прогнозов по содержанию углерода в низинных торфах:
а) 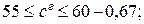
б) 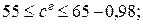
в) Сг > 60 % = 0,31; г) Сг < 62 % = 0,93.
77. 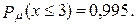
78. а) Р μ (х < 3) = 0,92;
б) 0,632.
79. 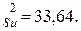
80. 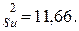
81. 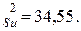
82. n = 61.
83. 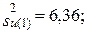
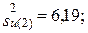 Fрасч. = 1,027; Fтабл (0,05; f1 = 9; f2 =9) = 3,18. Так как Fрасч. < Fтабл, дисперсии в статистическом смысле равны.
Fрасч. = 1,027; Fтабл (0,05; f1 = 9; f2 =9) = 3,18. Так как Fрасч. < Fтабл, дисперсии в статистическом смысле равны.
84. 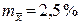 .
.
85. νрасч (α = 0,05; с = 0,34; f1 = f2 = 9) = 1,47;
νтабл (α = 0,05; с = 0,34; f1 = f2 = 9) = 2,12. Так как νрасч < νтабл, гипотеза о более высокой эффективности удобрений второго вида не принимается.
86. νрасч = 1,96; νтабл (α = 0,05; с = 0,32; f1 = f2 = 11) = 2,1. Так как νрасч < νтабл, утверждение, что первая схема позволяет получить торф более высокого качества по влажности, несостоятельно.
87. νрасч = 0,86; νтабл (α = 0,05; с = 0,45; f1 = f2 = 54) = 1,98. Так как νрасч < νтабл, различия в среднемесячной сумме осадков в августе в Калининской (Тверской) и Ленинградской областях статистически незначимы.
88. Сравнение сырьевых баз 2-х производственных объединений по степени разложения торфа: 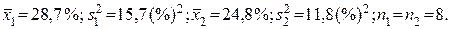 νрасч = 2,10; νтабл (α = 0,05; с = 0,43; f1 = f2 = 7) = 2,15; так как νрасч < νтабл, различия сырьевых баз двух ПО статистически незначимы.
νрасч = 2,10; νтабл (α = 0,05; с = 0,43; f1 = f2 = 7) = 2,15; так как νрасч < νтабл, различия сырьевых баз двух ПО статистически незначимы.
89. (89.1, май) λ = 0,73 < 1,36, Н0 принимается; χ2 = 4,26; 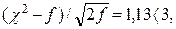 H0 принимается.
H0 принимается.
(89.2, июнь) λ = 0,305 < 1,36, Н0 принимается; χ2 = 0,95; 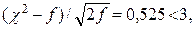 Н0 принимается.
Н0 принимается.
(89.3, июль) λ = 0,61 < 1,36, Н0 принимается; χ2 = 5,007; 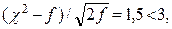 Н0 принимается.
Н0 принимается.
(89.4, август) λ = 0,79 < 1,36, Н0 принимается; χ2 = 5,81; 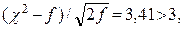 Н0 не принимается.
Н0 не принимается.
90. (90.1, май) λ = 0,92 < 1,36, Н0 принимается; χ2 = 5,587; 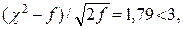 Н0 принимается.
Н0 принимается.
(90.2, июнь) λ = 0,43 < 1,36, Н0 принимается; χ2 = 5,388; 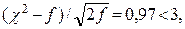 Н0 принимается.
Н0 принимается.
(90.3, июль) λ = 0,67 < 1,36, Н0 принимается; χ2 = 3,565; 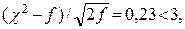 Н0 принимается.
Н0 принимается.
(90.4, август) λ = 1,28 < 1,36, Н0 принимается; χ2 = 7,94; 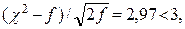 Н0 принимается.
Н0 принимается.
91. (91.1) λ = 0,32 < 1,36, Н0 принимается; χ2 = 0,79; 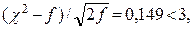 Н0 принимается.
Н0 принимается.
(91.2) λ = 0,16 < 1,36, Н0 принимается; χ2 = 0,15; 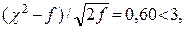 Н0 принимается.
Н0 принимается.
(91.3) λ = 0,75 < 1,36, Н0 принимается; χ2 = 5,99; 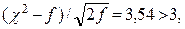 Н0 не принимается.
Н0 не принимается.
(91.4) λ = 0,316 < 1,36, Н0 принимается; χ2 = 1,294; 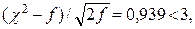 Н0 принимается.
Н0 принимается.
(91.5) λ = 0,63 < 1,36, Н0 принимается; χ2 = 3,878; 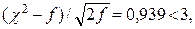 Н0 принимается.
Н0 принимается.
(91.6) λ = 0,63 < 1,36, Н0 принимается; χ2 = 4,05; 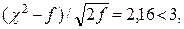 Н0 принимается.
Н0 принимается.
(91.7) λ = 0,47 < 1,36, Н0 принимается; χ2 = 1,766; 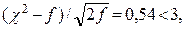 Н0 принимается.
Н0 принимается.
92. 1) метод однофакторного дисперсионного анализа: межгрупповая дисперсия 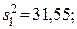 внутригрупповая дисперсия
внутригрупповая дисперсия 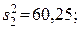 критерий Фишера F = 31,55./60,25 = 0,52; Fтабл (0,95) (f1 =3; f2 =24) =3,0, из чего следует, что влияние фактора А на конечную влажность незначимо.
критерий Фишера F = 31,55./60,25 = 0,52; Fтабл (0,95) (f1 =3; f2 =24) =3,0, из чего следует, что влияние фактора А на конечную влажность незначимо.
2) различие групповых средних в экстремальном случае;
min 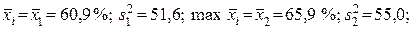 νрасч = 1,28; с = 0,48; νтабл (α = 0,05; с = 0,48; f1 = f2 = 6) = 2,18; так как νрасч < νтабл, групповые средние различаются незначимо даже в экстремальном случае.
νрасч = 1,28; с = 0,48; νтабл (α = 0,05; с = 0,48; f1 = f2 = 6) = 2,18; так как νрасч < νтабл, групповые средние различаются незначимо даже в экстремальном случае.
93. Однофакторный дисперсионный анализ: межгрупповая дисперсия 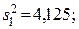 внутригрупповая дисперсия
внутригрупповая дисперсия 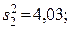 критерий Фишера F = 4,125 /4,03 = 1,024; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Гипотеза о равенстве влажности фрезеруемого слоя торфяной залежи по длине поля принимается.
критерий Фишера F = 4,125 /4,03 = 1,024; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Гипотеза о равенстве влажности фрезеруемого слоя торфяной залежи по длине поля принимается.
94. Однофакторный дисперсионный анализ: межгрупповая дисперсия 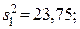 внутригрупповая дисперсия
внутригрупповая дисперсия 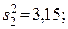 критерий Фишера F = 23,75 /3,15 = 7,54; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Фактор местоположения (начало, середина, конец поля) – значим: F = 7,54 > Fтабл(0,95) (f1 =2; f2 = 12) =3,89.
критерий Фишера F = 23,75 /3,15 = 7,54; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Фактор местоположения (начало, середина, конец поля) – значим: F = 7,54 > Fтабл(0,95) (f1 =2; f2 = 12) =3,89.
95. Однофакторный дисперсионный анализ: межгрупповая дисперсия 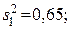 внутригрупповая дисперсия
внутригрупповая дисперсия 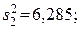 критерий Фишера F = 0,65./6,285 = 0,103; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Н0 принимается, так как F > Fтабл(0,95).
критерий Фишера F = 0,65./6,285 = 0,103; Fтабл(0,95) (f1 =2; f2 = 12) =3,89. Н0 принимается, так как F > Fтабл(0,95).
96. νрасч = 6,33; с = 0,42; νтабл (α = 0,05; с = 0,42; f1 = f2 = 5) = 2,25; νрасч > νтабл,следовательно средние значения уборочной влажности на уплотненном и неуплотненном слое торфяной залежи различаются значимо.
97. Критерий Фишера F = 35/12 = 2,92; Fтабл(0,95) (f1 = 9; f2 = 14) =2,65; F > Fтабл(0,95), следовательно, дисперсии различаются значимо.
98. Критерий Фишера F = 1169,6./1082,4 = 1,08;
Fтабл(0,95) (f1 = 54; f2 = 54) = 1,60; F < Fтабл(0,95), следовательно, дисперсии показателей месячных сумм осадков в Калининской (Тверской) и Московской областях в июле по многолетним данным различаются незначимо.
99. rух = – 0,939; mr = 0,122; tr = 7,7.
100. rух = 0,977; mr = 0,075; tr = 13,0.
101. rух = 0,929; mr = 0,131; tr = 7,1.
102. rух = 0,628; mr = 0,275; tr = 2,28.
103. rух = 0,761; mr = 0,229; tr = 3,32.
104. (104.1) у = – 27,6 + 1,152 х ± 14,4.
(104.2) у = – 53,7 + 1,877 х ± 8,5.
(104.3) у = – 4,56 + 0,786 х ± 9,3.
(104.4) у = – 37 + 1,423 х ± 5,2.
(104.5) у = – 58,7 + 1,716 х ± 8,5.
(104.6) у = 4,95 + 0,4915 х ± 5,4.
(104.7) у = – 56 + 1,753 х ± 10,4.
(104.8) у = – 15,2 + 1,141 х ± 7,4.
(104.9) у = – 28,7 + 1,272 х ± 6,2.
105. (105.1) у = – 55,7 + 1,37 х ± 7,3.
(105.2) у = – 49,4 + 1,295 х ± 8,2.
(105.3) у = – 5,2 + 0,667 х ± 7,9.
(105.4) у = – 45,9 + 1,286 х ± 9,6.
(105.5) у = – 73,8 + 1,577 х ± 6,4.
(105.6) у = – 40,2 + 1,252 х ± 8,3.
(105.7) у = – 22,4 + 0,859 х ± 11,45.
(105.8) у = – 67,3 + 1,5 х ± 9,8.
(105.9) у = – 32,4 + 1,126 х ± 8,2.
106. См. ответы к задачам (104.1) – (104.9).
107. См. ответы к задачам (105.1) – (105.9).
108. (108.1) rух = 0,884; у = – 19 + 0,884 х ± 9,3.
(108.2) rух = 0,942; у = – 38,7 + 0,987 х ± 7,9.
(108.3) rух = 0,895; у = – 102 + 1,58 х ± 16,9.
(108.4) rух = 0,90; у = – 74,7 + 1,224 х ± 13,4.
(108.5) rух = 0,892; у = – 70,3 + 1,242 х ± 11,7.
(108.6) rух = 0,724; у = – 47,25 + 0,958 х ± 19,4.
109. (109.1) rух = 0,337; у = – 3,85 + 0,617 х ± 19.
(109.2) rух = 0,89; у = – 75,8 + 1,275 х ± 12,7.
(109.3) rух = 0,892; у = – 55,6 + 1,146 х ± 12,4.
(109.4) rух = 0,975; у = – 112 + 1,61 х ± 7,9.
(109.5) rух = 0,963; у = – 80,8 + 1,35 х ± 7,1.
(109.6) rух = 0,902; у = – 49,6 + 1,052 х ± 12,7.
(109.7) rух = 0,936; у = – 65,8 + 1,2 х ± 10,9.
(109.8) rух = 0,927; у = – 76,4 + 1,27 х ± 12,1.
(109.9) rух = 0,744; у = – 33,8 + 0,931 х ± 14,3.
110. ηух = 0,676; у = 68,6 ─ 1,223 х + 0,0103 х 2.
111. ηух = 0,532; r ух = – 0,37; у = 81,8 – 0,294 х ± 24,6.
112. ηух = 0,607; m η = 0,115; t η = 5,28.
113. а). Связь у = f(x, z) для Ленинградской области в июле Rухz = 0,965;
у = – 22 + 0,923 х – 0,19 z ± 5,45.
б). Связь у = f(x, z) для Калининской (Тверской) области в июле Rухz = 0,921; у = – 0,5 + 0,772 х – 0,272 z ± 12,1.
в). Связь у = f(x, z) для Московской области в июле Rухz = 0,976;
у = 17,9 + 0,718 х – 0,392 z ± 5,9.
114. Связь у = f(x, z) для Московской области в июне Rухz = 0,963;
у = 11,5 + 1,056 х – 0,865 z ± 5,4.
115.1. rух = – 0,982; у = 60,6 – 1,23 х ± 1,9; х = 48,1 – 0,783 у ± 1,5.
115.2. rух = – 0,993; у = 58,1 – 0,952 х ± 0,77; х = 60,5 – 1,036 у ± 0,8.
115.3. rух = – 0,940; у = 58,7 – 0,95 х ± 2,26; х = 61,7 – 1,052 у ± 2,53.
115.4. rух = – 0,966; у = 54,8 – 0,832 х ± 1,52; х = 62,9 – 1,12 у ± 1,76.
115.5. rух = – 0,958; у = 53,2 – 0,786 х ± 1,47; х = 64,0 – 1,167 у ± 1,79.
115.6. rух = – 0,925; у = 59 – 0,946 х ± 2,93; х = 56,6 – 0,905 у ± 2,86.
115.7. rух = – 0,991; у = 60,9 – 1,16 х ± 1,15; х = 51,9 – 0,846 у ± 0,98.
115.8. rух = – 0,889; у = 54 – 0,788 х ± 2,85; х = 58,9 – 1,003 у ± 3,2.
116. Реализации значений показателей  рассчитывают по формуле
рассчитывают по формуле 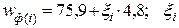 принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты расчета округляют до десятых.
принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты расчета округляют до десятых.
117. Реализации значений показателей 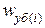 рассчитывают по формуле
рассчитывают по формуле 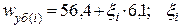 принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты расчета округляют до десятых.
принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты расчета округляют до десятых.
118. Реализации значений промежутков между пнями в торфяной залежи
(при заданном значении λ = 0,067 м-1) рассчитывают по формуле 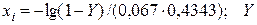 – двухзначные равномерно распределенные случайные числа на интервале (0,1) по табл. П.1.9. Значения хi округлять до десятых.
– двухзначные равномерно распределенные случайные числа на интервале (0,1) по табл. П.1.9. Значения хi округлять до десятых.
119. Реализации значений показателей 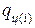 рассчитывают по формуле
рассчитывают по формуле 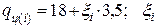 принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты округляют до десятых.
принимают по таблице нормально распределенных случайных чисел (табл. П.1.10). Результаты округляют до десятых.
120. Модель вида у = а + bx + cx2 ± mух – метод средних:
у = 1304 ─ 727 х + 187 х2 ± 30,7.
121. Линейная модель вида у = а + bx ± mух – метод средних:
у = 45,5 + 2,35 х ± 17,2.
Нелинейная модель вида у = а + bx + cx2 ± mух – метод средних:
у = 27 + 4,25 х ─ 0,0348 х2 ± 15.
122. Модель вида у = а + bx ± mух – метод средних: у = 11,8 +1,8 х ± 21,2.
123. Модель вида у = b/(1+а ехр(-кbt)); у = 130/(1 + 17,6 eхр (– 0,19 t)).
124. Модель вида у = а екt; у = 1,525 е 0,133 t.
125. Модель вида у = а екt; у = 7,52 е 0,0428 t.
126. с = f (Q), с min при Q= 1,03; 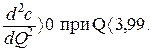
127. у = f (Q), уmin при Q= 24,6; 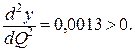
128. 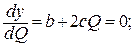
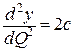 >0 при с> 0. В точке
>0 при с> 0. В точке 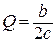 – минимум.
– минимум.
129. 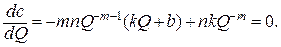 Отсюда
Отсюда 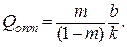
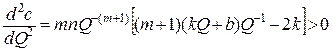 в точке Q = Qопт минимум.
в точке Q = Qопт минимум.
130. е = а lg p + b e – натуральная деформация. 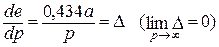 при Δ = – 0,192·10–3 и а = – 0,665;
при Δ = – 0,192·10–3 и а = – 0,665; 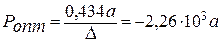 ;
;
е max= a lg p опт + b = a lg (–2,26·103 a) + b.
131. с = nN–m, 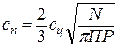 .Элементарное увеличение себестоимости транспортирования
.Элементарное увеличение себестоимости транспортирования 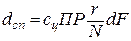 , r – расстояние перевозок. Полагая dF – элементом площади круга,
, r – расстояние перевозок. Полагая dF – элементом площади круга, 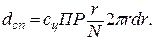 Интегрируем дифференциальное уравнение
Интегрируем дифференциальное уравнение 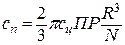 при 0 ≤ r ≤ R. Полагая район снабжения круговым с радиусом R,
при 0 ≤ r ≤ R. Полагая район снабжения круговым с радиусом R,
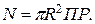 Заменив в уравнении R 3,
Заменив в уравнении R 3, 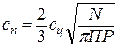 .
. 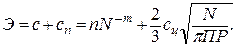
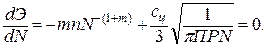
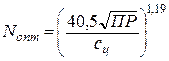 при n = 22,39 и
при n = 22,39 и
m = – 0,34.
Отсюда
h = 0; 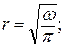
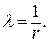
|
132. Периметр брикета l = 2 h +2 πr. Дополнительное условие ω = πr 2 +2 rh. Функция Лагранжа z = 2 h + 2 πr + λ (ω – πr 2 –2 rh).
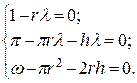
|
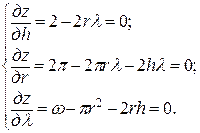
Поставленной задаче соответствует круглое сечение брикета.
133. 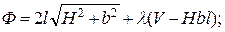


|
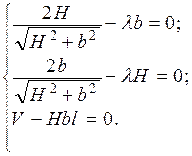
|
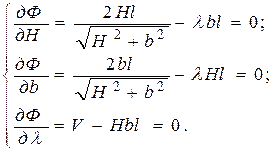
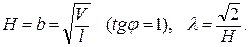
По условию 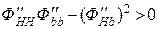 устанавливаем, что в точке Н = b минимум, так как
устанавливаем, что в точке Н = b минимум, так как 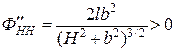 и
и 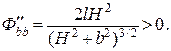
134. F = 2 π (r 2 + rh). Объем брикета V = πr 2 h. Функция Лагранжа
z = 2 π (r 2 + rh) + λ (V – πr 2 h).
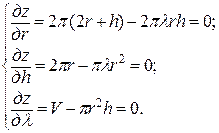
|
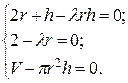
|
Отсюда 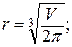 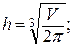
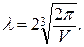
|
Методом дифференциального исчисления убедиться в том, что в найденной точке минимум. Минимальная поверхность 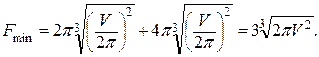
135. Ф – стоимость емкости; см – стоимость 1 см3 металла; сп – стоимость 1 см пайки; F – площадь поверхности емкости; l – длина швов пайки у одной емкости.
Минимум стоимости емкости Ф (F,l)= cмδF + cпl.
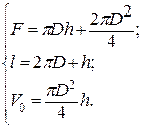
|
| Необходимо минимизировать функцию Ф (F,l) на которую налагаются связи |
Ограничения
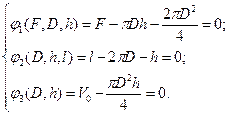
|
Функция Лагранжа и (F,D,h,l) = Ф + λ 1 φ 1 + λ 2 φ 2 + λ 3 φ 3.
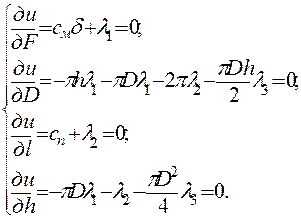
|
Из уравнения смδ + λ 1 = 0 находим λ1 = – смδ.
Из уравнения сп + λ 2 = 0 следует, что λ 2 = – сп.
Из уравнения 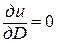 находим находим 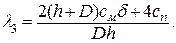 Подставляем λ1, λ2, λ3
в уравнение Подставляем λ1, λ2, λ3
в уравнение 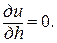
|
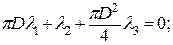
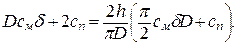 Из последнего уравнения находим h. Получаем
Из последнего уравнения находим h. Получаем 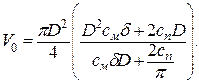
136. Необходимо минимизировать экономический критерий 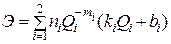 .
.
Количество поступающей сушенки в прессы 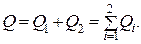
Функция Лагранжа 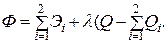
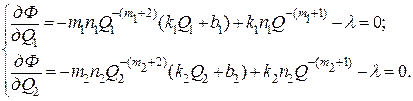
Подставим известные данные
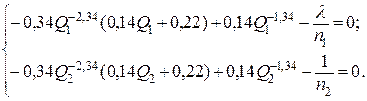
Пусть дано ограничение Q ≤ Q1 + Q2, где Q = 2 т/ч. Последнюю систему приведем к виду
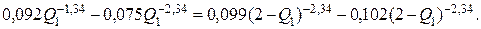
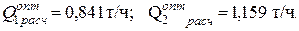
Вычтем из первого уравнения второе и заменим в нем Q2 из дополнительного условия
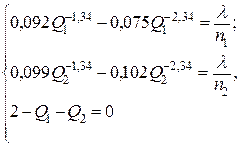
Оптимальные значения производительности прессов
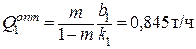 ;
; 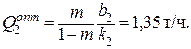
137. 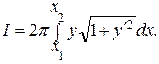 Первый интеграл Эйлера имеет вид
Первый интеграл Эйлера имеет вид 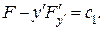
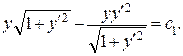
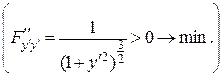 После упрощения имеем
После упрощения имеем
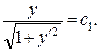 Интегрируем с помощью подстановки
Интегрируем с помощью подстановки 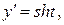 тогда
тогда 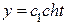 ,
,
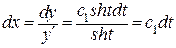 ,
, 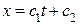 . Уравнение линии вращения в параметрической форме
. Уравнение линии вращения в параметрической форме 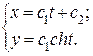
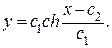
138. Поместим точку А в начало координат. Скорость материальной точки 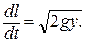 Отсюда
Отсюда 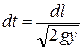 .
. 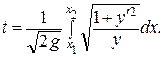
При у (0) = 0, у (х 1) = у 1, 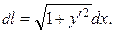 Функционал
Функционал 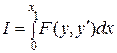 , для которого уравнение Эйлера имеет первый интеграл вида
, для которого уравнение Эйлера имеет первый интеграл вида  , или для наших условий
, или для наших условий
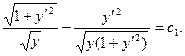 После упрощения
После упрощения 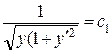 , или
, или 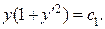
Введем параметр t, полагая у = сtgt, получим 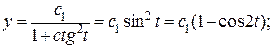
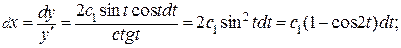
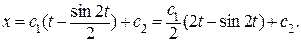 В параметрической форме уравнение имеет вид
В параметрической форме уравнение имеет вид 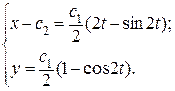
Если обозначить 2 t = t 1, а с 2 = 0 при у (0) = 0, то получим семейство циклоид
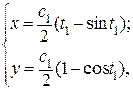
где 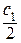 – радиус катящегося круга.
– радиус катящегося круга.
139. а) уравнение Эйлера 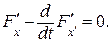
 или x = 0. Экстремаль х = 0 проходит через граничные точки только при х 1 = 0 и х 2 = 0. В этом случае экстремаль имеет минимум функционала. Если х 1 и х 2 не равны нулю, то минимума функционал не имеет.
или x = 0. Экстремаль х = 0 проходит через граничные точки только при х 1 = 0 и х 2 = 0. В этом случае экстремаль имеет минимум функционала. Если х 1 и х 2 не равны нулю, то минимума функционал не имеет.
б) уравнение Эйлера 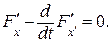
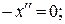 х = с 1 t + c 2. Экстремалями являются всевозможные прямые линии х = с 1 t + c 2, где с 1 и с 2 находятся из граничных условий.
х = с 1 t + c 2. Экстремалями являются всевозможные прямые линии х = с 1 t + c 2, где с 1 и с 2 находятся из граничных условий.
в) уравнение Эйлера 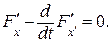
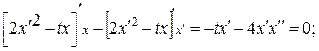
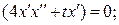
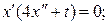
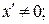
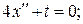
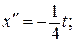
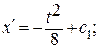
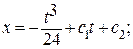 при x (0) = 0; с 1 = 0; с 2 = 0. Экстремум на кривой
при x (0) = 0; с 1 = 0; с 2 = 0. Экстремум на кривой 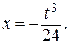
140. а) уравнение Эйлера 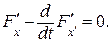
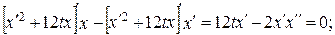

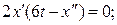
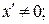
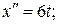
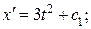
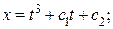 при х (0) = 0
при х (0) = 0
с 1 = 0, с 2 = 0. Экстремум на кривой х = t 3 . По условию Лежандра 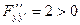 следует, что при х = t 3 заданный функционал принимает минимальное значение.
следует, что при х = t 3 заданный функционал принимает минимальное значение.
б) 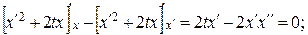
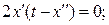
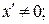
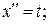
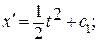
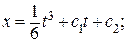 при х (0) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой
при х (0) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой 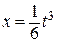 ;
;
в) 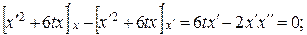
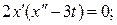
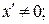
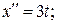
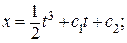 при х ()) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой
при х ()) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой 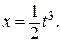
г) 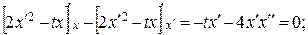
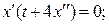
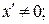
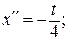
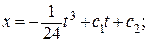 при х (0) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой
при х (0) = 0 с 1 = 0 и с 2 = 0. Экстремум на кривой 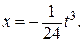
141. Составляем функцию Лагранжа 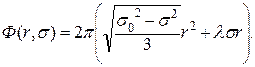 Уравнение Эйлера
Уравнение Эйлера 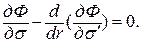 Второй член функции Лагранжа обращается в нуль.
Второй член функции Лагранжа обращается в нуль.
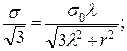
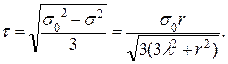
142. Максимизировать функцию S = 5 х 1 + 6 х 2 при ограничениях
| S мах = 40,5 при х 1 = 4,5; х 2 = 3. |
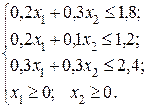
143. Максимизировать функцию S = 1 х 1 + 1 х 2 + 2 х 3 +3 х 4 при ограничениях
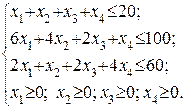
S мах = 50 при х 1 = х 2 = х 5 = х 7 = 0, х 3 = х 4 = 10 и х 6 = 50.
144 = 19550 при х 1 = 200, х 2 = 50, х 3 = 100.
145. zmin = 146690 руб. Оптимум приходится на организацию процесса с уборкой 10 валков в один штабель на площади 299 га, 12 валков – на площади 440 га и 16 валков – 261 га.
146. S мах = 23 в точке А (х,у) = А (5,4).
147. S мах = 45 в точке А (15,0); S min = 6 в точке В (0,2); S = 20,25 в точке С (3,75; 4,5).
148. S мах = 45 в точке А (15,0).
149. S мах = 13 в точке А (1,4).
150. Smin = 229 руб. при х 11 = 0,2; х 12 = 0; х 13 = 1,0; х 21 = 0,6; х 22 = 0,9; х 23 = 0, где х 11, х 12, х 13 – поставки продукции первой базой соответственно на первый, второй и третий участки; х 21, х 22, х 23 – поставки продукции второй базой соответственно на первый, второй и третий участки.
151. s = 10 x 1 + 12 x 2 →max; при ограничениях:
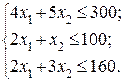
|
smax = 710 при х 1 = 35; х 2 = 30.
152. Smin = 10800 руб. при х 11 = 50 т; х 12 = 10 т; х 21 = 0; х 22 = 80 т,
где х 11, х 12, – поставки продукции с первого участка соответственно в первый и второй совхозы; х 21, х 22, – поставки продукции со второго участка соответственно в первый и второй совхозы.
153. Smin = 2560 руб. при х 11 = 2 т; х 12 = 0; х 13 = 10 т; х 21 = 6 т; х 22 = 9 т; х 23 = 0, где х 11, х 12, х 13 – поставки продукции с первой базы соответственно в первый, второй и третий магазины; х 21, х 22, х 23 – поставки продукции со второй базы соответственно в первый, второй и третий магазины.
154. Составим функцию Гамильтона 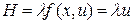 . Дифференциальное уравнение для определения
. Дифференциальное уравнение для определения 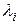 :
: 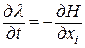 . В нашем примере это
. В нашем примере это 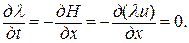 Решением
Решением 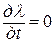 является λ = с 1 = const. Подставим значение λ в Н, получим Н = с 1 и. Оптимальное управление не зависит от времени t. Так как и опт > 0 и Н ≥ 0, то с1 > 0, а и опт = с 1 U. Подставим и опт = с 1 U в уравнение, описывающее процесс
является λ = с 1 = const. Подставим значение λ в Н, получим Н = с 1 и. Оптимальное управление не зависит от времени t. Так как и опт > 0 и Н ≥ 0, то с1 > 0, а и опт = с 1 U. Подставим и опт = с 1 U в уравнение, описывающее процесс 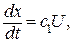 и проинтегрируем х = с 1 Ut + c 2. Из граничных условий х (t = 0) = x 0; х (t = tk) = xk определяем c2 = x 0, а
и проинтегрируем х = с 1 Ut + c 2. Из граничных условий х (t = 0) = x 0; х (t = tk) = xk определяем c2 = x 0, а 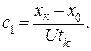 Таким образом
Таким образом 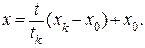 Из постоянства и опт можно принять с 1 = 1, тогда время перехода из состояния х 0 в состояние х к можно определить по формуле
Из постоянства и опт можно принять с 1 = 1, тогда время перехода из состояния х 0 в состояние х к можно определить по формуле 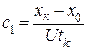 . Отсюда при с 1 = 1
. Отсюда при с 1 = 1 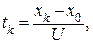 а оптимальная траектория процесса х = Ut + x 0.
а оптимальная траектория процесса х = Ut + x 0.
155. Рекомендуется отобрать пробы на влажность на пяти технологических площадках: 2-й, 4-, 6-, 8-й, 10-й от магистрального канала к противопожарному. Количество проб на площадке 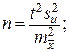
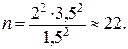 Влияние фактора местоположения площадки на показатели влажности фрезеруемого слоя оценивается по схеме однофакторного дисперсионного анализа.
Влияние фактора местоположения площадки на показатели влажности фрезеруемого слоя оценивается по схеме однофакторного дисперсионного анализа.
156. 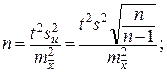 n ≈ 20.
n ≈ 20.
157. Наметить четыре уровня начальной влажности, например, 77 – 79 – 81 – 83 %. На каждом из уровней заложить четыре рамки с торфом с удельной загрузкой по сухому веществу на четырех уровнях, например 0,6 – 0,72 – 0,84 – 0,96 кг/м2; предусмотреть хотя бы минимальную повторность – 2. Всего, таким образом, должны быть заложены 4 · 4 · 2 = 32 объекта сушки.
158. ПФЭ: τс = f(Wнач, кг/кг; Рс, кг/м2)
| Факторы | Уровни | Шаг варьирования | ||
| – 1 | + 1 | |||
| х 1 (Wнач, кг/кг) | 2,5 | 3,0 | 3,5 | 0,5 кг/кг |
| х 2 (Рс, кг/м2) | 1,0 | 1,5 | 2,0 | 0,5 кг/м2 |
159. ПФЭ: В = f(Wнач, кг/кг; dк, см)
| Факторы | Уровни | Шаг варьирования | ||||
| – 1 | + 1 | |||||
| х 1 (Wнач, кг/кг) | 0,5 | 1,0 | 1,5 | 0,5 кг/кг | ||
| х 2 (dк, см) | 2 см | |||||
160. ПФЭ: τс = f(Wнач, кг/кг; R д, %; Рс, кг/м2)
| Факторы | Уровни | Шаг варьирования | ||
| – 1 | + 1 | |||
| х 1 (Wнач, кг/кг) | 2,5 | 3,0 | 3,5 | 0,5 кг/кг |
| х 2 (R д, %) | 10 % | |||
| х 3 (Рс, кг/м2) | 1,0 | 1,5 | 2,0 | 0,5 кг/м2 |
161. ПФЭ: у = f(х1, х2 х3); (х 1 – влажность, w; х2 – удельная загрузка матрицы, qуд; х3 – давление уплотнения, Руд) – охват торфа агрегацией у = 73,3 + 23 х1 + 0,9 х2; граничные условия: (65 < ω < 85 %); (0,50 < qуд < 0,60 г/см2); (0,110 < Руд < 0,260 кг/см2.
162. а) ПФЭ: зависимость γн (у) от начальной плотности фрезеруемого слоя γф (х1) и дисперсности R д (х2):
| Факторы | Уровни | Шаг варьирования | ||
| – 1 | + 1 | |||
| х 1 (γф, кг/м3) | 100 кг/м3 | |||
| х 2 (R д, %) | 5 % |
б) ПФЭ: зависимость водопоглощаемости фракции < 2 мм комплексного верхового торфа, R = 15 %, от начальной влажности (х1) w и массы навески (х2) m: в кодированном виде – у = 595 –208 х1 –34 х2; в натуральных показателях В = 1007 – 10,4 w – 22,7 m, %; граничные условия: (10 < ω < 55 %); (2 < m < 5 г).
в) ПФЭ: зависимость прочности мелкокускового торфа у от доли связующего в общей массе торфа (х1) Δр и влагосодержания смеси (х2) W: в кодированном виде у = 2,92 + 0,67 х1 – 0,38 х1х2; в натуральных показателях σсж = 0,045 Δр + 0,01, МПа; граничные условия: (50 < Δр < 80 %); (2,5 < W < 3,1 кг/кг).
163. а) Р (R 0) = 0,083; Р (R 1) = 0,1822; Р (R 2) = 0,264; Р (R 3) = 0,4708;
б) Р (R 0) = 0,0781; Р (R 1) = 0,1763; Р (R 2) = 0,257; Р (R 3) = 0,4886;
в) Р (R 0) = 0,1537; Р (R 1) = 0,2655; Р (R 2) = 0,2908; Р (R 3) = 0,290.
164. у (х) = 0,00205 х 2 – 0,13585 х + 2,9931;
а) tg 40020׳ = 0,8487;
б) tg 41040׳ = 0,8917.
165. у (х) = 0,0022 х 2 – 0,151 х + 5,16; Wкп (R =16 %) = 3,31 кг/кг; 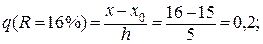 остаточный член
остаточный член 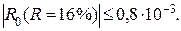 Wкп (R =17 %) = 3,23 кг/кг;
Wкп (R =17 %) = 3,23 кг/кг; 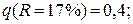
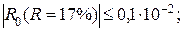 Wкп (R =22 %) = 2,90 кг/кг;
Wкп (R =22 %) = 2,90 кг/кг; 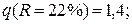
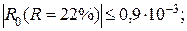 Wкп (R =27 %) = 2,69 кг/кг;
Wкп (R =27 %) = 2,69 кг/кг; 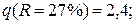
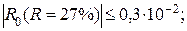
166. у (х) = 0,00075 х 2 + 1,29 х – 1,1;
τ(dн = 15 мм) = 18,4 ч; τ(dн = 30 мм) = 38,3 ч; τ(dн = 50 мм) = 65,3 ч.
167. у (х) = – 0,016276 х 3 – 0,2578125 х 2 – 0,095833 х + 2,1.
h = x i+1 – x i = 0,4; 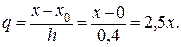
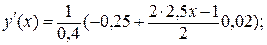
|
168. у (х) = 0,22·10–7 х 3 + 0,29898·10–4 х 2 – 0,0240685 х + 4,0.
| 169. |
| τ,ч | W, кг/кг | Δ W | Δ2 W |
| 0,4 0,8 1,2 1,6 2,0 | 2,1 1,85 1,62 1,41 1,22 1,05 | – 0,25 – 0,23 – 0,21 – 0,19 – 0,17 | 0,02 0,02 0,02 0,02 |
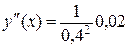 .
.
а) 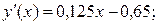
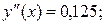 у(х) = 0,0625х2 – 0,65х + 2,1;
у(х) = 0,0625х2 – 0,65х + 2,1;
| τ, ч | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 |
б) 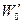
| – 0,525 | – 0,5 | – 0,475 | – 0,45 | – 0,425 | – 0,4; |
в) 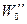
| 0,125 | 0,125 | 0,125 | 0,125 | 0,125 | 0,125. |
СОДЕРЖАНИЕ
| Введение.............................................................................................................................. 1. Методы теории вероятностей и математической статистики в торфяном производстве...................................................................................................................... 2. Статистика связей и процессов в торфяном производстве........................................ 3. Математическое моделирование в торфяном производстве...................................... 4. Методы оптимизации в торфяном производстве....................................................... 4.1. Исследование функций на экстремум....................................................................... 4.2. Метод множителей Лагранжа.................................................................................... 4.3. Вариационное исчисление........................................................................................ 4.4. Изопериметрические задачи..................................................................................... 4.5. Линейное программирование.................................................................................... 4.6. Принцип максимума................................................................................................... 5. Планирование экспериментов в торфяном производстве......................................... 6. Численные методы в торфяном производстве........................................................... 6.1. Численное решение систем линейных алгебраических уравнений....................... 6.2. Интерполирование функций...................................................................................... 6.3. Численное дифференцирование................................................................................ 6.4. Интерполяционная формула Лагранжа…………………………............................. 6.5. Тригонометрический полином……………………………………………………... 6.6.Прогнозирование циклового сбора с помощью двумерного нормального распределения ……………………………….…………………………………………... 6.7. Обоснование уровня надежности поставки торфа потребителю………………... 6.8. Проверка согласия эмпирического распределения экспоненциальному закону…………………………………………………………………………………….. 6.9. Исключение так называемых выскакивающих вариант…………………………. 6.10. Задания для самостоятельной работы …………………………………………... Приложение 1. Вспомогательные таблицы для решения приведенных в практикуме задач.................................................................................... Приложение 2. Статистический анализ данных, характеризующих метеорологические условия производства фрезерного торфа в одном из торфодобывающих регионов Российской Федерации…………………… Библиографический список…………………………………………………………….. Ответы……………………………………………………………………………………. |
 2015-05-13
2015-05-13 515
515








