Экономическая трактовка задачи линейного программирования

Имеется предприятие по производству колбасы. Мы можем выпускать 2 вида колбасы:

- вареную;

- ветчинно-рубленную.

Цена вареной колбасы 120 руб.

Цена ветчинно-рубленной – 200 руб.

Для производства этих колбас используется 3 вида рекурсов:

- говядина,

- свинина,

- горох.

На складе имеются следующие запасы этих ресурсов:

- говядина – 100 кг.,

- свинина – 60 кг.,

- горох – 200 кг.

Известны нормативы затрат каждого вида ресурса на производство единицы продукции:

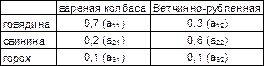
Ставится задача: Лицо, принимающее решения, должно составить план выпуска продукции, так чтобы уложиться в ограничение и обеспечить максимум стоимости выпускаемой продукции.

Введем переменные:

x – количество выпускаемой продукции,

j – номер выпускаемой продукции, j=1,2,

Тогда х_j – количество продукции j-го типа, которое мы должны определить.

b – количество ресурса, которым располагает ЛПР.

i – номер ресурса, i=1,3,

Ц_j – цена за 1 ед. j-го типа продукции,

b_i - количество ресурсов i-го типа, которыми распоряжается ЛПР,

а – норматив затрат ресурса,

а_ij – показывает сколько единиц i-го ресурса требуется для производства 1 шт. j-той продукции.

Задачи, в которых переменные и критерии и в ограничениях находятся в первой степени, называются задачами линейного программирования.

Задача в общем виде:

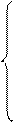
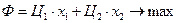
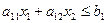- количество говядины, которая потребуется, чтобы реализовать нашу продукцию,

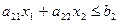- количество свинины, которая потребуется, чтобы реализовать нашу продукцию,

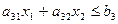- количество гороха, который потребуется, чтобы реализовать нашу продукцию.