Моделирование системы оплаты труда в бригаде из 2-х рабочих(уравнительная оплата труда)

f^* - план

1.

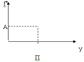
Элемент получает премию в размере А рублей, если в точности выполнит план.

2.

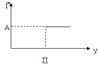
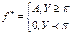
Перевыполнение плана не наказывается, но и не поощряется.

3.

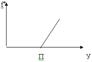
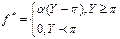
Элемент поощряется за перевыполнение плана. α – норматив премирования.

4.

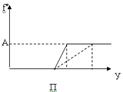
Чтобы получить еще лучший результат и увеличить объем выпуска, необходимо уменьшить норматив премирования, тогда угол наклона уменьшится. Размер вознаграждения не может превышать некоторой заданной величины А.

5.

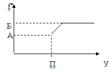
Целевая функция элемента: f (П; У) = f^* (П; У) – z (П; У).

Z – стоимостной эквивалент затрат элемента, связанный с достижением результата У.

Задача моделирования. Бригада из 2-х рабочих. Имеется плановое задание у 1 и 2 работника П₁, П₂.

Каждая штука продукции дает 1 рубль в фонд оплаты труда, т.о. ФОТ = х₁ + х₂,

х₁, х₂ - кол-во продукции, которое сделает 1 и 2-й рабочий.

Заработок: 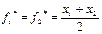. Уравнительная оплата труда. Вводим А₁ и А₂ – предельный объем продукции, который может выполнить 1-й и 2-й рабочий. С учетом этого строим функцию (А_i – x_i) – функция комфортности труда, т.е. если х = 0, то комфортность = А₁. Если рабочий будет работать, то комфортность будет = 0.

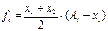- функция удовлетворенности трудом.

Пусть план 1-го рабочего = 9, 2-го – 10. А₁ = 20, А₂ = 22. Какую стратегию выберет первый рабочий?

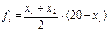
Таблица решений:

х2\х1
	104,5/114
	110/110	105/115,5
			103,5/115

Псевдо оптимальная точка
f₁ = (9+10)/2(20-9) = 104.5

f₂ = (9+10)/2(22-10) = 114

(9;10)- равновесная точка (10;11)- псевдо оптимальная

В числителе значение целевой функции для первого, а в знаменателе – для второго.

Псевдо оптимальная точка – в этой точке согласуются интересы центра и интересы элементов. Эта точка не является равновесной, т.к. у каждого элемента есть возможность улучшить свои возможности.

Первый рабочий решил снизить объем производства:

х₂ = 11, х₁ = 9

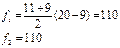
Второй, обнаружив, что у него зарплата уменьшилась, тоже уменьшит объем производства. Они вернутся в первый квадрат.