|
Рассмотрим  и рассмотрим операторы и рассмотрим операторы 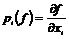 и и 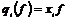 . .
Предложение. 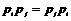 , , 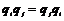 , , 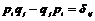 . .
Доказательство.
Первые два соотношения очевидны, докажем третье:
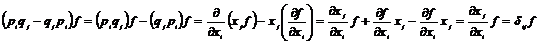 . . 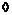
Определение. Алгеброй Вейля 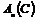 называется подалгебра с единицей в алгебре всех линейных операторов на называется подалгебра с единицей в алгебре всех линейных операторов на 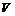 , порожденная операторами , порожденная операторами 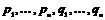 . .
Каждый элемент 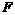 из из 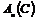 можно представить в как можно представить в как 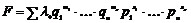 или как или как 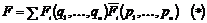 . .
Предложение. Пусть 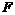 представлено в виде представлено в виде 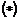 , тогда , тогда
1) 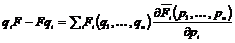
2) 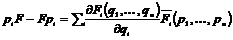
Доказательство.
В любой алгебре 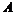 положим положим 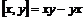 , тогда , тогда 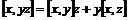 , т.е. эта операция имеет такие же свойства как и дифференцирование, будем этим пользоваться. Посчитаем , т.е. эта операция имеет такие же свойства как и дифференцирование, будем этим пользоваться. Посчитаем  - дифференцирование многочлена - дифференцирование многочлена  по переменной по переменной  : :
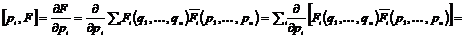
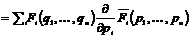 . .
Аналогично доказывает и второй пункт. 
Лекция 13 (26.11.2001)
Вернемся к рассмотрению алгебры Вейля. Напомним, что мы рассматривали пространство 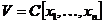 и линейные операторы и линейные операторы 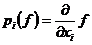 , , 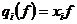 , которые обладали свойством , которые обладали свойством 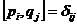 и и 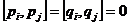 , где , где 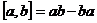 . Алгебра Вейля – это . Алгебра Вейля – это 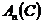 , если , если 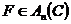 , то , то 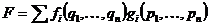 , то , то 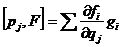 и и 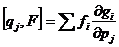 . .
Теорема. 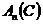 проста. проста.
Доказательство.
Пусть 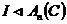 , , 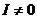 . Пусть . Пусть 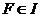 , , 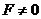 , тогда , тогда 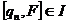 . .
Если 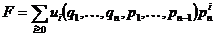 , то , то 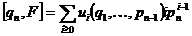 , т.е. степень , т.е. степень 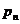 уменьшилась. Продолжая эту операцию и дальше, мы вообще избавимся от уменьшилась. Продолжая эту операцию и дальше, мы вообще избавимся от 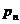 . Далее таким же образом мы можем избавиться от всех . Далее таким же образом мы можем избавиться от всех 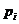 , и, рассматривая , и, рассматривая 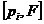 , мы можем избавиться от всех , мы можем избавиться от всех 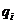 . В итоге получим, что некая константа (не нулевая) принадлежит нашему идеалу. Следовательно, т.к. константа обратима, наш идеал совпадает со всей алгеброй. Т.е. алгебра проста. . В итоге получим, что некая константа (не нулевая) принадлежит нашему идеалу. Следовательно, т.к. константа обратима, наш идеал совпадает со всей алгеброй. Т.е. алгебра проста. 
Предложение. Многочлены 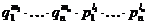 линейно независимы в линейно независимы в 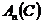 при разных при разных  . .
Доказательство.
Действительно, если 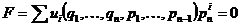 , то будем действовать аналогично доказательству предыдущей теоремы, т.е. , то будем действовать аналогично доказательству предыдущей теоремы, т.е. 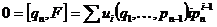 и т.д. В итоге мы получим, что ненулевая константа должна равняться нулю, что невозможно. и т.д. В итоге мы получим, что ненулевая константа должна равняться нулю, что невозможно. 
Следствие. Алгебра Вейля бесконечномерна.
Рассмотрим поле 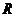 . Над . Над 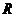 мы знаем следующие тела: мы знаем следующие тела:
1) 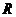 над над 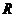 ; ;
2) 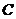 над над 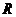 ; ;
3) 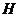 над над 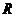 - поле кватернионов. - поле кватернионов.
Сейчас мы докажем, что других тел нет (т.е. все тела изоморфны какому-то из этих).
Лемма. Центр 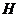 равен равен 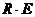 , т.е. все матрицы с одинаковыми вещественными числами по диагонали. , т.е. все матрицы с одинаковыми вещественными числами по диагонали.
Доказательство.
Пусть 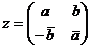 - элемент центра. Тогда - элемент центра. Тогда 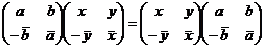 для любых для любых  и и  . Т.е. получаем систему . Т.е. получаем систему 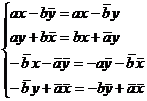 на элементы на элементы 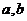 . Решая ее, получаем утверждение леммы. . Решая ее, получаем утверждение леммы. 
Определение. Пусть 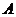 - ассоциативная алгебра с единицей над полем - ассоциативная алгебра с единицей над полем 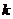 . Элемент . Элемент 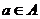 называется алгебраическим, если существует многочлен называется алгебраическим, если существует многочлен 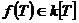 такой, что такой, что 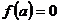 . Минимальным многочленом алгебраического элемента . Минимальным многочленом алгебраического элемента 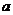 называется многочлен наименьшей степени со страшим коэффициентом называется многочлен наименьшей степени со страшим коэффициентом 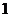 такой, что такой, что 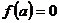 . .
Упражнение. Пусть 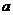 - алгебраический элемент из - алгебраический элемент из 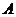 и и 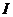 - все такие - все такие 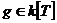 , что , что 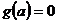 . Докажите, что . Докажите, что 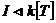 и и 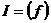 , где , где 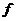 - минимальный многочлен элемента - минимальный многочлен элемента 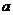 . .
Теорема. Пусть 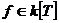 , тогда , тогда 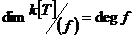 . .
Доказательство.
Возьмем 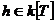 , , 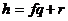 , где , где 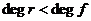 , следовательно, , следовательно, 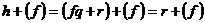 . Следовательно, . Следовательно, 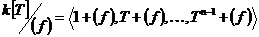 , где , где 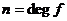 . Если . Если 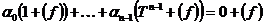 , то , то 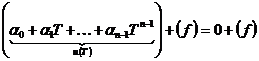 . Следовательно, . Следовательно, 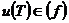 , т.е. , т.е. 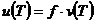 . Если . Если 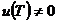 , то , то 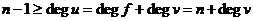 , что невозможно. Следовательно , что невозможно. Следовательно 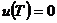 , следовательно, все , следовательно, все 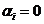 и элементы и элементы 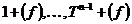 независимы. независимы. 
Теорема. 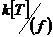 является полем тогда и только тогда, когда многочлен является полем тогда и только тогда, когда многочлен 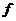 неприводим. неприводим.
Доказательство.
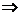 . Пусть . Пусть 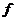 приводим, т.е. приводим, т.е. 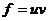 , где , где 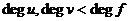 . Тогда . Тогда 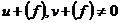 , и , и 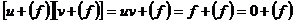 , т.е. есть делители нуля. Следовательно , т.е. есть делители нуля. Следовательно 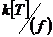 не поле. не поле.
 . Пусть . Пусть 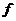 неприводим и неприводим и 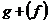 - ненулевой элемент. Тогда - ненулевой элемент. Тогда 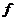 не делит не делит 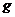 , т.е. , т.е. 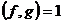 . Следовательно . Следовательно 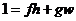 . Тогда . Тогда 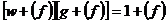 , т.е. каждый ненулевой элемент обратим. Следовательно , т.е. каждый ненулевой элемент обратим. Следовательно 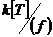 поле. поле. 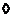
Определение. Пусть 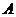 - алгебра и - алгебра и 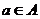 . Множество . Множество 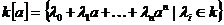 называется подалгеброй, порожденной элементом называется подалгеброй, порожденной элементом 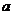 . .
Предложение. Пусть 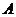 - область (ассоциативная алгебра с единицей и без делителей нуля) и - область (ассоциативная алгебра с единицей и без делителей нуля) и 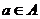 . Тогда минимальный многочлен . Тогда минимальный многочлен 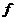 для для 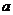 неприводим и неприводим и 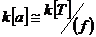 . В частности . В частности 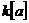 является полем. является полем.
Доказательство.
Пусть 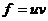 , где , где 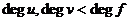 . Тогда . Тогда 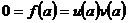 при при 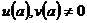 , но в , но в  нет делителей нуля. Получили противоречие, следовательно, нет делителей нуля. Получили противоречие, следовательно, 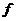 неприводим. неприводим.
Рассмотрим 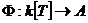 , такой что , такой что 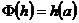 . Тогда . Тогда 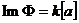 и и 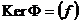 . По теореме о гомоморфизме получаем, что . По теореме о гомоморфизме получаем, что 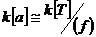 - поле. - поле. 
Предложение. Пусть 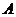 - конечномерное тело над - конечномерное тело над 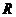 и и 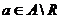 . Тогда . Тогда 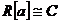 . .
Доказательство.
Пусть 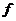 - минимальный многочлен из - минимальный многочлен из 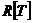 для для 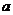 . Если . Если 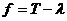 , , 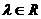 , то , то 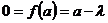 , следовательно , следовательно 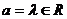 , противоречие. Следовательно , противоречие. Следовательно 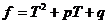 - неприводимый над - неприводимый над  . Тогда . Тогда 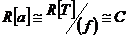 . (пусть . (пусть  - комплексный корень - комплексный корень 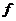 Тогда зададим Тогда зададим 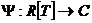 , т.ч. , т.ч. 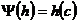 и воспользуемся т. о гомоморфизме). и воспользуемся т. о гомоморфизме). 
Теорема. Пусть 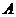 - поле, являющееся конечномерной алгеброй над - поле, являющееся конечномерной алгеброй над 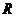 . Тогда . Тогда 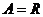 или или 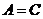 . .
Доказательство.
Пусть 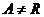 , тогда (по предыдущему предложению) , тогда (по предыдущему предложению) 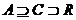 . Пусть . Пусть 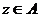 и и 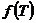 - минимальный многочлен для - минимальный многочлен для 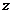 над над 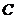 , тогда , тогда 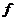 неприводим. Следовательно неприводим. Следовательно 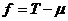 , где , где 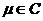 и и 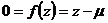 , т.е. , т.е. 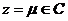 . Следовательно . Следовательно 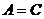 . . 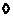
Теорема (Фробениуса). Пусть 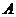 - конечномерное некоммутативное тело над - конечномерное некоммутативное тело над 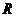 , тогда , тогда 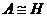 . .
Доказательство.
Т.к. 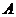 некоммутативно, то некоммутативно, то 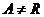 . Пусть . Пусть 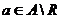 . Тогда . Тогда 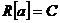 , следовательно , следовательно 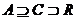 . . 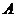 является левым векторным пространством над является левым векторным пространством над 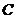 . Рассмотрим оператор . Рассмотрим оператор 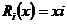 , это линейный оператор, т.к. , это линейный оператор, т.к. 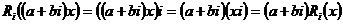 и и 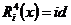 . Т.е. нам задано комплексное представление группы . Т.е. нам задано комплексное представление группы 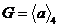 , , 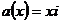 . Рассмотрим множества: . Рассмотрим множества:
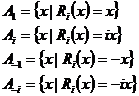 , тогда , тогда 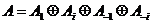 . .
Если 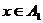 , то , то 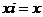 , т.е. , т.е. 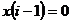 Т.к. в Т.к. в 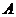 нет делителей нуля, то нет делителей нуля, то 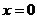 , т.е. , т.е. 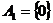 . Аналогично . Аналогично 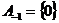 . Следовательно . Следовательно 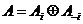 . .
Лемма 1. 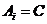 . .
Доказательство.
Пусть 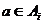 , тогда , тогда 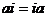 , следовательно , следовательно 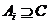 . Но . Но 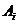 - подалгебра - подалгебра 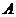 , являющееся конечномерным расширением , являющееся конечномерным расширением 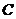 . А мы уже знаем, что в этом случае . А мы уже знаем, что в этом случае 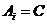 . . 
Лемма 2. Пусть 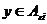 , , 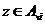 , где , где 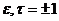 . Тогда . Тогда 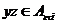 . .
Доказательство.
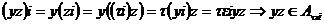 . . 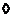
Лемма 3. Пусть 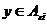 , тогда , тогда 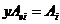 и и 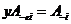 . .
Доказательство.
По предыдущей лемме 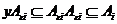 . Следовательно . Следовательно 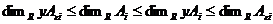 . Но с другой стороны . Но с другой стороны 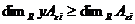 (т.к. в (т.к. в 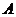 нет делителей нуля). Следовательно все эти неравенства обращаются в равенства и нет делителей нуля). Следовательно все эти неравенства обращаются в равенства и 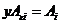 . Аналогично доказываем, что . Аналогично доказываем, что 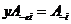 . . 
По лемме 1 имеем 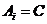 и и 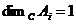 . Возьмем . Возьмем 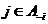 , тогда , тогда 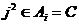 . Минимальный многочлен для . Минимальный многочлен для 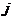 над над 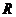 имеет степень 2. Следовательно имеет степень 2. Следовательно 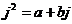 , где , где 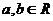 . Более того: . Более того: 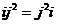 (т.к. (т.к. 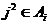 ) и ) и 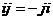 (т.к. (т.к. 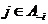 ). Следовательно, ). Следовательно, 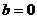 . Т.е. получаем, что . Т.е. получаем, что 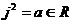 , причем , причем 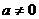 . .
Если 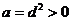 , то , то 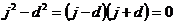 , т.е. , т.е. 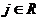 , что невозможно. , что невозможно.
Следовательно, 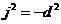 , где , где 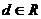 . Следовательно . Следовательно 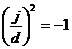 . Пусть . Пусть 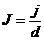 , тогда , тогда 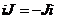 и и 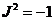 . Пусть . Пусть 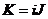 , тогда , тогда 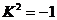 , , 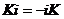 и и 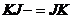 . .
В итоге мы получили, что 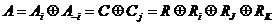 . Т.е. мы получили группу кватернионов . Т.е. мы получили группу кватернионов  (правила умножения совпадают). (правила умножения совпадают). 
Лекция 14 (3.12.2001)
Определение. Пусть 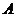 - область над полем - область над полем 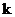 и и 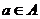 . Элемент . Элемент 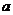 называется алгебраическим, если называется алгебраическим, если 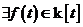 , такой что , такой что 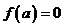 . Многочлен . Многочлен 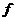 , наименьшей степени со старшим коэффициентом 1, такой что , наименьшей степени со старшим коэффициентом 1, такой что 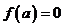 , называется минимальным аннулирующим многочленом для , называется минимальным аннулирующим многочленом для 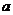 . .
Если 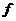 - минимальный многочлен для - минимальный многочлен для 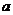 , то , то 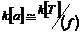 . .
Предложение. Если 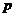 ненулевой над ненулевой над 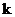 , тогда , тогда 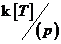 - поле. Элемент - поле. Элемент 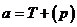 является корнем является корнем 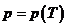 в поле в поле 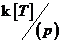 . .
Доказательство.
Пусть 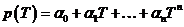 , , 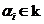 . Тогда . Тогда
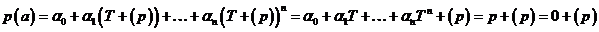 . . 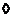
Следствие. Пусть 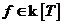 - произвольный. Тогда существует поле - произвольный. Тогда существует поле 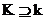 , в котором многочлен , в котором многочлен 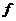 имеем корень. имеем корень.
Здесь 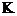 называется расширением поля называется расширением поля 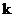 , записывается это как , записывается это как 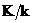 . .
Определение. Пусть 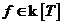 и и 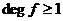 . Поле . Поле 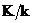 называется полем разложения для называется полем разложения для 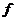 , если: , если:
1) над 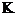 многочлен многочлен  разлагается на линейные множители; разлагается на линейные множители;
2) никакое промежуточное поле 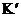 ( ( ) этим свойством не обладает. ) этим свойством не обладает.
Теорема. Пусть 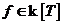 и и 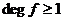 . Тогда: . Тогда:
1) поле разложения 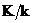 существует; существует;
2) если 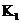 и и 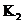 - поле разложения для - поле разложения для 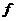 , то , то 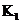 и и 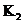 изоморфны как изоморфны как  -алгебры. -алгебры.
Доказательство.
1) Существование (доказательство по индукции).
Если 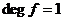 , то , то 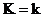 . .
Пусть теперь 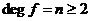 и для всех меньших степеней существование поля разложения уже доказано. Разложим и для всех меньших степеней существование поля разложения уже доказано. Разложим 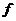 на неприводимые многочлены на неприводимые многочлены 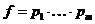 , , 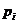 - неприводим. - неприводим. 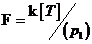 снова поле, и в нем многочлен снова поле, и в нем многочлен 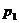 имеет корень имеет корень 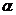 . Тогда в этом поле . Тогда в этом поле 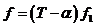 , где , где 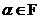 , , 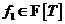 и и 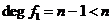 . По предположению индукции, существует . По предположению индукции, существует 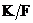 - поле разложения для - поле разложения для 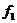 . Следовательно . Следовательно 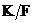 будет полем разложения для будет полем разложения для 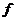 . .
2) Единственность (тоже по индукции).
Если 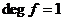 , то поле разложения единственно и равно , то поле разложения единственно и равно 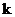 . .
Если 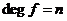 . Пусть . Пусть 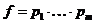 . Пусть . Пусть 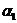 и и 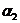 - корни - корни 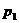 в полях в полях 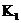 и и 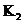 соответственно. Тогда соответственно. Тогда 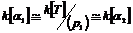 . Без ограничения общности можно считать, что . Без ограничения общности можно считать, что 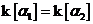 и и 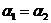 . Тогда . Тогда 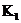 и и 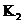 - поля разложения многочлена - поля разложения многочлена 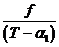 над над 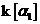 . По предположению индукции поля . По предположению индукции поля 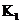 и и 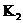 совпадают. совпадают. 
Вспомним из первого семестра, что, если 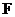 - поле, то - поле, то 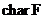 либо 0, либо простое число. Если характеристика равно нулю, то поле содержит в себе поле рациональных чисел. Если характеристика равна либо 0, либо простое число. Если характеристика равно нулю, то поле содержит в себе поле рациональных чисел. Если характеристика равна 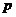 , то поле содержит в себе поле вычетов по модулю , то поле содержит в себе поле вычетов по модулю 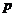 . .
Теорема. Пусть 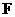 - конченое поле и - конченое поле и 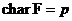 , тогда , тогда 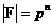 . .
Доказательство.
Т.к. 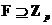 , то , то 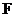 является векторным пространством над является векторным пространством над 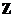 размерности размерности 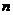 . Пусть . Пусть 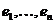 - базис в - базис в 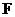 над над 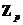 . Следовательно, . Следовательно, 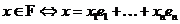 , где , где 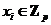 . Следовательно . Следовательно 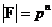 . . 
Предложение. Пусть 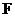 - поле характеристики - поле характеристики 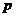 . Тогда . Тогда 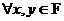 , , 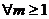 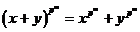 . .
Доказательство.
Докажем сначала для степени 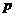 . По биному Ньютона . По биному Ньютона
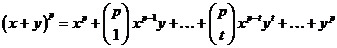 . .
Биноминальный коэффициент  равен равен 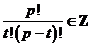 . Причем . Причем  , а , а 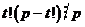 , следовательно, , следовательно, 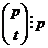 . Т.е. в поле . Т.е. в поле 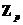 этот коэффициент равен нулю. Следовательно этот коэффициент равен нулю. Следовательно 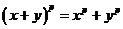 . .
В общем случае (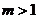 ) имеем: ) имеем:
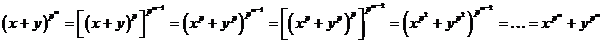 . . 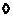
Теорема. Если 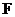 - поле из - поле из 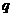 элементов и элементов и 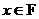 , то , то 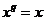 . .
Доказательство.
Пусть 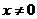 . Тогда . Тогда 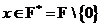 . Но . Но 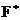 - группа по умножению порядка - группа по умножению порядка 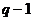 , следовательно, , следовательно, 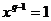 , следовательно, , следовательно, 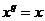 . .
Если 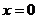 , то утверждение очевидно. , то утверждение очевидно. 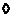
Теорема. Пусть 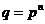 , где , где 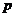 - просто, тогда существует (и оно единственно) поле - просто, тогда существует (и оно единственно) поле 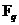 и и 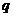 элементов. элементов.
Доказательство.
Рассмотрим поле  и многочлен и многочлен 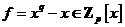 . Пусть . Пусть 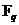 - поле разложения для - поле разложения для 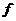 . Пусть . Пусть 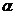 и и 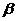 - корни - корни 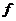 , тогда , тогда 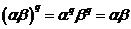 , т.е. , т.е. 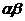 - тоже корень - тоже корень 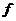 . По доказанному выше предложению . По доказанному выше предложению 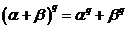 , т.е. , т.е. 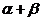 - тоже корень - тоже корень 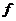 . Аналогично проверяем, что . Аналогично проверяем, что 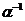 и и 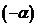 тоже будут корнями тоже будут корнями 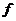 . .
Если 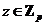 , то , то 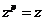 , следовательно, и , следовательно, и 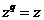 . Все корни . Все корни 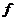 образуют подполе. Следовательно образуют подполе. Следовательно 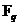 совпадает с множеством всех корней многочлена совпадает с множеством всех корней многочлена 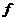 . У многочлена . У многочлена 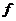 нет кратных корней, т.к. нет кратных корней, т.к. 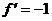 и и 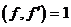 - взаимопросты. Следовательно - взаимопросты. Следовательно 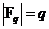 . Единственность поля следует из единственности поля разложения для многочлена. . Единственность поля следует из единственности поля разложения для многочлена.  . .
Теорема. Пусть 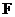 - поле и - поле и 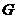 - конечная подгруппа в - конечная подгруппа в 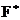 . Тогда . Тогда 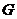 - циклическая. - циклическая.
Доказательство.
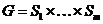 , где , где  - силовская - силовская  - подгруппа. Нам достаточно доказать, что каждая - подгруппа. Нам достаточно доказать, что каждая  циклическая. циклическая.  , где , где 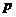 - простое число. Пусть элемент - простое число. Пусть элемент 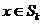 имеет максимальный порядок ( имеет максимальный порядок (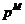 ). Тогда ). Тогда 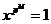 или или 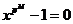 . Рассмотрим многочлен . Рассмотрим многочлен 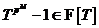 . Любой элемент . Любой элемент 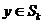 имеет порядок имеет порядок 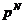 , где , где 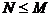 . Следовательно, . Следовательно, 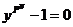 и и 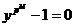 . Т.е. все элементы . Т.е. все элементы 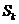 являются корнями многочлена являются корнями многочлена 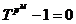 . Но и всего . Но и всего 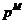 , следовательно, , следовательно, 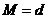 и порядок элемента и порядок элемента 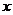 совпадает с порядком всей группы. Следовательно, группа совпадает с порядком всей группы. Следовательно, группа  циклическая, порожденная элементом циклическая, порожденная элементом 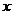 . Следовательно и вся группа . Следовательно и вся группа 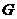 циклическая. циклическая. 
Следствие. 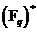 - циклическая группа. - циклическая группа.
Следствие. Пусть 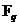 - поле и - поле и 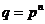 . Тогда существует многочлен . Тогда существует многочлен 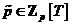 степени степени 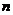 такой, что такой, что 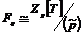 . .
Доказательство.
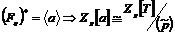 , где , где 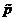 - минимальный аннулирующий многочлен. - минимальный аннулирующий многочлен. 
Теорема. Группа автоморфизмов 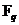 , где , где 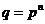 является циклической группой порядка является циклической группой порядка 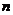 . .
Доказательство.
Пусть 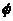 - автоморфизм - автоморфизм 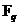 , тогда , тогда 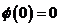 , , 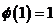 , , 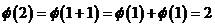 , т.е. , т.е. 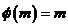 , если , если 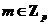 . Тогда . Тогда 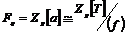 , где , где 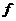 - минимальный аннулирующий многочлен для - минимальный аннулирующий многочлен для 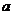 , , 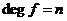 . Пусть . Пусть 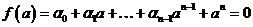 , тогда , тогда 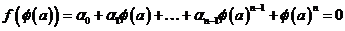 . Для . Для 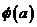 имеется не более имеется не более 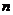 значений. Следовательно, существует не более значений. Следовательно, существует не более 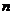 автоморфизмов автоморфизмов 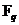 . .
Укажем автоморфизм порядка 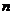 . . 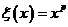 , тогда , тогда 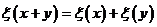 и и 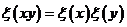 . Тогда . Тогда 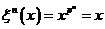 , т.е. , т.е. 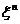 - тождественный автоморфизм. Если порядок - тождественный автоморфизм. Если порядок 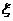 равен равен 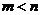 , то , то 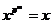 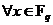 и тогда в поле и тогда в поле 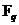 будет всего будет всего 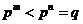 элементов. Следовательно, порядок элементов. Следовательно, порядок 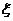 равен равен 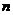 и и 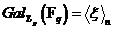 . . 
|

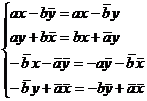 на элементы
на элементы 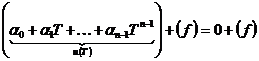 . Следовательно,
. Следовательно, 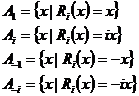 , тогда
, тогда