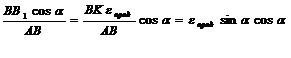Деформации при растяжении-сжатии и закон Гука

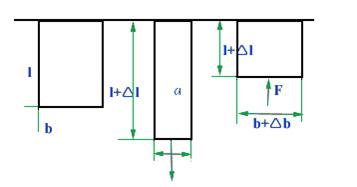
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются. При сжатии наоборот.

Рис.2.3

 (2)-относительное удлинение или линейные деформации.

Для многих конструкционных материалов при нагружении до определенных пределов опыты показывают линейную зависимость линейных деформаций от нормальных напряжений.

   (3)- закон Гука.

Е- модуль продольной упругости или упругости первого рода.

Значения модуля упругости для некоторых материалов (в МПа):

• сталь- 2.105-2.2.105;
• титан- 1.1.105;
• алюминий- 0.675. 105;
• медь- 1.105;
• стеклопластик- 0.18.105-0.4.105;

После подстановки (1) и (2) в (3):

=            (4)

Между продольной ε и поперечным εtдеформациями существует следующая экспериментальная зависимость:

 (5)

 - коэффициент поперечной деформации (коэффициент Пуассона).

Если рассматривать произвольно ориентированный прямоугольник АВСД, то стороны его удлиняются, а сам прямоугольник под действием касательных напряжений переносится и превращается в параллелограмм. Углы А и С уменьшатся, а В и Д увеличатся.

Изменение прямого угла называется угловой деформацией или углом сдвига.

Найдем угла поворота отрезков АВ и АД..

Угол поворота под действиям продольного удлинения:

=

Угол поворота под действием поперечного сужения:

Для определения угла поворота АД вместо α нужно использовать

Угловая деформация или угол сдвига:

Или введя модуль упругости G или модуль упругости второго рода:

 (1)

  (2)

Определение удельной теплоемкости твердых тел методом адиабатического калориметра

Измерение коэффициента диффузии паров легко испаряющейся жидкости в воздухе

Определение длины свободного пробега и эффективного диаметра молекул газа по коэффициенту внутреннего трения

Получение низких давлений

Термопарный манометр - вакууметр

Вернуться в оглавление: Физика