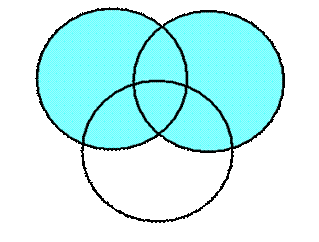
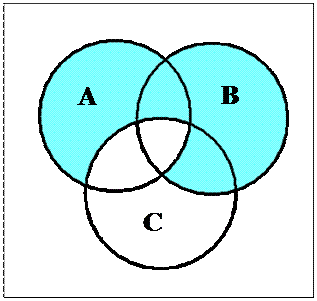
Пример 1. Изобразить следующие множество с помощью диаграммы Венна (АUВ)\(С∩А):
|
 | |||||
| |||||
 |
|
 | |||||
 | |||||
 |
3) (АUВ)\(С∩А):
 |
Пример 2. Даны множества А={2, 3, 5, 8, 13, 15}, В={1, 3, 4, 8,
16}, С={12, 13, 15, 16}, D={0, 1, 20}. Найти А 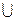 В, С
В, С 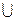 D, В∩С, А∩D,
D, В∩С, А∩D,
А\С, D\В, А 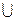 В
В 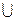 С, А∩В∩С, В
С, А∩В∩С, В 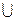 D∩С, А∩С\D.
D∩С, А∩С\D.
Решение: Будем пользоваться определениями соответствующих операций и учтем, что сначала должна выполняться операция пересечения множеств, а затем уже объединение или разность. Получим А 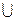 В={1, 2, 3, 4, 5, 8, 13, 15, 16}, С
В={1, 2, 3, 4, 5, 8, 13, 15, 16}, С 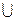 D={0, 1, 12, 13, 15, 16, 20}, В∩С={16}, А∩D=∅, А\С={2, 3, 5, 8}, D\В={0, 20}, А
D={0, 1, 12, 13, 15, 16, 20}, В∩С={16}, А∩D=∅, А\С={2, 3, 5, 8}, D\В={0, 20}, А 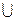 В
В 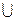 С={1, 2, 3,4, 5, 8, 12, 13, 15, 16}, А∩В∩С=∅, В
С={1, 2, 3,4, 5, 8, 12, 13, 15, 16}, А∩В∩С=∅, В 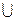 D∩С={1, 3, 4, 8, 16},А∩С\D={13, 15}. ♦
D∩С={1, 3, 4, 8, 16},А∩С\D={13, 15}. ♦
Пример 3. Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти получили 180 человек, а выдержали этот экзамен 210 абитуриентов. Сколько человек получили оценки 3 и 4?
Решение: Пусть А – множество абитуриентов, выдержавших экзамен, В – множество абитуриентов, получивших оценку ниже 5, по условию m (A)=210, m (В)=180, m (A 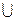 B)=250. Абитуриенты, получившие оценки 3 и 4, образуют множество А∩В. Из формулы (2) находим m (A∩B) = m (A) + m (В) - m (A
B)=250. Абитуриенты, получившие оценки 3 и 4, образуют множество А∩В. Из формулы (2) находим m (A∩B) = m (A) + m (В) - m (A 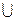 B) = 210 + 180 – 250 = 140.♦
B) = 210 + 180 – 250 = 140.♦
|
|
|
Пример 4. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на коньках и на лыжах?
Решение: Множество учеников школы будем считать основным множеством U, А и В – соответственно множества учеников, умеющих кататься на лыжах и на коньках. Учащиеся, не умеющие кататься ни на лыжах, ни на коньках, составляют множество А’∩В’.
m (А∩B) = m (А) + m (В) - m (А 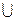 B) = 862. ♦
B) = 862. ♦
По условию m (А’∩B’) = 60, а т.к. по формуле (3) А’∩B’=(А 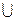 В)’, то и m (А
В)’, то и m (А 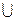 B)’= 60. Отсюда m (А
B)’= 60. Отсюда m (А 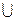 B) = m (U) - m (А
B) = m (U) - m (А 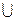 B)’=1340. Зная m (А) и m (В), по формуле (2) находим.
B)’=1340. Зная m (А) и m (В), по формуле (2) находим.
Декартово произведение множеств. Соответствия. Бинарные отношения и их свойства. Отображения.
Рассмотрим следующую реальную ситуацию. Фабрика верхнего трикотажа изготовляет мужские пуловеры, женские костюмы, кофты и платья следующих расцветок: бордо, синяя, голубая, зеленая, коричневая, серая. Обозначим через А множество видов изделий: А={мужской пуловер, женский костюм, кофта, платье}, через В – множество предлагаемых расцветок: В={бордо, синяя, голубая, зеленая, коричневая, серая}. Посмотрим, какие изделия можно получить, учитывая возможные для них расцветки. Для этого составим список всех пар из элементов множества А и элементов множества В таким образом, что сначала будем записывать элемент множества А, затем элемент множества В. получим множество С упорядоченных пар элементов множеств А и В. Возможные изделия можно перечислить с помощью таблицы. Итак, мы имеем дело с особым множеством, составленным из элементов двух данных множеств. Такое произведение называется декартовым произведением двух множеств.
|
|
|
| В А | мужской пуловер | женский костюм | Кофта | Платье |
| Бордо | пуловер-бордо | костюм женский –бордо | кофта–бордо | платье –бордо |
| Синяя | пуловер - синий | костюм женский – синий | кофта - синяя | платье - синее |
| Голубая | пуловер - голубой | костюм женский – голубой | кофта - голубая | платье - голубое |
| Зеленая | пуловер - зеленый | костюм женский – зеленый | кофта – зеленая | платье - зеленое |
| Коричневая | пуловер - коричневый | костюм женский – коричневый | кофта - коричневая | платье –коричневое |
| Серая | пуловер - серый | костюм женский – серый | кофта - серая | платье - серое |
Опр. 1 Декартовым ( или прямым) произведением множества А на множество В называется множество всех упорядоченных пар, в которых первая компонента – элемент множества А, а вторая – элемент множества В. Обозначают А×В.
Таким образом, А×В={(x, y) | х  А и y
А и y  В}.
В}.
Может случиться, что множества А и В окажутся одинаковыми. Рассмотрим следующий пример. Фабрика «Авторучка» изготовляет отдельно корпус и колпачок авторучек следующих цветов: белый, красный, зеленый, оранжевый.
Обозначим через А – множество цветов корпуса ручки, через В – множество цветов колпачка. Тогда получим: А=В={белый, красный, зеленый, оранжевый}. Можно составить список возможных колоритов для авторучки: цвет корпуса и цвет колпачка.
Объединяя всеми возможными способами цвет из А с цветом из В=А, получим элементы прямого произведения множества А «самого на себя», которое называется прямым или декартовым квадратом и обозначается: А×А=А2.
Из этого примера видно, что каждая пара прямого произведения должна быть упорядочена: красная ручка с белым колпачком отличается от белой ручки с красным колпачком.
Для описания прямого произведения множеств бывает удобно использовать «геометрический язык». При этом элементы множества А×В называются точками. Например, если z=(x,y), то х  А называется абсциссой, а y
А называется абсциссой, а y  В – ординатой точки z. В связи с этим заметим, что множество точек плоскости по существу являются элементами прямого квадрата R × R = R 2 множества R действительных чисел.
В – ординатой точки z. В связи с этим заметим, что множество точек плоскости по существу являются элементами прямого квадрата R × R = R 2 множества R действительных чисел.
На рис.1 точками показаны элементы декартова произведения множеств А={1, 2, 3} и В={4, 5, 6, 7}. Отсюда легко видеть способ нахождения общего числа элементов в декартовом произведении двух множеств: если m (А)= n, m (B)= k, то m (А×В)=n*k (5).

Рис.1.
Пример 1. Применим формулу (5) для подсчета количества двухзначных чисел. Двухзначное число можно принять за упорядоченную пару, где на первом месте может стоять цифра из множества А={1, 2, 3, 4, 5, 6, 7, 8, 9}, а на втором – из множества В={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. за элемент прямого произведения этих множеств, тогда получаем: m (А)=9, m (B)=10, то m (А×В)=9·10=90. Итак, всего имеется 90 различных двухзначных чисел. ♦
Перейдем к знакомству с другим новым понятием. Рассмотрим два множества: первое (А), состоящее из 11 учащихся, второе (В), состоящее из 9 городов. Чтобы получить прямое произведение этих множеств, надо составить все пары: (ученик – город). Из множества всех таких пар мы выберем лишь такие, которые «связывают» каждого ученика с тем городом, где он бывал. Очевидно, что «список» таких пар (ученик – известный город) будет являться подмножеством Ω декартова произведения. Такой «список» удобно заменить таблицей, где можно указать все города, в которых побывал каждый ученик:
| Москва | Тула | Одесса | Тамбов | Воронеж | Липецк | Елец | Задонск | Лебедянь | |
| Петя | × | × | × | × | |||||
| Вася | × | × | × | ||||||
| Коля | × | × | × | ||||||
| Саша | × | × | × | ||||||
| Лена | × | × | × | ||||||
| Таня | × | × | × | ||||||
| Ирина | × | × | |||||||
| Вера | × | × | |||||||
| Андрей | × | × | × | ||||||
| Витя | × | × | × | × | |||||
| Катя | × | × |
Можно сказать, что данная таблица задает определенное соотношение между элементами множеств А и В.
|
|
|
Опр.2 Будем говорить, что между элементами двух множеств А и В установлено соответствие ρ, если в их произведении А×В выделено некоторое подмножество Ω. Если пара (a,b)  Ω
Ω 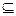 Α×Β, это означает по определению, что элементы a и b множеств А и В находятся в отношении ρ (пишется aρb).
Α×Β, это означает по определению, что элементы a и b множеств А и В находятся в отношении ρ (пишется aρb).
Еще один пример соответствия: Пусть даны множества А – студентов и В – множество групп. Утверждение “студент a учится в группе b ” задает соответствие между множеством студентов и множеством групп. Здесь а пробегает множество значений А, b – множество значений В. Такое соотношение называется бинарным соответствием, т.е. соответствием между двумя множествами А и В.
Бинарные соответствия можно задавать таблицами (например, расписание занятий) или ориентированными графами.
| Пн. | Вт. | Ср. | |
| Педагогика | |||
| Математика | |||
| Физкультура |
Рис. 2. 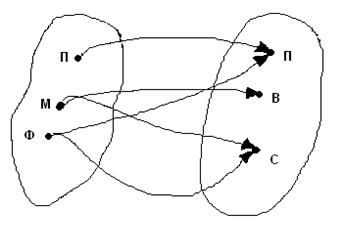
Если соответствие ρ задано между элементами одного и того же множества, то говорят, что между элементами этого множества задано отношение ρ. Итак, задать на множестве А 2-хместное (бинарное) отношение означает выделить в прямом квадрате А2 этого множества некоторое подмножество Ω.
Опр.3 Бинарным отношением, заданным на множестве А называется всякое подмножество декартова произведения А×А.
Местность отношения показывает сколько объектов могут разом находиться в данном отношении. Чаще всего рассматриваются бинарные (двухместные) или тернарные (трехместные) отношения.
|
|
|
Таким образом, бинарные соответствия между X и X называются бинарными отношениями на множестве X, т.е. соответствиями между элементами одного и того же множества (или равных множеств). Например, отношения: “2>1”, “3=3”, “человек х старше человека y” и др.
Пример 2. Возьмем в качестве элементов множества А случайную группу людей (например, едущих в одном поезде). И выберем бинарное отношение ρ на этом множестве следующим образом: два человека из А будут находиться в данном отношении, если они родились в одном и том же месяце (под одним знаком зодиака; имеют одинаковые имена и пр.). И еще элемент а1 из А будет находиться в отношении δ с элементом а2 из того же множества, если, допустим, первый человек выше ростом, чем второй (старше, тяжелее и пр.).
Из этих примеров можно заметить, что если Таня родилась в том же месяце, что и Петя, то же самое можно сказать и о Пете: Петя родился в том же месяце, что и Таня. С учетом введенных обозначений можно записать: если ТаняρПетя, то ПетяρТаня. Иначе дело обстоит с другим отношением δ: если Таня ростом выше Пети, то неверно, что и Петя ростом выше Тани.
Таким образом, различные отношения могут иметь и различные свойства. Рассмотрим основные из них.
Опр.4 Бинарное отношение (БО) ρ, заданное на множестве А, называется рефлексивным, если любой элемент этого множества находится в данном отношении с самим собой, т.е. 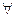 а
а  А: аρа.
А: аρа.
Опр.5 БО ρ называется симметричным, если из того, что пара (a,b) находится в отношении ρ, следует, что и симметричная ей пара (b,a) тоже находится в этом отношении, т.е 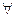 a,b
a,b  A: aρb
A: aρb 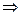 bρa.
bρa.
Опр.6 БО называется антисимметричным, если 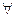 a,b
a,b  A: aρb
A: aρb 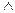 bρa
bρa 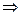 a=b.
a=b.
Опр.7 БО называется транзитивным, если 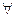 a,b,c
a,b,c  A:
A:
aρb 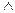 bρc
bρc 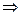 aρc.
aρc.
Примерами рефлексивного и транзитивного отношения является отношение равенства, не симметричного – отношения «больше» или «меньше» на множестве действительных чисел.
БИНАРНЫЕ ОТНОШЕНИЯ (ОПРЕДЕЛЕНИЯ)
| БО ρ, заданное на множестве А, является: | Если выполняется следующее условие: |
| Рефлексивным Симметричным Антисимметричным Транзитивным | 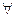 а а  А aρa А aρa
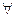 a,b a,b  A aρb A aρb 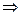 bρa bρa
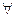 a,b a,b  A aρb A aρb 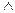 bρa bρa 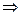 a=b a=b
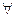 a,b,c a,b,c  A aρb A aρb 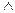 bρc bρc 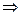 aρc aρc
|
Опр.8 Бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности (или просто эквивалентностью).
Бинарное отношение ρ можно задать перечислением всех пар из А×А, принадлежащих отношению, указанием характеристического свойства, которым обладают все элементы отношения, а также с помощью так называемого ориентированного графа. Для этого элементы множества А изображают в виде точек и вводят соглашение: если x ρ y, то от точки x проводят стрелку к точке y. Если x ρ х, то начало и конец стрелки совпадают, такую стрелку называют петлей. Выполнив указанные построения, получим фигуру – ориентированный граф. Точки, соединенные стрелками, называются вершинами графа, а сами стрелки – ребрами графа.
Пример 3. Пусть на множестве М={2,3,4,5,6} задано отношение ρ -кратности элементов, т.е. x ρ y, если x M y (x делится на y без остатка). Построить ориентированный граф данного бинарного отношения.
Решение: Заметим, что по графу (рис. 13) наглядно можно судить о свойствах данного отношения: замкнутые на каждом элементе круглые стрелочки – признак рефлексивности отношения; единственная стрелка (а не с обеих сторон) у линии, соединяющей один элемент данного множества с другим, говорит о том, что отношение не является симметричным; отсутствие хотя бы у одной пары элементов соединяющих их стрелок указывает на то, что отношение не антисимметрично и т.д. ♦
Рассмотрим еще один частный случай общего понятия “соответствие” – отображение множеств.
Рассмотрим два множества X и Y.
Опр 9 Если каждому элементу x  X поставлен в соответствие единственный элемент y
X поставлен в соответствие единственный элемент y  Y, то такое соответствие называется отображением множества Х в множество Y. Т.е., каждому элементу х соответствует только один элемент y Обозначается отображение множеств так: f: X→Y, здесь f – символ самого отображения.
Y, то такое соответствие называется отображением множества Х в множество Y. Т.е., каждому элементу х соответствует только один элемент y Обозначается отображение множеств так: f: X→Y, здесь f – символ самого отображения.
Пример 4 Пусть Х – множество студентов в аудитории, Y – множество столов в этой аудитории. Соответствие “студент х сидит за столом y ” задает отображение множества Х в множество Y. Это очевидно, так как все студенты сидят за столом, иногда по двое, по трое и т.д., но есть и пустые столы. При таком отображении множества Х в множество Y, элемент y  Y называется образом элемента x
Y называется образом элемента x  X, а элемент x
X, а элемент x  X называется прообразом элемента y
X называется прообразом элемента y  Y.
Y.
Опр.10 Если при отображении f каждому элементу x  X поставлен в соответствие один элемент y
X поставлен в соответствие один элемент y  Y, при этом соответствии каждому элементу y
Y, при этом соответствии каждому элементу y  Y соответствует единственный элемент x
Y соответствует единственный элемент x  X, то такое отображениеназывается взаимно-однозначным.
X, то такое отображениеназывается взаимно-однозначным.
Пример 5 Пусть Х – множество студентов, Y – множество зачетных книжек. Соответствие “студенту х принадлежит зачетная книжка y ” задает взаимно-однозначное отображение между множествами Х и Y. Это очевидно, так как все студенты имеют зачетные книжки, причем каждый только одну и каждая зачетная книжка принадлежит своему студенту.
 2015-05-22
2015-05-22 10085
10085