Теорема Бернулли. Значение закона больших чисел.
Теорема: Если в-ть р наст-ия соб А в n-независимых испытаниях постоянна, то при неограниченном увеличении числа n относительная частота k/n появления события А в n испытаниях ст-ся по в-ти к вер-ти р, т.е. 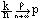
Док-во: как и в биномиальном з-не распределения число к наст-я соб. А в n испытаниях может быть представлено как к= 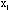 ,
, 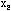 ,…,
,…, 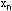 ,, где
,, где 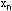 - индикатор наступления соб. А в i-ом испытании
- индикатор наступления соб. А в i-ом испытании 
Было д-но, М(х  )=p, а D(х
)=p, а D(х  )=pq=c, тогда, подставляя в (6)
)=pq=c, тогда, подставляя в (6) 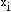 и D(х
и D(х  ), получим
), получим 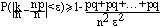 (8)Неравенство Бернулли
(8)Неравенство Бернулли
Значение з-на больших чисел:
1 в физике-пос-во давления газа
2 в статистике-основа выбора метода
3 в страховании-основанно на устойчивых таблицах смертности
Вопрос 31 Понятие о центральной предельной теореме и ее следствиях.
Суть центральной предельной теоремы (ЦПТ) в след.:
Если с.в х представляет собой сумму оч. большого числа взаимно независимых случ. в-н, влияние каждой из которых на всю сумму ничтожно мало, то х имеет расп-е, близкое к нормальному.Центральная предельная теорема (ЦПТ) (в формулировке Ляпунова А.М. для одинаково распределенных СВ). Если попарно независимые СВ X1, X2,..., Xn,... имеют одинаковый закон распределения с конечными числовыми характеристиками M[Xi] = m и D[Xi] = s2, то при n ® ¥ закон распределения СВ 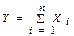 неограниченно приближается к нормальному закону N(n×m,
неограниченно приближается к нормальному закону N(n×m, 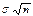 ).
).
Следствие. Если в условии теоремы СВ 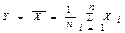 , то при n ® ¥ закон распределения СВ Y неограниченно приближается к нормальному закону N(m, s/
, то при n ® ¥ закон распределения СВ Y неограниченно приближается к нормальному закону N(m, s/ 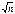 ).
).
(Не до конца,?????)
Вопрос 32 Локальная и интегральная теоремы Лапласа как следствие теоремы Ляпунова.
Теорема Муавра-Лапласа. Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ и фиксированном значении вероятности “успеха” в одном испытании p закон распределения СВ K неограниченно приближается к нормальному закону N(n×p, 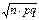 ).
).
Пусть СВ Xi подчиняется закону распределения Бернулли, следовательно M[Xi] = p и D[Xi] = s2 = p×q. Так как согласно ЦПТ при n ® ¥ и фиксированном значении p закон распределения СВ 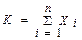 неограниченно приближается к нормальному закону N(n× p,
неограниченно приближается к нормальному закону N(n× p, 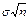 ), что и требовалось показать. 4
), что и требовалось показать. 4
Следствие. Если в условии теоремы вместо СВ К рассмотреть СВ К/n - частоту “успехов” в n испытаниях по схеме Бернулли, то ее закон распределения при n ® ¥ и фиксированном значении p неограниченно приближается к нормальному закону N(p, 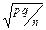 ).
).
Замечание. Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Законом распределения такой СВ является биноминальный закон. Тогда при n ® ¥ биноминальный закон имеет два предельных распределения:
распределение Пуассона (при n ® ¥ и l = n×p = const);
распределение Гаусса N(n×p, 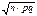 ) (при n ® ¥ и p = const).
) (при n ® ¥ и p = const).
Вопрос 32 Теорема Ляпунова
Если независимые СВ X1, X2…Xn имеют мат ожидания A1, A2…An, дисперсии δ1,δ2,δn и абсолютные центр моменты 3го порядка С1,С2,Сn, если выполняется условие Ляпунова
limn→∞(C1+C2+…Cn)/(δ1+δ2+…+δn)3/2=0, тоX1+X2+Xn при n→∞ распределена по нормальному закону с параметрами a=a1+a2+an, δ=δ1+δ2+δn. Заменяя практическое распределение нормальным законом мы совершаем погрешность, но на практике если n>=30, погрешность незначительна.
Вопрос 33 Предмет и задачи мат статистики, ген и выборочная совокупности, способ отбора.
Мат стат-раздел математики, изучающий методы отбора, систематизации и обработки результатов наблюдений, массовых случ явлений с целью выяснения существующих закономерностей. Задачи:1-указание способов сбора и группировки стат сведений (описательная статистика) 2-разработка методов анализа стат данных а) оценка вероятности события б)функции распределения в) зависимость случ величины от других величин г) проверка стат гипотез. Ген сов-ть – сов-ть объектов, все элементы кот подлежат изучению; м.б. конечной/бесконечной. Выборочная сов-ть часть объектов ген сов-ти используемая для исследования. Способы отбора: 1)простой случайный бесповторный, когда кажд элемент, случайно отобранный исследователем, не возвращается в ген сов-ть 2)простой случайный повторный отбор, когда элемнт возвращается в ген сов-ть
Вопрос 34 Построение дискретного вариационного ряда. Эмпирическая ф-ия распределения.
Дан ряд чисел. Частота варианты-(Xi) число mi, показывающее сколько раз эта варианта встречается в выборке. Частость(относительная частота) доля варианты W=mi/n. Полигон частот-ломаная линия, соединяющая точки плоскости с координатами(Xi, Mi). Кумулянта- ломаная, соединяющая с координатами (Xi, Mxi). Эмпирическая ф-ия распределения F*(x)=mi/n=Wx. Св-ва F*:1. 0<=F*<=1; 2. неубывающая; если x1-наименьшая варианта, а Xk-наибольшая варианта, то F*(x)=0 при x<=x1 и F*(x)=1 при x>xk
Вопрос 35 Построение интервального вариационного ряда. Гистограмма частот.
В общем случае справедлива теорема: M(Dв)=((n-1)/n)Dr. Вводится понятие исправленной выборочной дисперсии S²=(n/(n-1))Dв=(∑(xi-x)²mi)/(n-1). Если произведена выборка небольшого объема, то точечная оценка непригодна, тогда поступают так: по сделанной выборке находим точечную оценку Ô→выборочное неизвестного параметра Ô ген сов-ти; по опр правилам вычисляем такое число ∆>0, чтобы интервал с данной вероятностью γ (или P) включал в себя неизвестный параметр Ô, т.е. чтобы была справедлива формула доверительной вероятности (1) P(Ô-∆<Ô<Ô+∆)=γ(гамма, доверит. вероятность). ∆-точность оценки, (Ô-∆;Ô+∆)-доверительный интервал.
Вопрос 36 Средняя арифметическая и ее свойства. Устойчивость выборочных средних
Пусть дан дискретный вариационный ряд
| Xi | x1 | x2 | xi | xn |
| Mi | m1 | m2 | mi | mn |
Средняя арифметическая ряда называется число х = (Sxi.mi)/(Smi)
Существует ряд свойств средней арифметической, облегчающих ручные вычисления (метод произведения)
Вопрос 37 Дисперсия вариационного ряда и ее св-ва. Исправленная выборочная дисперсия.
Диперсией вариационного ряда называется число D=S((xi-x)^2)/n, xi-с-на интервала, если ряд интервальный
Вопрос 39 Доверительный интервал Jg(s) = (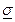 ,
, 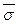 )
)
Постановка задачи. Пусть СВ X ~ N(m, s), где m и s - неизвестные параметры. По выборке объема n требуется построить ДИ для параметра s с уровнем доверия g.
Для этого воспользуемся тем, что СВ 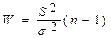 ~ c2n-1, где
~ c2n-1, где 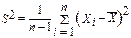 - точечная оценка дисперсии D[X]. По таблицам c2 - распределения найдем квантили уровня (1-g)/2 и (g+1)/2 распределения Пирсона с (n-1) степенями свободы x (1-g)/2 и x (g+1)/2, для которых справедливо:
- точечная оценка дисперсии D[X]. По таблицам c2 - распределения найдем квантили уровня (1-g)/2 и (g+1)/2 распределения Пирсона с (n-1) степенями свободы x (1-g)/2 и x (g+1)/2, для которых справедливо:
P{x (1-g)/2 < W < x (g+1)/2} = P{W < x (g+1)/2} - P{W < x (1-g)/2} = (g + 1)/2 - (1 - g)/2 = g.
Проводя элементарные преобразования, получаем:
P{(n-1)S2/x (g+1)/2 < s2 < (n-1)S2/x (1-g)/2} = g и P{[(n-1)S2/x (g+1)/2]1/2 < s < [(n-1)S2/x (1-g)/2]1/2} = g,
где S2 - точечная оценка дисперсии D[X]. Тем самым получены ДИ для параметров s2 и s:
Jg(s2) = ((n-1)s2/x (g+1)/2, (n-1)s2/x (1-g)/2) и Jg(s) = ([(n-1)s2/x (g+1)/2]1/2, [(n-1)s2/x (1-g)/2]1/2),
где x (1-g)/2 и x (g+1)/2 - квантили уровня (1-g)/2 и (g+1)/2 распределения Пирсона с (n-1) степенями свободы;
s2 - выборочное значение дисперсии D[X].
Пример. Пусть измеряемая величина X ~ N(m, s) - давление газа. По четырем испытаниям установлены: выборочное среднее 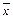 = 120 МПа и выборочное значение дисперсии s2 = 4 (МПа)2. Требуется определить ДИ для sX с уровнем значимости a = 0,1.
= 120 МПа и выборочное значение дисперсии s2 = 4 (МПа)2. Требуется определить ДИ для sX с уровнем значимости a = 0,1.
Решение. Сначала определим квантили уровня 0,05 и 0,95 распределения Пирсона с 3 степенями свободы: x0,05 = c23; 0,95 = 0,35 и x0,95 = c23; 0,05 = 7,8. Следовательно J0,9(sX) = (1,24; 5,8) МПа.
Вопрос 41 Основные понятия стат проверки гипотез. Гипотезы H0 и H1, критерии проверки, ошибки первого и второго рода, критическая область, мощность критерия.
Стат гипотеза – любое предположение о параметрах и св-вах ген распределения. Подлежащая проверке гипотеза – основная/нулевая гипотеза H0. Гипотеза, противопоставленная Н0, называется конкурирующей/альтернативной Н1. Критерий проверки-правило, по кот решают отклонять или не отклонять проверяемую гипотезу.Он реализуется с помощью случ вел (статистики) Ô, определенной на выбранном пространстве.Все множество критериев Ô разбивают на 2: 1)критическая область W0 2)допустимая область S. Критическая область-подмножество W0 возможных значений критерия, при кот гипотезу отклоняют. Виды: левосторонняя, правосторонняя, двусторонняя. W0={Ô:P(Ô€W0=α}. Если по результатам выборки оказывается, полученное значение критерия Ôнабл€W0, то гипотезу отклоняют.
Вопрос 42 Проверка гипотезы о равенстве мат ожиданий 2ух нормально распределенных ген сов при известной дисперсии.
Н0: M(X)=M(Y) при
Н1: M(X)≠M(Y); M(X)>M(Y); M(X)<M(Y)
Для проверки данной гипотезы используется критерий Z= (X-Y)/√(D(X)/n1+D(Y)/n2), где n1-выборка из x, n2-выборка из у.
Вопрос 44 Распределение Пирсона (или “хи”-квадрат распределение
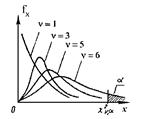
Пусть СВ 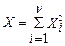 , где Xi ~ N(0, 1) - независимые нормированные нормально распределенные СВ. Тогда X подчиняется распределению “хи”-квадрат с n степенями свободы: X ~ cn2. С ростом n “хи”-квадрат распределение приближается к нормальному с параметрами mX = n и sX =
, где Xi ~ N(0, 1) - независимые нормированные нормально распределенные СВ. Тогда X подчиняется распределению “хи”-квадрат с n степенями свободы: X ~ cn2. С ростом n “хи”-квадрат распределение приближается к нормальному с параметрами mX = n и sX = 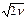 .
.
 2015-06-10
2015-06-10 261
261







