С целью упрощения математических преобразований, рассмотрим функцию двух аргументов 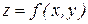 , предполагаю её достаточно гладкой, т.е. имеющей в достаточной окрестности точки (x, y) непрерывные производные первого порядка. Предположим также, что известны абсолютные
, предполагаю её достаточно гладкой, т.е. имеющей в достаточной окрестности точки (x, y) непрерывные производные первого порядка. Предположим также, что известны абсолютные 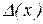 ,
, 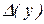 и относительные
и относительные 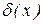 ,
, 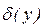 погрешности её аргументов. Поставим задачу определить абсолютную
погрешности её аргументов. Поставим задачу определить абсолютную 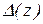 и относительную
и относительную 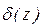 погрешности вычисления функции в точке (x, y).
погрешности вычисления функции в точке (x, y).
Оценим абсолютную величину погрешности функции. С этой целью, используя теорему Лагранжа, получим
 (1.9)
(1.9)
где 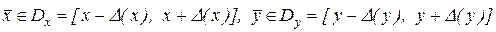 .
.
Используя, далее свойство модуля суммы, имеем
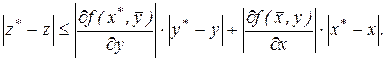 .
.
И, наконец, исключая зависимость оценки от неизвестных величин 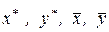 , получим
, получим
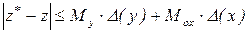 ,
,
где 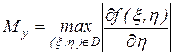 ,
, 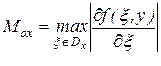 ,
,
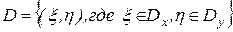 .
.
Обозначим
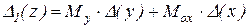 .
.
Если в начале преобразований (1.9) к исходному выражению прибавить 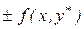 , то в результате аналогичных действий получим вторую оценку
, то в результате аналогичных действий получим вторую оценку
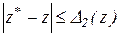 ,
,
где
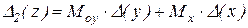 ,
,
где
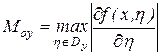 ,
, 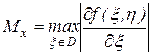 .
.
Тогда, очевидно, в качестве 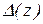 необходимо взять наименьшую из них, т.е. положить
необходимо взять наименьшую из них, т.е. положить
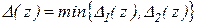 .
.
Если же допустить, что вполне естественно, достаточную малость абсолютных погрешностей 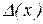
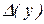 , то в качестве
, то в качестве 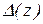 можно взять более простую, однако несколько завышенную оценку
можно взять более простую, однако несколько завышенную оценку
|
|
|
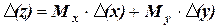 . (1.10)
. (1.10)
Действительно, в силу 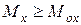 ,
, 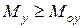 , очевидно
, очевидно 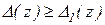 и
и 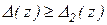 .
.
В этом случае из (1.10) для 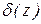 следует выражение
следует выражение
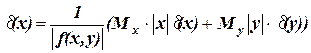 (1.11)
(1.11)
Аналогичным образом, для функции нескольких переменных 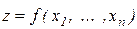 , получим
, получим
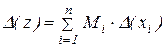
и
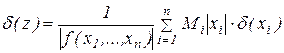 ,
,
где
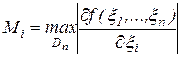 .
.
 2015-06-24
2015-06-24 393
393








