Наблюденное магнитное поле, представленное непрерывной кривой, можно дискретизировать, т.е. получить совокупность дискретных значений функции, взятой с определенным шагом дискретизации. Значения наблюденных величин, представленные в дискретном виде, удобны для использования в дальнейшем для компьютерной техники.
Заданные совокупностью дискретных значений магнитные поля подвергаются функциональным преобразованиям. Такие преобразования осуществляются с помощью дискретных преобразований Фурье. Дискретные преобразования Фурье исходят из обычных преобразований Фурье, но при этом операция интегрирования непрерывных функций переходит в операцию суммирования дискретных значений:
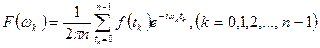 , (11.1)
, (11.1)
а также обратное преобразование
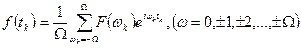 . (11.2)
. (11.2)
Здесь 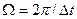 - период спектра дискретной функции, полученной при дискретизации исходной непрерывной функции f(t.) – (временной функции).
- период спектра дискретной функции, полученной при дискретизации исходной непрерывной функции f(t.) – (временной функции).
Формула (11.1) описывает Фурье-образ дискретной функции 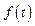 . На основе этой формулы находят соответствие (осуществляется отображение) между действительной функцией и комплексной функцией
. На основе этой формулы находят соответствие (осуществляется отображение) между действительной функцией и комплексной функцией 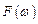 . Формула (11.2) позволяет вычислять действительную функцию (оригинал) по заданной комплексной функции
. Формула (11.2) позволяет вычислять действительную функцию (оригинал) по заданной комплексной функции 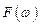 .
.
|
|
|
Из формул (11.1) и (11.2) видно, что суммы содержат совокупность гармонических колебаний 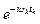 и
и 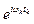 . Функции
. Функции 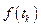 и F(ωk) играют роль амплитуд гармоник
и F(ωk) играют роль амплитуд гармоник
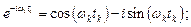
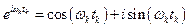 .
.
Представим формулы (11.1) и (11.2) в другом виде:
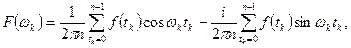 (11.3)
(11.3)
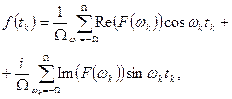 (11.4)
(11.4)
где
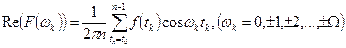 , (11.5)
, (11.5)
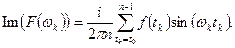 (11.6)
(11.6)
Здесь 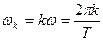 , а k – дискретная последовательность чисел, причем
, а k – дискретная последовательность чисел, причем 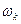 - частота, соответствующая моменту времени
- частота, соответствующая моменту времени 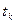 .
.
Ограничившись положительными значениями частоты 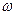 , получим формулу для обратного преобразования Фурье в таком виде:
, получим формулу для обратного преобразования Фурье в таком виде:
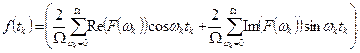 (11.7)
(11.7)
В формулах для заданной частоты 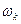
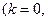
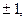
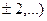 выполняем суммирование по всем заданным дискретным значениям исходной функции
выполняем суммирование по всем заданным дискретным значениям исходной функции 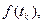 а именно
а именно 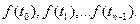 При применении формул отрезок задания функции
При применении формул отрезок задания функции 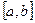 принимают за отрезок
принимают за отрезок 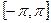 или
или 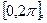 на котором рассматривается переменная
на котором рассматривается переменная 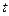 . Переменная круговая частота
. Переменная круговая частота 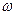 зависит от
зависит от 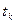 и изменяется на отрезке
и изменяется на отрезке 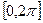 от 0 до
от 0 до 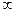 . Число изменений зависит от количества заданных дискретных значений функции. При этом
. Число изменений зависит от количества заданных дискретных значений функции. При этом 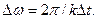
Вычисленные значения комплексной функции 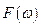 (комплексный спектр) позволяют найти модуль
(комплексный спектр) позволяют найти модуль 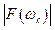 , т.е. амплитудный спектр и аргумент
, т.е. амплитудный спектр и аргумент 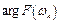 - фазовый спектр:
- фазовый спектр:
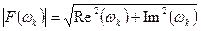 , (11.8)
, (11.8)
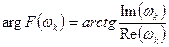 , (11.9)
, (11.9)
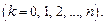
Таким образом, анализ по формулам (11.8) и (11.9) позволяет делать заключение о спектральном составе исходной функции, т.е. оригинала.
 2015-06-26
2015-06-26 440
440








