Знаходження екстремальних значень функції багатьох змінних

Методи знаходження екстремальних значень функції багатьох змінних 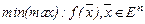можна розбити на дві групи.

Перша з них - це методи, в яких не використовуються похідні.

До другої належать методи, які використовують похідні для пошуку екстремальних значень функції 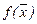, де 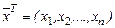- вектор змінних, який належить n-вимірному евклідовому простору .

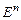Безградієнтні методи. Особливістю цих методів є те, що для їх реалізації не потрібно знати похідні функції 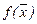. Ця перевага особливо відчутна у задачах з досить великим числом змінних, коли одержати похідні у вигляді аналітичних функцій досить складно. Крім того, методи цієї групи рекомендують застосовувати тоді, коли функції в деяких точках не мають похідних або мають розриви. Недолік цих методів - більш уповільнена швидкість збіжності порівняно із методами, які діють з першими та другими похідними функції f(x).

Симплексний метод. В основі цього методу лежить поняття симплексу. Нагадаємо, що симплексами є регулярні багатокутники в 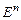.Наприклад, для n=2 регулярний симплекс ­– це рівносторонній трикутник (три точки) і т. д.

Координати вершин регулярного симплексу визначаються матрицею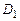

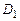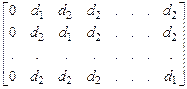= (6.1)

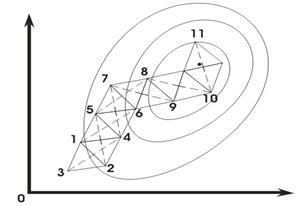
Рисунок 6.1 - Пошук мінімуму функції f(x) методом многокутників

в якої стовпців – вершини, пронумеровані від 1 до (n+1), а лінійки – їх координати.

Загальна кількість лінійок дорівнює числу незалежних змінних x ,

Елементи матриці 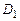визначаються за формулами

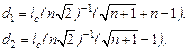(6.2)

де 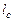- відстань між вершинами симплексу. Матриця 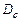визначає такий симплекс, одна з вершин якого перебуває на початку координат.

Щоб побудувати симплекс з вершиною в точці 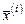, досить координати всіх вершин симплекса змістити на величину x ,

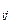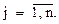
Обчислимо цільольову функцію у кожній з вершин симплексу. З вершини (точка 3), де значення функції максимальне проводиться проектуюча пряма через центр протилежної грані симплексу (рис. 6.1, пунктирна пряма). Будуємо новий симплекс, який включає одну нову вершину (точка 4), розміщену на проектуючій прямій симетрично відносно вершини 3. Ця операція називається відображенням, а новий симплекс — відображеним. Продовження цієї процедури, в якій кожний раз викреслюється вершина, де цільова функція максимальна, дає змогу визначити окіл мінімуму функції 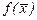. З рис. 6.1 випливає, що поблизу від точки мінімуму може виникнути зациклення (точки 10, 11). Для усунення цього явища змінюють розміри початкового симплексу до його зменшення. Критерієм закінчення пошуку можуть бути розміри симплексу: пошук припиняють, якщо всі ребра симплексу стануть менше наперед заданої достатньо малої величини.

Нехай на якомусь кроці обчислень одержаний многокутник з вершинами 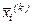, 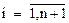. Визначимо вершину 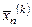з найбільшим значенням цільової функції

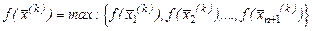
і вершини з найменшим значенням )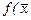

.

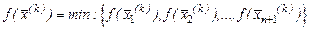Далі пошук вершин в 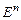, в якій 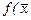) має мінімальне значення складається з наступних кроків.

Sp.1. Відображення (рис. 6.2) – проектування вершини 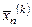, в якій функція 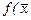) має найбільше значення, через центр протилежної грані симплексу:

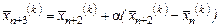(6.3)

Де α>0 – коефіцієнт відображення. Координати центру протилежної грані визначають за формулою

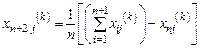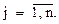, (6.4)

Рисунок 6.2 – Відображення

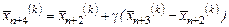Sp.2. Розтяг (рис. 6.3). Коли 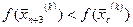, то вектор 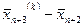розтягується в γ раз відповідно зі співвідношенням

(6.5)

де 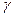>1 – коефіцієнт розтягу.

Якщ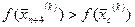о , то 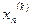замінюють на 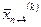і процедура продовжується, починаючи з Sp.1. В іншому випадку 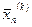замінюється на 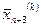і також здійснюється перехід до Sp.1.

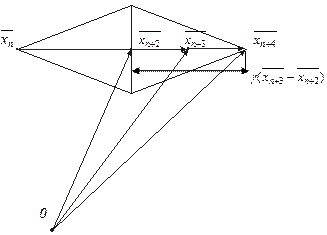
Рисунок 6.3 – Розтяг

Sp.3. Стиснення (рис. 6.4). Якщо 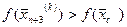для всіх 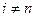то вектор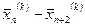
стискається у β раз відповідно за формулою

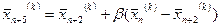, (6.6)

де 0< β >1 – коефіцієнт стиску. Потім 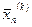замінюється на 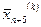і повертається до Sp.1 для продовження пошуку на k+1 кроці.

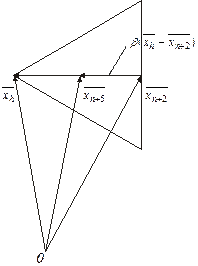
Рисунок 6.4 – Стиснення

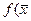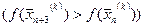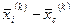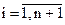
Sp.4. Редукція (рис. 6.5). Якщо в результаті виконання операції Sp.1 значення функції ) не зменшилось , всі вектори , зменшують у 2 рази у відповідності за формулою

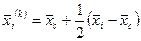
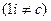
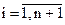(6.7)

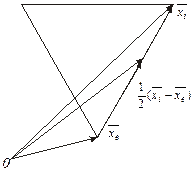
Рисунок 6.5 – Редукція

Потім повертаються до Sp.1 для продовження пошуку на k+1 кроці. Критерій закінчення ітерацій цього процесу полягає у перевірці умови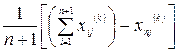

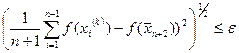, (6.8)

де 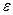- додатне число, що визначає точність розв’язку задачі. Рекомендоване значення коефіцієнта відображення α=1, а значення коефіцієнта розтягу 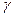і стиснення β лежать у межах: 2.8≤ ≤3, 0.4≤ β ≤06.

3 ЗАВДАННЯ

1 Написати основні співвідношення для мінімізації

методом Нелдера-Міда функції з таблиці завдань.

2 Провести оцінку числа обумовленості задачі мінімізації

для зазначеної в таблиці відносної похибки функції і

визначити максимально можливу точність обчислення

точки мінімуму.

3 Написати програму і на ЕОМ розрахувати з

максимально можливою точністю точку мінімуму

функції.

4 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

№	Функція f(x,у)	Початкові вершини	Відносна похибка df(x)
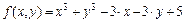
		(1,2),(2,0),(2,2)	10-8
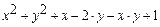
		(0,0),(2,0),(2,1)	10-8
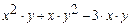
		(0,0),(2,0),(2,1)	10-9
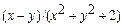
		(0,0),(0,1),(1,1)	10-9
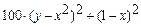
		(0,0),(1,0),(0,2)	10-8
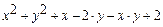
		(1,2),(2,0),(2,2)	10-9
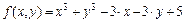
		(1,2),(2,0),(2,2)	10-8
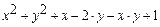
		(0,0),(2,0),(2,1)	10-8
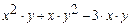
		(0,0),(2,0),(2,1)	10-9
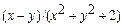
		(0,0),(0,1),(1,1)	10-9
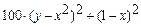
		(0,0),(1,0),(0,2)	10-8
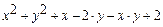
		(1,2),(2,0),(2,2)	10-9

5 КОНТРОЛЬНІ ПИТАННЯ

1 Етапи пошуку мінімуму функції.

2 Що таке локальний і глобальний мінімум?

3 Визначення унімодальної функції.

4 Абсолютне число обумовленості задачі мінімізації.

5 Симплекс-метод.