Метод найшвидшого спуску (Метод Коші)

Застосування цього методу для розв’язування задач мінімізації розглянуто ще французьким математиком Коші. Оскільки функція 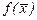зменшується в напрямку, протилежному до напрямку градієнта, то .

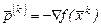Іноді замість градієнта функції 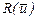вибирають нормований напрямок 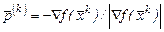. Таким чином, у методі найшвидшого спуску обчислювальна процедура утворюється за таким рекурентним співвідношенням:

,

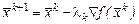або (7.2)

.

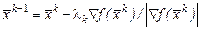Метод найшвидшого спуску лише тоді забезпечує високу швидкість збіжності, коли найбільше і найменше власне значення матриці Гессе значно відрізняється одне від одного.

Метод Ньютона. За цим методом для визначення методу пошуку застосовуються другі похідні, які мінімуму функція 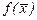повинна мати.

Нехай на k-му кроці пошуку незалежні змінні набувають значення 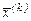; при переході до наступної ітерації 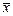зміниться на величину 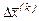. Розкладемо функцію 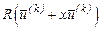в ряд Тейлора, обмежившись лінійними і квадратичними членами розкладу:

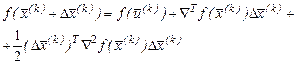. (7.3)

Визначимо мінімум функції 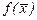відносно приросту 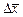. Для цього знаходимо градієнт функції 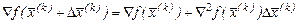, і прирівнюючи його до нульового вектора, одержимо:

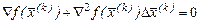. (7.4)

Якщо матриця Гессе не вироджена, то розв’язком (7.4) буде

.

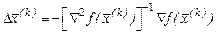Звідси випливає рекурентне правило, яке лежить в основі методу Ньютона:

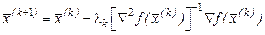. (7.5)

Метод Ньютона має квадратичну швидкість збіжності, а метод Коші тільки лінійну.

Вищу збіжність методу Ньютона обтяжує необхідність знаходження матриці Гессе. Щоб поєднати перевагу методу Коші (похідні лише першого порядку) з перевагою метода Ньютона (висока швидкість збіжності), розроблені методи, які носять назву квазіньютонівських.

Квазіньютонівські методи. Вони базуються на апроксимації матриці Гессе 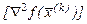так, що при цьому використовуються лише перші похідні. Ітерація методу Ньютона (3.5) замінюється на

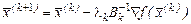, (7.6)

де 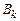- симетрична матриця розміром 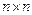. При 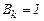(I – одинична матриця) – маємо градієнтний метод, а при 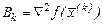- метод Ньютона.

В інших випадках 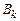вибирається так, щоб напрямок 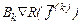був напрямком спуску при 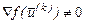. Ця умова виконується, якщо матриця 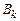додатно визначена.

Прийнято, що найефективнішою процедурою апроксимації матриці Гессе є процедура під назвою Брейдена – Глетчера – Гольтфарба – Шанно (BFGS - формула):

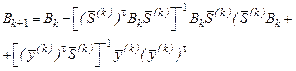. (7.7)

де 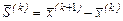- зміна вектора-змінної 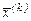на k -й ітерації: 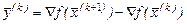- відповідна зміна градієнта. Початкове наближення 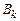, як правило, дорівнює одиничній матриці. При такому виборі матриці 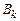перша ітерація квазіньютонівського пошуку еквівалентна кроку найшвидшого списку.

Метод спряжених градієнтів. В основі методу лежать властивості квадратичних функцій, і при побудові алгоритму обчислень теж використовують градієнти цільових функцій. Квадратична цільова функція n -незалежних

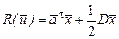. (7.8)

де D – симетрична додатно-визначена матриця; 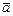- вектор, компоненти якого постійні величини, може бути мінімізована за n кроків (або менше), якщо кроки вибрані в так званих спряжених напрямках. Вектори 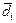і 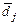називаються спряженими відносно симетричної матриці D, якщо 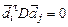для всіх .

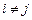3 ЗАВДАННЯ

1 Написати основні співвідношення для мінімізації

градієнтними методами функції з таблиці завдань.

2 Провести оцінку числа обумовленості задачі мінімізації

для зазначеної в таблиці відносної похибки функції і

визначити максимально можливу точність обчислення

точки мінімуму.

3 Написати програму і на ЕОМ розрахувати з

максимально можливою точністю точку мінімуму

функції.

4 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

№	Функція f(x,у)	Початкові вершини	Відносна похибка df(x)
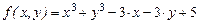
		(1,2)	10-8
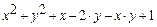
		(0,0.3)	10-8
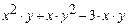
		(0.1,0.1)	10-9
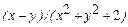
		(0.5,0.11)	10-9
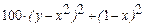
		(0,0)	10-8
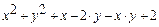
		(0,0.3)	10-9
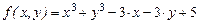
		(1,2)	10-8
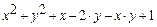
		(0,0.3)	10-8
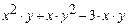
		(0.1,0.1)	10-9
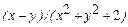
		(0.5,0.11)	10-9
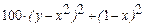
		(0,0)	10-8
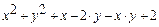
		(0,0.3)	10-9

5 КОНТРОЛЬНІ ПИТАННЯ

1 Етапи пошуку мінімуму функції.

2 Що таке локальний і глобальний мінімум?

3 Визначення унімодальної функції.

4 Абсолютне число обумовленості задачі мінімізації.

5 Градієнтні методи.