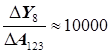Полученное уравнение регрессии в кодированных переменных имеет вид

Ў= 85,97+2,58х₁+0,57х₂+1,12х₃+0,19 х₁х₂ –

– 0,59 х₁х₃ – 0,92 х₂х₃ –0,70 х₁х₂х₃. (3.49)

Для перевода кодированного уравнения регрессии (3.49) в натуральную форму заменим каждый кодированный параметр х_J его формулой кодирования (3.31).

Для х₁ – времени реакции –

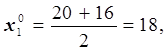
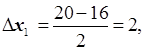
для х₂ – содержания ацетилацетилена в сырье –

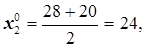
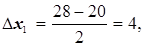
для х₃ – содержание уксусной кислоты в реакционной массе, %,

, .

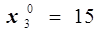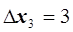Перевод уравнения (3.49) в натуральную форму выполним вводом формулы кодирования, тогда:

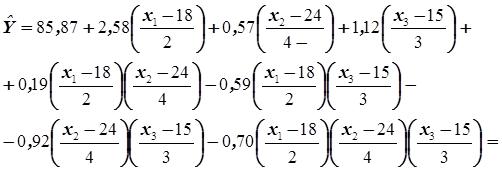
=198,94 – 8,3х₁ – 7,01х₂ – 8,62х₃ + 0,46х₁х₂ + 0,60х₁х₃ +

+ 0,45х₂х₃ – 0,03х₁х₂х₃.. (3.50)

Проверим результаты расчета по уравнениям (3.49) и (3.50) подстановкой соответствующих кодированных значений х_iJ и натуральных значений Х_iJ для одного из опытов, например, для восьмого опыта; очевидно, что расчетное 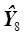должно быть равно опытному У₈ и равно 88,25.

Расчет по (3.49) дает величину 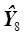= 88.22, близкую к фактическому У₈ = 88.25, однако расчет по (3.50) дает 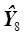= 79.4, явно не согласующееся с 88.25, причем расхождение между опытными и расчетными данными составляет 8.85 %, тогда как изменение результатов опытов в ходе эксперимента в целом лежало в пределах 90.4 – 81.08=9.32%. Ошибка при расчете по (3.50) связана с погрешностями расчета, возникающими при округлении промежуточных результатов калькуляторного расчета. Выполнение решения задачи на ЭВМ позволяет существенно облегчить расчетную часть задачи, одновременно избежать накопления погрешности расчета.

Расчет на ЭВМ коэффициентов уравнения дал следующее уравнение в кодированных переменных x_i:

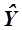= 85,97501+2,587501 x₁ + 0,5674992 x₂ + 1,124996 x₃ + +0,1950006 x₁x₂ – 0,5875006 x₁x₃ – 0, 9174976 x₂x₃ – 0,6950006 x₁x₂x₃,(3.49 а)

практически совпадающее (с точностью до второго знака после запятой) с (3.49), и уравнение в натуральных переменных X_i

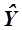= А₀ + А₁X₁ + А₂X₂ + А₃X₃ + А₁₂X₁X₂ ++ А₁₃X₁X₃ + А₂₃X₂X₃ +А₁₂₃X₁X₂X₃ =

= 197,8753 –8,24751 X₁ – 6, 968762 X₂ – 8,537517 X₃ + 0,4587505 X₁X₂ +

+0,5970839 X₁X₃ +0,4447923 X₂X₃ – 0,02895836 X₁X₂X₃, (3.50, а)

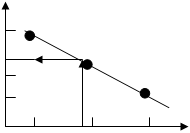в котором коэффициент А₀ = 197,8753 Ў ₈,%

отличается от А₀ = 198, 84 в уравнении 100

(3.50) почти на единицу, остальные коэф- 90 –

фициенты уравнений (3.50,а) и (3.50) имеют 80

достаточно близкие значения, при этом 70

результаты машинных расчетов дают по

уравнению (3.49,а) значение У для восьмо-

го опыта (табл. 3.5) Ў ₈= 88,25001 и по урав- 0.028 0.029 0.03 А₁₂₃

нению (3.50,а) Ў ₈=88,25003 практически Рис. 3.7. Влияние округления

совпадающие между собой. Следует отме- коэффициента А₁₂₃ на

тить, что весьма сильно влияет на погреш- расчет величины Ў ₈

ность расчета округление коэффициента

А₁₂₃ до 0.03 при эффекте тройного взаимодействия и уже незначительное округление величины А₁₂₃ приводит к ошибке расчете в несколько процентов (рис.3.7).

Если в ходе анализа уравнения регрессии, полученного по полному факторному эксперименту, окажется, что многие эффекты взаимодействия (особенно эффекты высших порядков – тройные, четверные и т.д.) оказываются незначимыми, то число опытов матрицы планирования оказывается больше числа коэффициентов уравнения регрессии и матрица планирования становится информационно ненасыщенной. Этот недостаток в значительной мере устраняется в дробных репликах от полного факторного эксперимента, позволяющих существенно уменьшить объем опытов при разработке уравнения регрессии.

Дробные реплики представляют собой часть матрицы планированияполного факторного эксперимента. Построение дробной реплики рассмотрим на базе матрицы планирования для двух факторов.

Допустим, что для двухфакторного процесса эффект взаимодействия х₁х₂ (табл. 3.3) незначим, тогда получается, что для нахождения трех коэффициентов 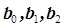выполнено четыре опыта. Чтобы максимально использовать эксперимент, заменим столбец параметра незначимого эффекта взаимодействия х₁х₂ на столбец нового параметра х₃, причем его кодированные значения примем такими же, что и коды исключенного столбца х₁х₂ (табл. 3.6). Естественно, такой подход к решению задачи расширяет возможности эксперимента -–теперь процесс исследуется по трем факторам вместо двух при том же числе опытов.

Таблица 3.6

К построению дробной реплики

N	х0	х1	х2	х1х2	х3	Y1
	+1	-1	+1	-1	-1	Y1,1
	+1	+1	+1	+1	+1	Y1,2
	+1	+1	-1	-1	-1	Y1,3
	+1	-1	-1	+1	+1	Y1,4

Полученная в табл. 3.6 матрица планирования, ни в чем не изменила своего содержания по кодам столбцов и сохраняет свойство ортогональности, что позволяет рассчитать уже четыре коэффициента уравнения регрессии (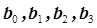) по уравнению (3.43). Полученная в таблице 3.6 матрица называется дробной репликой, то есть частью полного факторного эксперимента для трех факторов, который должен насчитывать восемь опытов (табл. 3.5). Рассмотренная дробная реплика дает уравнение регрессии вида:

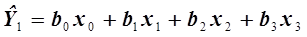. (3.51)

В общем случае для построения дробной реплики в матрице планирования полного факторного эксперимента достаточно исключить один или несколько столбцов эффектов взаимодействия, заменив их на столбцы новых исследуемых параметров процесса.

На первый взгляд, существенной экономии на проведение эксперимента мы не получили: полный факторный эксперимент для трех факторов включает восемь опытов, а дробная реплика (или полуреплика в нашем случае) лишь четыре. Однако при исследовании многофакторных процессов метод дробных реплик позволяет значительно сократить эксперимент. Так, например, для исследования процесса по семи факторам полный факторный эксперимент составляет 128 опытов, но если в трехфакторной матрице планирования все эффекты взаимодействия заменить на новые факторы (х₁х₂ на х₄ ,х₁х₃ на х₅, х₂х₃ на х₆, х₁х₂ х₃ на х₇), то для решения задачи нам придется выполнить лишь восемь опытов.

За экономичность дробной реплики приходится расплачиваться точностью расчета коэффициентов уравнения регрессии и отсутствием информации о влиянии эффектов взаимодействия на результат процесса (ведь при построении дробной реплики мы лишь предполагаем, что исключенные эффекты взаимодействия незначимы, а на самом деле они могут играть существенную роль). В случае реальной значимости эффектов взаимодействия они дают в дробной реплике эффект смешения с линейными коэффициентами и друг с другом. В самом деле, считая эффект взаимодействия х₁х₂ в табл. 3.6 незначимым, мы рассчитаем величину коэффициента 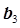как

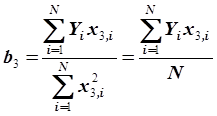. (3.52)

Допустим, что параметр х₃ вообще не влияет на результат процесса 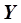(например, х₃ – это расход катализатора в процессе, однако изучаемое вещество на самом деле процесс не катализирует и является инертным), а вот эффект взаимодействия х₁х₂ на самом деле существует и влияет на 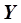. В этом случае мы практически рассчитаем не 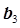, а :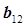

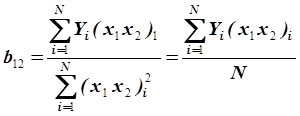, (3.53)

так как по условию дробной реплика коды столбцов х₁х₂ и х₃ совпадают. В этом случае рассчитанный коэффициент 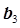стремится к величине генеральной оценки 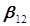коэффициента 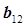, т.е. .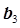

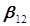В том случае, если значимы и параметр х₃, и эффект взаимодействия х₁х₂, они оба влияют на результат процесса 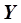и рассчитанный коэффициент 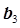стремится к сумме величин генеральных оценок 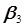коэффициента 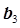и 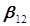коэффициента 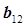, т.е.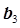 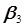+ 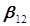, то есть мы получаем смешанную оценку коэффициента 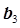. Поскольку новый параметр процесса х₃ может в свою очередь давать эффекты взаимодействия с остальными параметрами (х₁ и х₂), то, рассуждая аналогично, можно получить смешанные оценки и при расчете других коэффициентов уравнения регрессии.

Прогнозировать возможность появления смешанных оценок коэффициентов уравнения регрессии удобно при помощи понятия «определяющий контраст», представляющего собой выражение вида

х₁х₂х_3…х_К = 1, (3.54)

представляющем собой произведение кодированных параметров исключенного и введенного параметров. Для табл. 3.6 определяющий контраст составляет х₁х₂х₃ = 1. Умножая обе части уравнения определяющего контраста (3.54) на кодированный параметр любого столбца матрицы планирования х_i, получаем возможность обнаружения потенциального эффекта смешения; например, для столбца х₁ в матрице дробной реплики (табл.3.6):

х₁х₂х₃ = 1,

х₁ = х₂₁ (х₁х₂х₃) = х₁² х₂х₃,

а так как х₁² = 1, то

х₁ = х₂х₃,

то есть коды столбца х₁, совпадают с кодами возможного эффекта взаимодействия х₂х₃, который естественно не может быть включен в матрицу дробной реплики в связи с отсутствием в ней свободных столбцов, и расчетный коэффициент 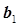может оказаться смешанным с коэффициентом 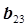, то есть 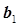стремится к сумме величин генеральных оценок 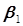коэффициента 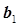и 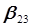коэффициента 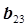, т.е. + .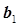

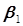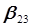В связи с появлением эффекта смешанных оценок коэффициентов, дробными репликами следует пользоваться с достаточной осторожностью, их обычно используют при наличии априорной информации об отсутствии конкретных эффектов взаимодействия в исследуемом процессе.

Методику подбора вида дробной реплики при разработке активного эксперимента рассмотрим на примере подготовки эксперимента по химическому превращению сырья с целью разработки линейного уравнения регрессии, включающего 4 параметра: x₁ – состав сырья, x₂ –температура процесса, x₃ –давление процесса, x₄ – удельный расход сырья, с использованием дробной реплики – полуреплики от полного факторного эксперимента первого порядка для четырех параметров, представляющей собой матрицу планирования для трех факторов (табл. 3.7); Y - выход целевого продукта в исследуемом процессе.

Таблица 3.7

Матрица планирования для трех факторов в кодированной форме

Номер опыта	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	Y
	+1 +1 +1 +1 +1 +1 +1 +1	+1 –1 –1 +1 +1 –1 –1 +1	+1 –1 +1 –1 +1 ­–1 +1 –1	+1 +1 +1 +1 –1 –1 –1 –1	+1 +1 –1 –1 +1 +1 –1 –1	+1 –1 –1 +1 –1 +1 +1 –1	+1 –1 +1 –1 –1 +1 –1 +1	+1 +1 –1 –1 –1 –1 +1 +1	Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8

Четвертый параметр заменяет собой один из парных эффектов взаимодействия или тройной эффект взаимодействия. Необходимо выяснить наиболее рациональный вариант ввода в матрицу четвертого параметра с точки зрения повышения уровня достоверности разрабатываемого уравнения регрессии.

Для решения этой задачи вначале уясним сущность смешанности оценок коэффициентов уравнения регрессии на базе генерирующего соотношения (например, x₄=x₁x₂ или x₄= x₁x₂x₃x₃) и соответствующих принятым генерирующим соотношениям определяющих контрастов x₁x₂x₃ =1и x₁x₂x₃x₄ =1.

В первом случае (x₄= x₁x₂) разрабатываемое уравнение регрессии будет иметь вид

Y = b₀+b₁x₁+ b₂ x₂+b₃ x₃+ b₄ x₄+ b₁₃ x₁ x₃+ b₂₃ x₂ x₃+ b₁₂₃ x₁x₂ x₃, (3.55)

во втором случае (x₄= x₁x₂ x₃) уравнение регрессии примет форму

Y = b₀+b₁x₁+ b₂ x₂+ b₃ x₃+ b₄ x₄+ b₁₂ x₁ x₂+ b₁₃ x₁ x₃+ b₂₃ x₂ x₃. (3..56)

Результаты расчета смешанных оценок коэффициентов b_{i ,}получаемых умножением обеих частей определяющего контраста на x_i, cведены в табл.3.8.

Таблица 3.8.