Рассмотрена замкнутая цилиндрическая оболочка, имеющая на одном конце жесткое закрепление, а на другом – свободный конец.
Оболочка находится под действием сосредоточенной нагрузки F, приложенной на свободном конце. Для оболочки принята своя система координат (рис. 2.1.).
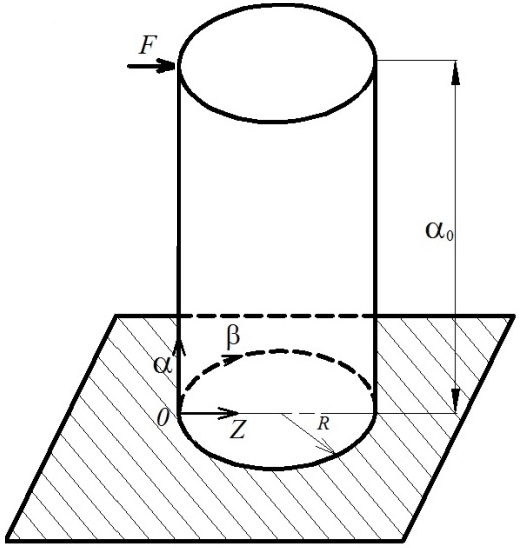
Рис.2.1.
Сосредоточенную нагрузку F разложим в тригонометрический ряд по переменной β:
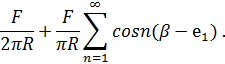
где 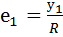 .
.
Выражения для перемещения, усилий и моментов при действии этого вида нагрузки при различных граничных условиях приведены в работе [1].
Так, выражение для определения радиального перемещения ω(a) для оболочки, имеющей жесткое закрепление и свободный конец, при действии нагрузки, определяемой членом ряда n =0, имеет вид:
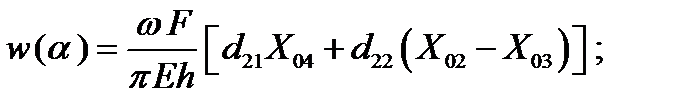
где
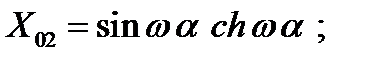
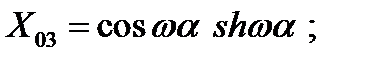
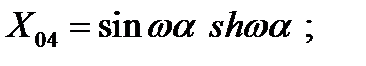
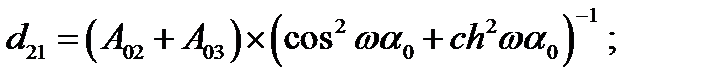
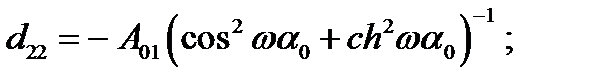
|
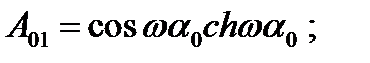
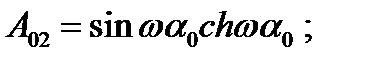
|
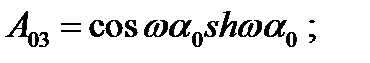
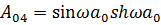 ; ;
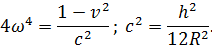
|
Выражения для определения радиальных перемещений w, при действии нагрузки, определяемой членом ряда n = 1,при рассматриваемых граничных условиях имеют вид:
при 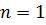
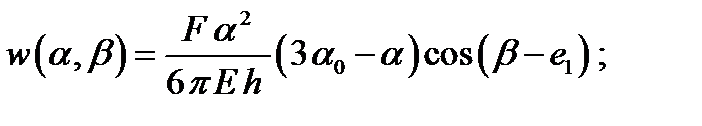 (2.3)
(2.3)
Радиальные перемещения, определяемые остальными членами тригонометрического ряда n 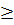 2, найдем, используя приближенную теорию оболочек в форме Гольденвейзера. [ ]
2, найдем, используя приближенную теорию оболочек в форме Гольденвейзера. [ ]
|
|
|
Основное разрешающее уравнение приближенной теории оболочек в форме Гольденвейзера имеет вид. (1.1)
при 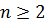
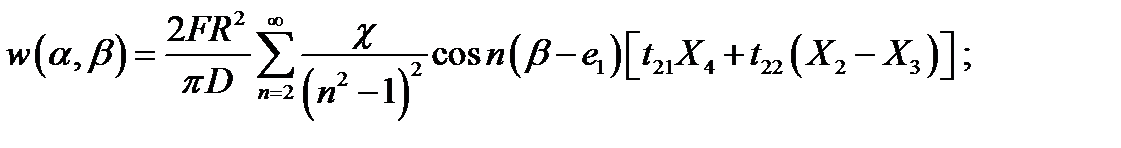
где
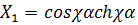 ;
;
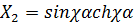 ;
;
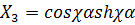 ;
;
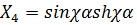 ;
;
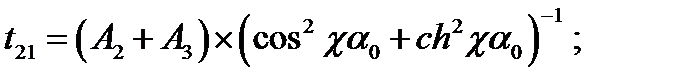
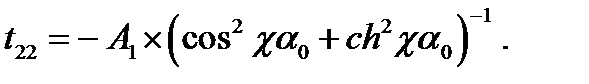
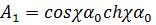 ;
;
 ;
;
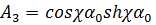 ;
;
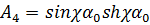 ;
;
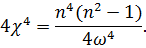
Расчет оболочки по этим формулам сводится к вычислению гиперболо-тригонометрических функций. При выполнении практических расчетов оболочек с использованием гиперболических функций при больших значениях аргументов появляется разность больших чисел. В этой случае в выражениях удобнее перейти от гиперболических функций к показательным функциям.
При 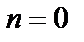
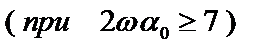 .
.
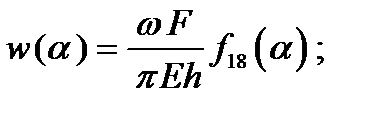
где
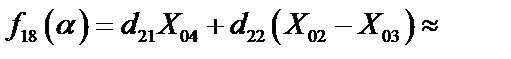
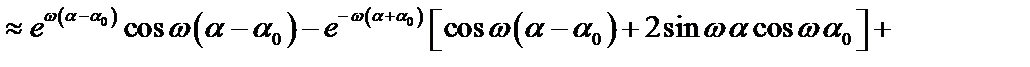
|
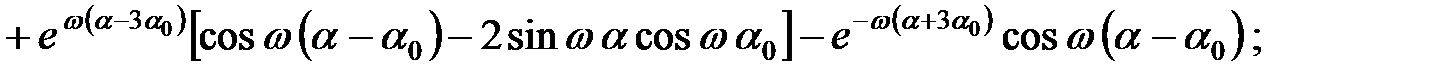
|
При 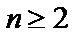 .
.
По приближенной теории 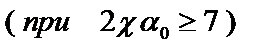 :
:
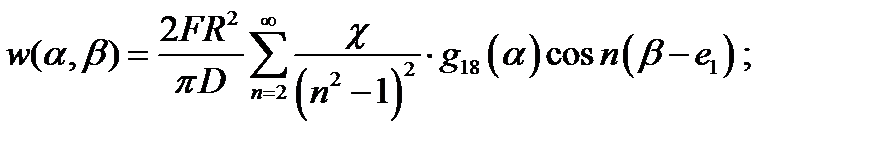
где
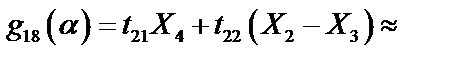
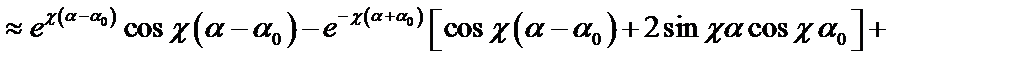
|
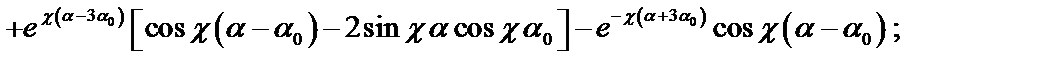
|
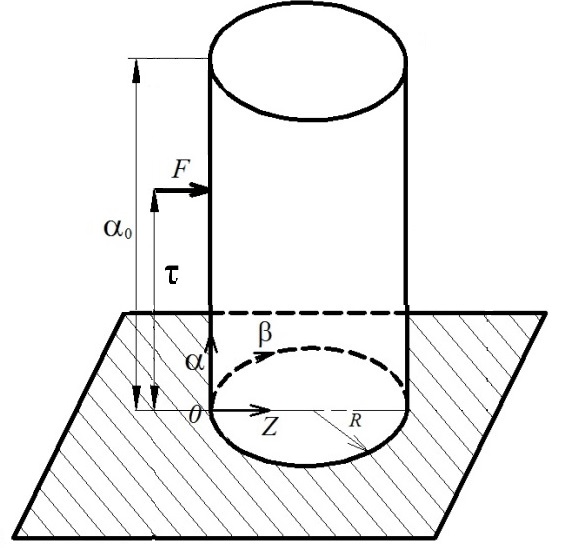
Рис. 2.2.
При действии сосредоточенной силы F в любой точке оболочки (рис. 2.2.) выражения для определения радиального перемещения w, определяемой членом ряда n =0,имеют вид:
При n = 0:
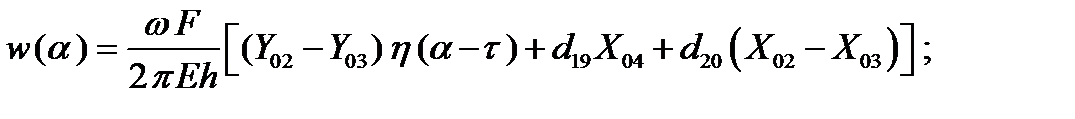
|
При n = 1:
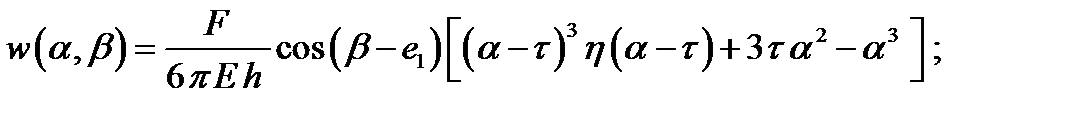
При n 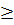 2:
2:
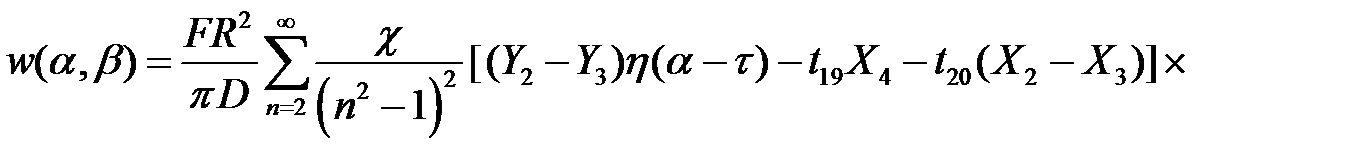
|
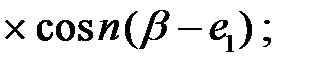
|
Расчет оболочки по этим формулам сводится к вычислению гиперболо-тригонометрических функций. При выполнении практических расчетов оболочек с использованием гиперболических функций при больших значениях аргументов появляется разность больших чисел. В этой случае в выражениях удобнее перейти от гиперболических функций к показательным функциям.
При n = 0 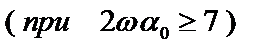 :
:
На участке 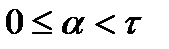 :
:
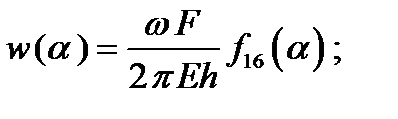
где
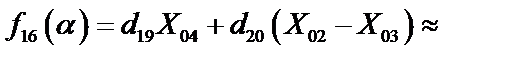
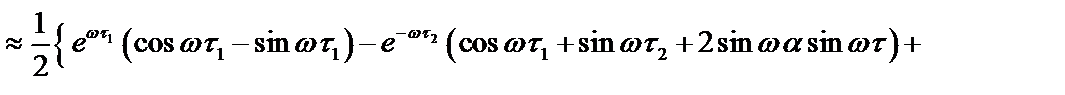
|
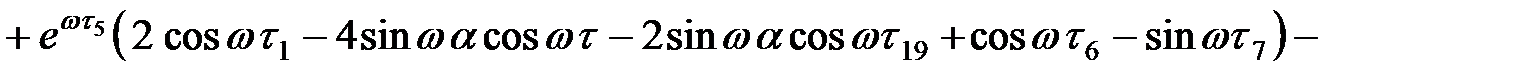
|
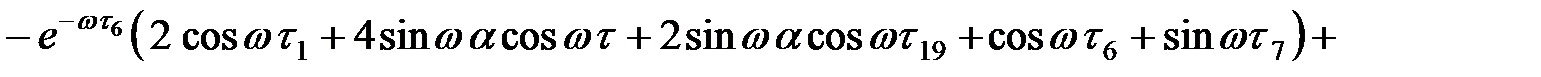
|
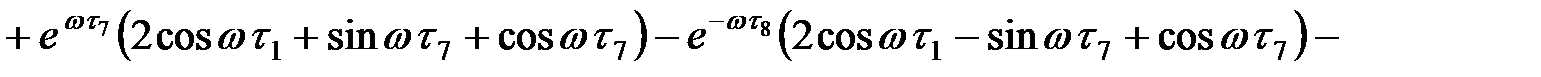
|
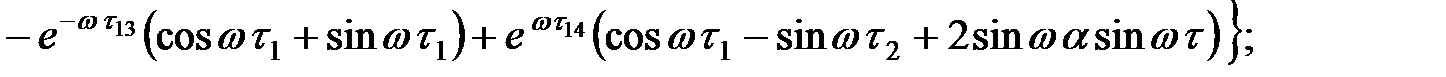
|
На участке 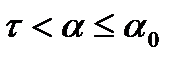 :
:
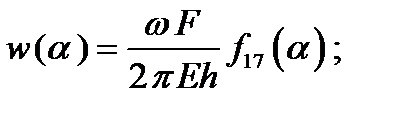
где
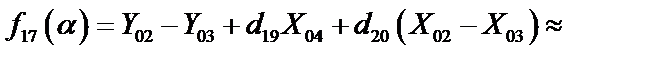
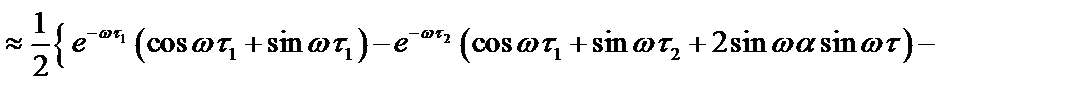
|
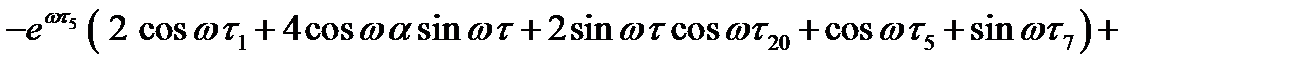
|
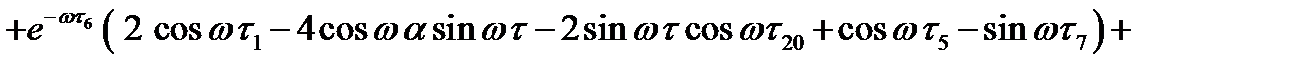
|
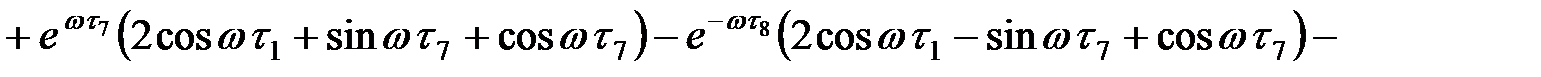
|
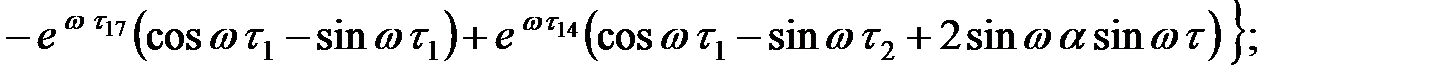
|
В качестве 1-го примера произведен расчет замкнутой цилиндрической оболочки со следующими геометрическими параметрами: длина оболочки L=30 м, радиус R=6 м, α0=L/R=5, толщина стенки h=0,24 м, коэффициент Пуассона v=0,2. Оболочка нагружена сосредоточенной нагрузкой F, расположенной на свободном конце оболочки.
|
|
|
На рис.2.3 приведен график изменения величины радиального перемещения 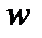 в точке приложения сосредоточенной силы
в точке приложения сосредоточенной силы 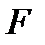 в зависимости от количества членов ряда n.
в зависимости от количества членов ряда n.
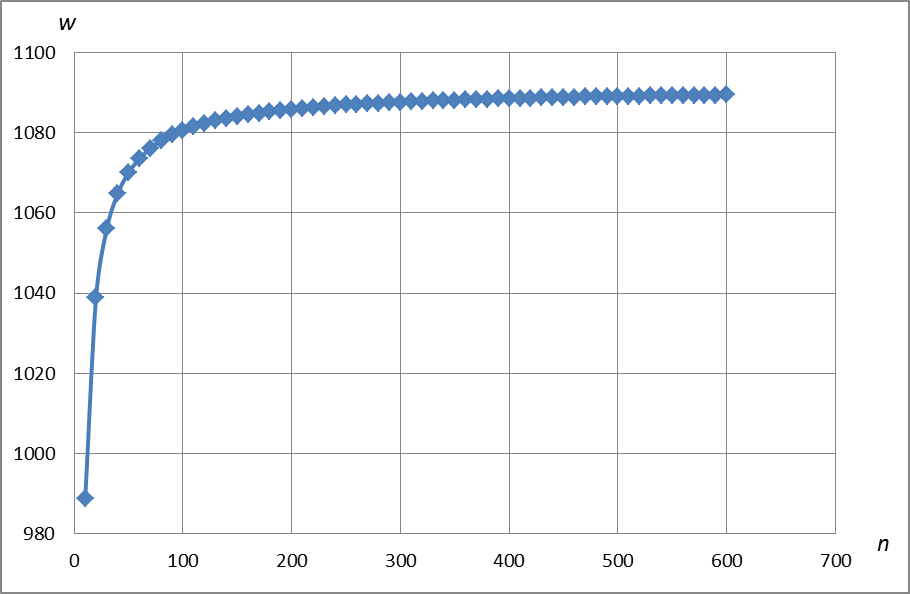
| Рис. 2.3. |
На рис. 2.4 приведен график изменения величины радиального перемещения 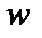 в точке
в точке 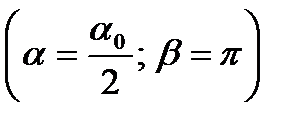 в зависимости от количества членов ряда n.
в зависимости от количества членов ряда n.
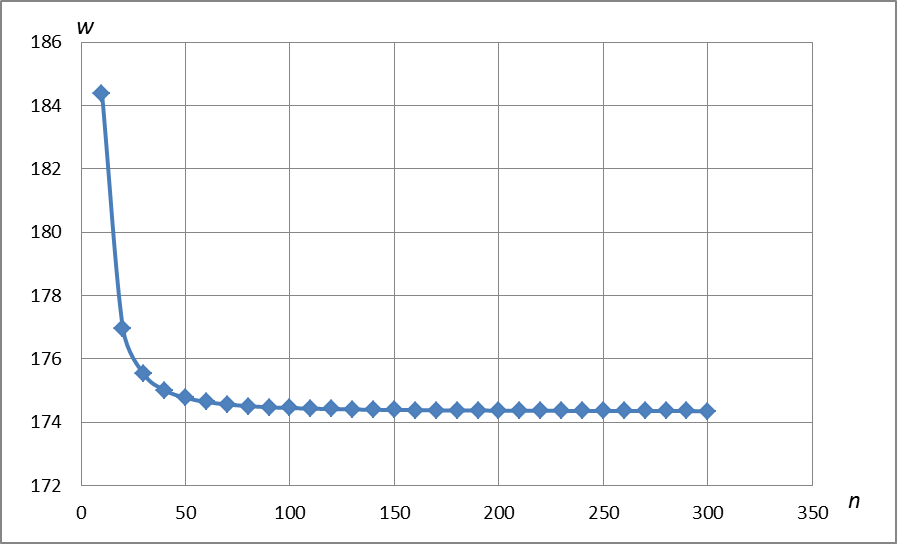
| Рис. 2.4. |
Радиальные перемещения в различных точках вдоль образующих 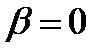 и и 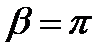
| |||||||||||||
| α0/12 | 2α0/12 | 3α0/12 | 4α0/12 | 5α0/12 | 6α0/12 | 7α0/12 | 8α0/12 | 9α0/12 | 10α0/12 | 11α0/12 | α0 | ||
| Местоположение внешней сосредоточенной нагрузки τ | α0/12 | 437,2272 | 129,0455 | 75,6900 | 52,7608 | 40,8291 | 33,9563 | 29,7344 | 26,9918 | 25,0751 | 23,5877 | 22,2855 | 21,0333 |
| 13,0853 | -0,1977 | 0,5575 | 1,1005 | 1,4228 | 1,8251 | 3,6728 | 7,3014 | 11,9535 | 16,8692 | 21,7229 | 26,5107 | ||
| 2α0/12 | 127,8881 | 633,5324 | 285,9954 | 200,1550 | 156,2153 | 130,9713 | 115,5931 | 105,8045 | 99,1998 | 94,2878 | 90,1219 | 86,1622 | |
| -1,3550 | 14,0506 | 1,9572 | 4,0614 | 6,1231 | 9,9770 | 17,6298 | 30,0670 | 46,0735 | 63,6193 | 81,4304 | 99,1818 | ||
| 3α0/12 | 75,7717 | 283,8347 | 797,6617 | 437,8243 | 338,8618 | 285,0053 | 253,0995 | 233,4691 | 220,8916 | 212,1320 | 205,0917 | 198,5365 | |
| 0,6392 | -0,2037 | 18,2653 | 8,7603 | 15,8784 | 27,3576 | 45,0651 | 69,5620 | 100,2274 | 134,8396 | 171,0212 | 207,5109 | ||
| 4α0/12 | 52,7561 | 200,2948 | 435,0713 | 955,8153 | 595,1904 | 494,3698 | 439,5793 | 407,9065 | 389,2076 | 377,5698 | 369,1667 | 361,6941 | |
| 1,0957 | 4,2012 | 6,0073 | 31,1960 | 32,6799 | 55,7808 | 86,8859 | 126,2109 | 173,0675 | 226,1238 | 282,8231 | 340,6736 | ||
| 5α0/12 | 40,8294 | 156,2079 | 339,0149 | 592,6639 | 1123,7231 | 770,6040 | 676,6843 | 628,9555 | 604,3047 | 591,9103 | 585,1671 | 580,0768 | |
| 1,4230 | 6,1157 | 16,0315 | 30,1534 | 72,6503 | 95,7277 | 142,7801 | 198,8162 | 263,0928 | 334,2109 | 410,2169 | 488,2056 | ||
| 6α0/12 | 33,9563 | 130,9716 | 284,9990 | 494,4823 | 768,9669 | 1334,3922 | 978,7130 | 900,5900 | 868,3562 | 857,9601 | 857,4653 | 859,8949 | |
| 1,8251 | 9,9772 | 27,3512 | 55,8933 | 94,0906 | 161,4943 | 211,5105 | 285,5155 | 367,5558 | 455,8798 | 548,0968 | 641,9298 | ||
| 7α0/12 | 29,7345 | 115,5932 | 253,0996 | 439,5768 | 676,7301 | 978,0163 | 1549,7629 | 1238,9533 | 1187,6253 | 1181,0644 | 1193,0956 | 1210,6047 | |
| 3,6728 | 17,6298 | 45,0652 | 86,8834 | 142,8259 | 210,8138 | 306,0744 | 383,7697 | 483,1168 | 586,8715 | 692,4741 | 798,1951 | ||
| 8α0/12 | 26,9919 | 105,8045 | 233,4692 | 407,9063 | 628,9572 | 900,5890 | 1238,6012 | 1849,1979 | 1580,2376 | 1571,3253 | 1603,7019 | 1647,6536 | |
| 7,3014 | 30,0670 | 69,5620 | 126,2107 | 198,8178 | 285,5146 | 383,4175 | 505,2276 | 605,7703 | 722,9738 | 840,1673 | 957,1429 | ||
| 9α0/12 | 25,0751 | 99,1999 | 220,8916 | 389,2076 | 604,3043 | 868,3594 | 1187,6295 | 1579,3972 | 2252,3448 | 2051,2495 | 2109,5192 | 2198,3818 | |
| 11,9535 | 46,0735 | 100,2274 | 173,0675 | 263,0924 | 367,5590 | 483,1211 | 604,9299 | 746,1984 | 860,8467 | 989,7237 | 1118,4084 | ||
| 10α0/12 | 23,5878 | 94,2878 | 212,1320 | 377,5698 | 591,9103 | 857,9597 | 1181,0654 | 1571,3833 | 2049,4238 | 2830,2030 | 2750,1184 | 2917,9665 | |
| 16,8692 | 63,6193 | 134,8396 | 226,1238 | 334,2110 | 455,8795 | 586,8725 | 723,0318 | 859,0210 | 1013,6590 | 1140,1423 | 1280,9074 | ||
| 11α0/12 | 22,2855 | 90,1220 | 205,0917 | 369,1667 | 585,1671 | 857,4653 | 1193,0955 | 1603,6987 | 2109,6417 | 2747,4998 | 3759,2654 | 3946,6948 | |
| 21,7229 | 81,4304 | 171,0212 | 282,8231 | 410,2169 | 548,0968 | 692,4739 | 840,1640 | 989,8463 | 1137,5236 | 1305,2504 | 1440,4182 | ||
| α0 | 21,0333 | 86,1622 | 198,5365 | 361,6941 | 580,0768 | 859,8949 | 1210,6047 | 1647,6536 | 2198,3818 | 2917,9665 | 3946,6948 | 6764,3713 | |
| 26,5107 | 99,1818 | 207,5109 | 340,6736 | 488,2056 | 641,9298 | 798,1951 | 957,1429 | 1118,4084 | 1280,9074 | 1440,4182 | 1658,7121 |
Значения, приведенные на рис. 2.3 и рис. 2.4, необходимо умножить на 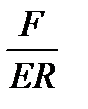 . Из графиков видно, что при определении радиального перемещения
. Из графиков видно, что при определении радиального перемещения 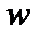 в точке приложения сосредоточенной силы
в точке приложения сосредоточенной силы 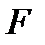 достаточно в тригонометрическом ряду (1) удерживать 300 членов ряда, а при определении радиального перемещения
достаточно в тригонометрическом ряду (1) удерживать 300 членов ряда, а при определении радиального перемещения 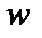 в точках на образующей
в точках на образующей 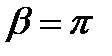 –
–
100 членов ряда.
Далее были взяты 12 точек приложения внешней сосредоточенной радиальной нагрузки F (τ= α0/12 … τ= 11α0/12) и 12 точек, в которых определялась величина радиального перемещения 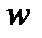 при
при 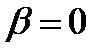 и при
и при 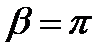 . Полученные результаты сведены в таблицу 1.
. Полученные результаты сведены в таблицу 1.
Таблица 1.
В числителе указана величина радиального перемещения 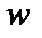 при
при 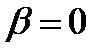 , в знаменателе - при
, в знаменателе - при 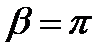 . Значения, приведенные в таблице 1, необходимо умножить на
. Значения, приведенные в таблице 1, необходимо умножить на 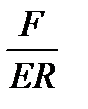 .
.
Посмотрим, как изменяется величина радиального перемещения 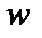 при изменении геометрических параметров оболочки. Проделав аналогичные операции, был выполнен расчет замкнутой цилиндрической оболочки со следующими геометрическими параметрами: длина оболочки L=30 м, радиус R=3 м, α0=L/R=10, толщина стенки h=0,16 м, коэффициент Пуассона v=0,2. Оболочка нагружена сосредоточенной радиальной нагрузкой F, расположенной на расстоянии τ. Оболочка по концам шарнирно закреплена (рис. 2.1).
при изменении геометрических параметров оболочки. Проделав аналогичные операции, был выполнен расчет замкнутой цилиндрической оболочки со следующими геометрическими параметрами: длина оболочки L=30 м, радиус R=3 м, α0=L/R=10, толщина стенки h=0,16 м, коэффициент Пуассона v=0,2. Оболочка нагружена сосредоточенной радиальной нагрузкой F, расположенной на расстоянии τ. Оболочка по концам шарнирно закреплена (рис. 2.1).
Были взяты 11 точек приложения внешней сосредоточенной радиальной нагрузки F (τ= α0/12 … τ= 11α0/12) и 11 точек, в которых определялась величина радиального перемещения 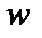 при
при 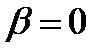 и при
и при 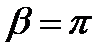 . Полученные результаты сведены в таблицу 2.
. Полученные результаты сведены в таблицу 2.
|
|
|
Таблица 2.
Радиальные перемещения в различных точках вдоль образующих 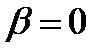 и и 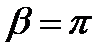
| |||||||||||||
| α0/12 | 2α0/12 | 3α0/12 | 4α0/12 | 5α0/12 | 6α0/12 | 7α0/12 | 8α0/12 | 9α0/12 | 10α0/12 | 11α0/12 | α0 | ||
| Местоположение внешней сосредоточенной нагрузки τ | α0/12 | 334,5614 | 102,4611 | 62,2975 | 44,9283 | 35,7054 | 30,1745 | 26,5026 | 23,6696 | 21,0564 | 18,4084 | 15,6993 | 12,9670 |
| 8,5098 | -0,6884 | 0,6952 | 9,1871 | 15,3195 | 13,6056 | 7,2778 | -0,3606 | -7,8293 | -14,7964 | -21,4014 | -27,8761 | ||
| 2α0/12 | 102,5150 | 492,8048 | 232,9832 | 168,8141 | 135,3483 | 115,2874 | 101,9019 | 91,7191 | 82,7425 | 73,9704 | 65,1040 | 56,1725 | |
| -0,6345 | 9,4990 | 11,9569 | 29,3166 | 43,0758 | 41,0532 | 23,3213 | -1,6740 | -28,0171 | -53,5293 | -78,0966 | -102,2737 | ||
| 3α0/12 | 62,2969 | 232,9235 | 632,1076 | 364,3034 | 290,1859 | 248,0251 | 220,4543 | 200,1062 | 183,0898 | 167,2700 | 151,6584 | 136,0139 | |
| 0,6946 | 11,8972 | 40,9903 | 53,2359 | 65,5488 | 62,5776 | 37,4889 | -5,5921 | -56,1827 | -107,8518 | -158,7002 | -209,0166 | ||
| 4α0/12 | 44,9283 | 168,8119 | 364,3616 | 770,0021 | 501,5251 | 424,1635 | 377,8416 | 345,7783 | 320,8431 | 299,2345 | 278,8445 | 258,7052 | |
| 9,1871 | 29,3144 | 53,2940 | 80,3198 | 77,8056 | 66,9893 | 36,5611 | -17,6175 | -90,1113 | -170,1622 | -251,6319 | -332,9665 | ||
| 5α0/12 | 35,7054 135,3483 | 135,3483 | 290,1853 | 501,4613 | 914,6363 | 649,2801 | 573,1264 | 527,3920 | 495,8763 | 471,5489 | 450,4414 | 430,2645 | |
| 15,3195 | 43,0758 | 65,5482 | 77,7418 | 83,6103 | 54,1750 | 13,6918 | -47,3499 | -132,1947 | -235,1483 | -345,5510 | -457,4870 | ||
| 6α0/12 | 30,1745 | 115,2874 | 248,0251 | 424,1613 | 649,3424 | 1080,9972 | 814,9294 | 746,8632 | 709,7101 | 687,0336 | 671,0267 | 657,0558 | |
| 13,6056 | 41,0532 | 62,5776 | 66,9871 | 54,2374 | 31,1990 | -28,3700 | -99,0766 | -189,4899 | -302,1959 | -430,9271 | -564,8240 | ||
| 7α0/12 | 26,5026 | 101,9019 | 220,4543 | 377,8416 | 573,1258 | 814,8615 | 1254,3803 | 1015,1859 | 966,8313 | 950,1372 | 946,7274 | 947,2926 | |
| 7,2778 | 23,3213 | 37,4889 | 36,5611 | 13,6912 | -28,4379 | -80,5890 | -168,1242 | -264,0731 | -375,4827 | -503,0130 | -639,1866 | ||
| 8α0/12 | 23,6696 | 91,7191 | 200,1062 | 345,7783 | 527,3920 | 746,8610 | 1015,2522 | 1485,0049 | 1280,1580 | 1268,3148 | 1286,6487 | 1313,5147 | |
| -0,3606 | -1,6740 | -5,5921 | -17,6175 | -47,3499 | -99,0788 | -168,0579 | -243,7355 | -349,0489 | -454,3917 | -563,4591 | -675,1768 | ||
| 9α0/12 | 21,0564 | 82,7425 | 183,0898 | 320,8431 | 495,8763 | 709,7101 | 966,8306 | 1280,0862 | 1803,0112 | 1657,5696 | 1705,9133 | 1777,0857 | |
| -7,8293 | -28,0171 | -56,1827 | -90,1113 | -132,1947 | -189,4899 | -264,0738 | -349,1207 | -430,9568 | -529,6350 | -613,2536 | -689,0523 | ||
| 10α0/12 | 18,4084 | 73,9704 | 167,2700 | 299,2345 | 471,5489 | 687,0336 | 950,1372 | 1268,3127 | 1657,6398 | 2273,3959 | 2233,6004 | 2380,1356 | |
| -14,7964 | -53,5293 | -107,8518 | -170,1622 | -235,1483 | -302,1959 | -375,4827 | -454,3938 | -529,5649 | -586,9488 | -651,7701 | -705,8355 | ||
| 11α0/12 | 15,6993 | 65,1040 | 151,6584 | 278,8445 | 450,4414 | 671,0267 | 946,7274 | 1286,6487 | 1705,9113 | 2233,3720 | 3043,5641 | 3231,5938 | |
| -21,4014 | -78,0966 | -158,7002 | -251,6319 | -345,5510 | -430,9271 | -503,0130 | -563,4590 | -613,2556 | -651,9986 | -679,2367 | -724,4106 | ||
| α0 | 12,9670 | 56,1725 | 136,0139 | 258,7052 | 430,2645 | 657,0558 | 947,2926 | 1313,5147 | 1777,0857 | 2380,1356 | 3231,5938 | 5445,1622 | |
| -27,8761 | -102,2737 | -209,0166 | -332,9665 | -457,4870 | -564,8240 | -639,1866 | -675,1768 | -689,0523 | -705,8355 | -724,4106 | -708,9653 |
В числителе указана величина радиального перемещения 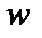 при
при 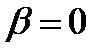 , в знаменателе - при
, в знаменателе - при 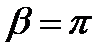 . Значения, приведенные в таблице 1, необходимо умножить на
. Значения, приведенные в таблице 1, необходимо умножить на 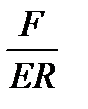 .
.
|
|
|
 2015-08-21
2015-08-21 801
801








