В газовой динамике движение газа рассматривается как движение сплошной Среды, заполняющей все исследуемое пространство без образования пустот. Обычно параметры газа в разных точках пространства существенно отличаются друг от друга и такой газ является неравновесным. В классической термодинамике параметры неравновесного термодинамического тела (газа) вообще не подлежат рассмотрению. Поэтому в газодинамике важным является понятия элемента сплошной среды, объем которого настолько мал, что его можно считать точкой и настолько велик, чтобы содержащихся в нем частицу хватило для введения среднестатистических параметров газа. Данные элементы среды принято считать равновесными и для описания изменения их состояния за счет деформации и теплообмена можно применять уравнения равновесной термодинамики.
Таким образом движение газа можно рассматривать как механическое перемещение элементов среды изменяющих свое термодинамическое состояние.
Движение элементов среды описывается с помощью двух уравнений механики, отражающих законы сохранения массы и импульса, которые в газодинамике называются уравнениями неразрывности и количества движения.
|
|
|
Изменение состояния выделенных элементов описывается с помощью уравнения состояния и первого закона термодинамики, выражающего собой закон сохранения энергии. Обычно это уравнение преобразуется в уравнение изменения кинетической и внутренней энергии и в газовой динамике называется уравнением энергии.
Таким образом три дифференциальных уравнения, отражающих законы сохранения массы, импульса и энергии и алгебраическое уравнение состояния, составляют полную систему уравнений, позволяющих при известных начальных и граничных условиях определить параметры состояния газа (давление, температуру и плотность) и вектор скорости газа в каждой точке исследуемого пространства в каждый момент времени.
При изучении движения сплошной среды используются два метода: метод Лагранжа и метод Эйлера.
В методе Лагранжа отдельные частицы рассматривают как материальные точки, сплошь заполняющие некий вещественный объем. Изучение движения заключается в определении скорости, ускорения частиц и параметров состояния газа как функции времени и в исследовании изменения их при переходе от частицы к частице.
При таком подходе координаты (x, y, z) любой частицы жидкого объема в момент времени t можно рассматривать как функции времени и начального положения той же частицы (x0, y0, z0):
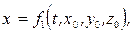
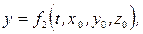
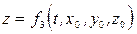
Вместо декартовых координат 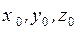 можно взять любые три величины
можно взять любые три величины 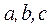 связанные с
связанные с 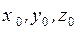 однозначными зависимостями, тогда x, y, z можно представить в виде функций от переменных Лагранжа
однозначными зависимостями, тогда x, y, z можно представить в виде функций от переменных Лагранжа 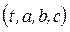 . Составляющие скорости и ускорения определяются как первые и вторые производные от координат:
. Составляющие скорости и ускорения определяются как первые и вторые производные от координат:
|
|
|

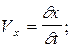

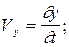
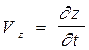
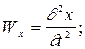
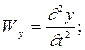
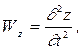
где 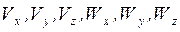 –– проекции скорости
–– проекции скорости 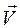 и ускорения
и ускорения 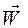 на оси x, y, z.
на оси x, y, z.
В методе Эйлера следует за изменением параметров газа в каждой отдельной точке исследуемого пространства то есть наблюдают за изменением во времени параметров движения частицы (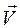 ,
, 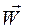 ), проходящей через фиксированную точку пространства и за изменением их при переходе из одной тоски пространства в другую.
), проходящей через фиксированную точку пространства и за изменением их при переходе из одной тоски пространства в другую.
Таким образом при таком подходе скорость, ускорение, плоскость и другие параметры частиц будут функциями времени и координат:
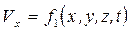 ,
,
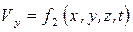 ,
,
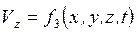
Для каждой частицы жидкости 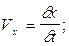
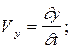
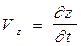 , где
, где 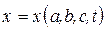 ;
; 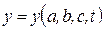 ;
; 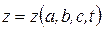 .
.
При определении ускорения в переменных Эйлера надо учитывать как изменение скорости в данной тоске во времени, так и то, что через данную тоску проходят разные частицы. То есть, если частица в момент времени 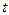 имела координаты
имела координаты 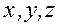 и скорость
и скорость 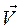 , то за время
, то за время 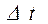 она переместиться в положение
она переместиться в положение 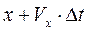 ,
, 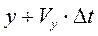 ,
, 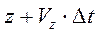 и скорость ее станет
и скорость ее станет
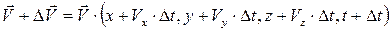
Тогда ускорение, характеризующее изменение скорости вдоль траектории движения частицы определится:
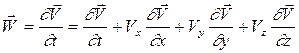
3.5. Простые волны
Как мы выяснили ранее, простые римановские волны описываются особыми решениями основной системы дифференциальных уравнений в виде (3.34), (3.35) для совершенного газа:
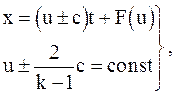 (3.43)
(3.43)
где знаки выбираются следующим образом. Если волна распространяется вправо, в положительном направлении оси ox, то выбираются верхние знаки; если влево, в отрицательном направлении оси ox, то выбираются нижние знаки.
Рассмотрим характеристики простых волн.
Как было установлено, выражение (с плюсом или минусом):
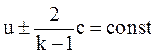 (3.44)
(3.44)
является характеристикой решений основной системы в плоскости u, c и представляет собой прямую линию. Так как мы рассматриваем одно уравнение (при решении конкретной задачи), то характеристика для данного особого решения - одна прямая линия, вдоль которой переносится постоянное значение выражения, например, (рис.3.5)
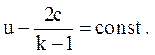 Характеристики простой волны (3.43) в общем случае в плоскости x, t имеют вид (для системы с верхними знаками)
Характеристики простой волны (3.43) в общем случае в плоскости x, t имеют вид (для системы с верхними знаками)
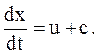 (3.45) (3.45)
|  Рис. 3.5. Характеристика особого решения
Рис. 3.5. Характеристика особого решения
|
Возьмем на характеристике в плоскости u, c какую-нибудь точку 3. Эта точка будет определять состояние среды с фиксированными u1 и c3. Для данного фиксированного состояния имеем уравнение характеристики в плоскости x, t:
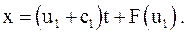 (3.46)
(3.46)
Продифференцируем это выражение и получим скорость распространения данного фиксированного состояния среды
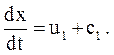
Итак, для каждого данного фиксированного состояния среды i в плоскости x, t имеем определенную прямую линию. Для другого фиксированного состояния будем иметь в плоскости x, t другую прямую линию (рис. 3.6).
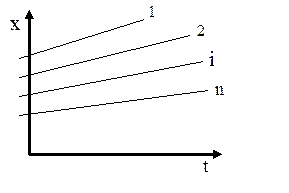 Рис. 3.6. Семейство характеристик Рис. 3.6. Семейство характеристик
| Таким образом, каждой точке характеристики в плоскости u, c соответствует определенная характеристика в плоскости x, t. Далее рассмотрим несколько задач газовой динамики, которые описываются теорией простых римановских волн. |
3.6. Волны сжатия
| Пусть мы имеем жесткую трубу с поршнем. В начальный момент времени поршень покоится и справа от него в трубе находится покоящийся совершенный газ с параметрами Pн, r н, cн (рис.3.7а). Затем поршень начинает вдвигаться в трубу. От поршня вправо по | 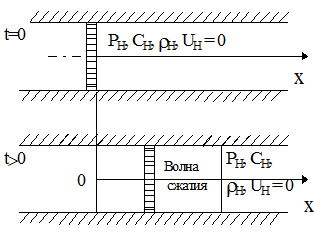 Рис. 3.7. Расчетная схема (а, б) Рис. 3.7. Расчетная схема (а, б)
|
газу пробежит волна сжатия. Движение газа в данном случае является плоским изоэнтропическим и граничит с областью покоя. Такое движение газа представляет собой простую волну и описывается особым решением.
Из двух особых решений данной задачи выбираем одно решение, при этом пользуемся правилом: если волны идут в положительном направлении оси ox, то выбираем особое решение из (3.43) с верхними знаками
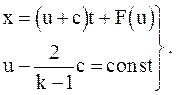 (3.47)
(3.47)
Величину константы определяем из граничных условий на фронте волны uн= 0, c = cн (см. рис. 3.7б)
|
|
|
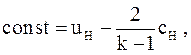 (3.48)
(3.48)
так как uH=0 (газ покоится), константа в нашем случае будет равна
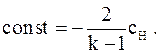 (3.49)
(3.49)
Рассмотрим качественную картину движения газа перед поршнем (при любом законе движения поршня). Подставим значение константы во второе уравнение системы (3.47)
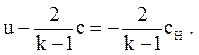 (3.50)
(3.50)
С другой стороны, мы имеем в простой волне (3.45)
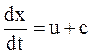
Исключим с из этого выражения. Для этого выразим с из уравнения (3.50)
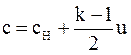
и подставим в уравнение
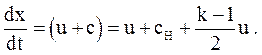 (3.51)
(3.51)
Скорость поршня uн известна (предполагаем, что известен закон движения поршня), поэтому можем написать
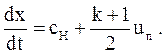 (3.52)
(3.52)
Таким образом, любое состояние газа, которое возникает у поршня, передвигается по газу со скоростью 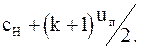 Определим наклон характеристик в плоскости x, t для некоторых фиксированных положений поршня:
Определим наклон характеристик в плоскости x, t для некоторых фиксированных положений поршня:
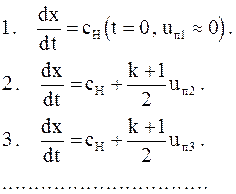 (3.53)
(3.53)
Наклон характеристик 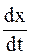 с увеличением скорости поршня постепенно увеличивается, а величина с увеличением скорости поршня постепенно увеличивается, а величина 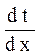 уменьшается (рис. 3.8).
С физической точки зрения это объясняется тем, что каждая уменьшается (рис. 3.8).
С физической точки зрения это объясняется тем, что каждая
| 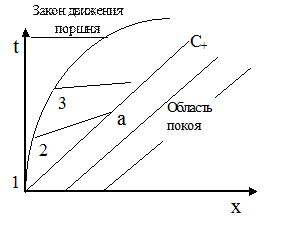 Рис. 3.8. Семейство характеристик.
Рис. 3.8. Семейство характеристик.
|
последующая элементарная волна сжатия движется по газу, более уплотненному предыдущей волной, и амплитуда волны непрерывно увеличивается. Характеристики в конце концов пересекаются в какой-то точке (см. рис. 3.8). Поскольку вдоль каждой характеристики в плоскости x, t для простой волны параметры среды u и c постоянны, то в точке пересечения характеристик (точка а на рис. 3.8) нарушается однозначность параметров среды. В точке пересечения характеристик возникает ударная волна (все параметры газа изменяются скачком) и течение становится неизоэнтропическим (в этом случае необходимо использовать адиабатические уравнения движения среды).
Уравнения (3.47) описывают движение газа в трубе только до момента образования ударной волны.
Проведенный выше анализ, следовательно, показывает, что в случае ускоренного движения поршня из волны сжатия формируется ударная волна.
Определим теперь функцию F(u). Для этого мы должны задать закон движения поршня.
Задача 1. Пусть в нашем случае поршень движется равноускоренно. Закон движения поршня описывается уравнениями (а - ускорение)
|
|
|
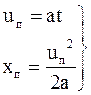 (3.54)
(3.54)
Выразим функцию F(u) из первого уравнения (3.47)
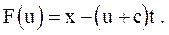
Подставим в это уравнение выражения для xп и t из (3.54) с учетом, что 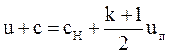 , и получим выражение для функции F(u):
, и получим выражение для функции F(u):
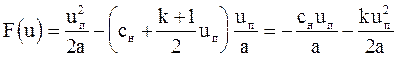 (3.55)
(3.55)
Теперь мы можем записать решение (3.47) нашей задачи в окончательном виде:
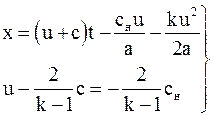 (3.56)
(3.56)
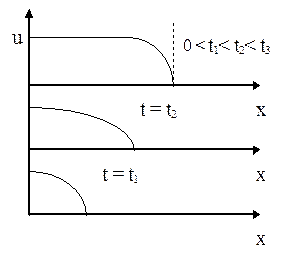 Рис. 3.9. Распределение скоростей. Рис. 3.9. Распределение скоростей.
| На рис. 3.9 показана зависимость u=u(x) для разных моментов времени t.
Определим давление и плотность в волне сжатия. Так как газ совершенный, то есть 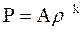 , то соотношение, связывающее параметры газа перед волной сжатия и в , то соотношение, связывающее параметры газа перед волной сжатия и в
|
самой волне, записывается для скоростей звука и плотностей в виде
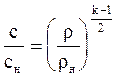 (3.57)
(3.57)
или для давлений, плотностей и скоростей звука
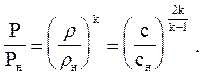 (3.58)
(3.58)
Поскольку закон изменения c = c(x, t) известен из уравнений (3.56), то соотношения (3.58) позволяют определить Р = Р(x, t) и r = r (x, t).
Теперь определим момент и координату образования ударной волны. В момент образования ударной волны производная скорости по координате x стремится к бесконечности, (см. рис. 3.9), то есть
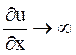 или
или 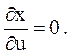 (3.59)
(3.59)
Найдем эту производную и приравняем ее к нулю. Уравнение (3.56) с учетом, что 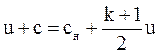 , можно записать в виде
, можно записать в виде
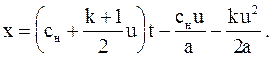 (3.60)
(3.60)
Продифференцируем это выражение по u и приравняем его к нулю:
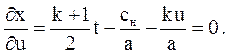 (3.61)
(3.61)
Выразим из этого уравнения время, которое и будет моментом образования ударной волны
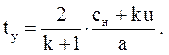 (3.62)
(3.62)
Минимальное время образования ударной волны соответствует u = 0. В этот момент времени пересекутся две первые характеристики (см. т. а на рис. 3.8) при u = 0 и образуется ударная волна
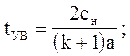 (3.63)
(3.63)
Координата образования ударной волны
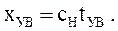 (3.64)
(3.64)
Следует отметить, что с момента образования ударной волны перестают быть справедливыми уравнения, описывающие изоэнтропические, описывающие движение движения, так как после возникновения ударной волны энтропия каждой частицы среды изменится.
Поэтому уравнения волны сжатия, справедливы для времени t £ tУВ , тогда x £ xУВ.
В случае, если поршень мгновенно приобретает скорость, то есть a ® ¥, то ударная волна возникает в момент времени tУВ= 0 и xУВ= 0.
3.7. Волны разрежения. разлет продуктов детонации в пустоту
Рассмотрим теперь движение газа под действием поршня, выдвигающегося из трубы. Пусть покоящийся газ с постоянной плотностью, давлением и скоростью звука rн, Pн, cн занимает пространство в жесткой трубе справа от поршня (x > 0). В момент t = 0 поршень начинает двигаться влево, постепенно ускоряясь от нулевой скорости до некоторой постоянной скорости. Вправо от поршня возникает волна разрежения (рис. 3.10).
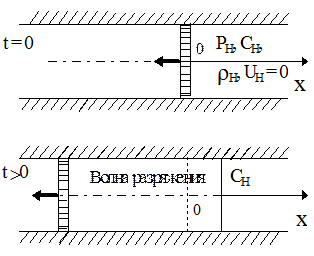 Рис. 3.10. Расчетная схема. Рис. 3.10. Расчетная схема.
| Эта волна разрежения является простой римановской волной, так как зона, охваченная волной, граничит с зоной покоя. Волна разрежения описывается особым решением
 (3.65) (3.65)
|
поскольку она движется в положительном направлении оси ox, хотя направление массовой скорости газа при этом противоположно. Определим значение константы в системе (3.65). Для этого воспользуемся граничными условиями на фронте волны разрежения:
u = 0, c = cн.
Тогда получим
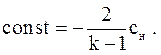 (3.66)
(3.66)
Затем из второго уравнения (3.65) получим для скорости звука
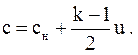 (3.67)
(3.67)
Дифференциальное выражение для характеристики в плоскости x, t имеет вид
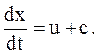
Подставим в это выражение значение (3.67) и получим
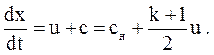 (3.68)
(3.68)
На границе с поршнем скорость газа совпадает со скоростью поршня uп, направление которой отрицательно относительно оси x. Скорость звука, а также давление и плотность газа у поршня меньше начальных, притом тем меньше, чем скорее движется поршень. Характеристики C+ являются прямыми линиями, выходят с линии поршня (возмущения возникают на поршне) и имеют наклоны
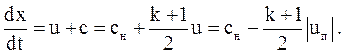 (3.69)
(3.69)
На рис. 3.11 показаны характеристики C+ в плоскости x, t. В области I между осью ox и oA — характеристикой C+ газ невозмущен и характеристики представляют собой параллельные линии. Первое возмущение от поршня распространяется по газу со скоростью cн и поэтому закон движения начального возмущения имеет вид x = cнt.
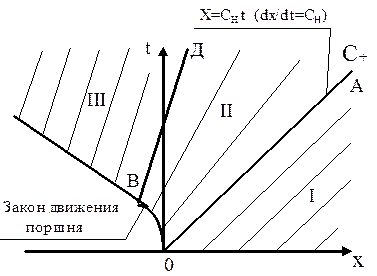
Рис. 3.11. Семейство характеристик.
Далее движение поршня постепенно ускоряется (зона II на рис. 3.11) и характеристики C+ расходятся. Это объясняется тем, что каждое следующее возмущение идет по газу, уже разреженному предыдущим возмущением. Характеристики C+, выходящие с того участка линии поршня, на котором скорость поршня уже постоянна (область III), имеют одинаковые наклоны и идут параллельно друг другу.
Задача. В том случае, когда поршень мгновенно приобретает какую-то конечную скорость V0, образуется центрированная волна разрежения.
| Центрированная волна разрежения представляет собой предельный случай, когда время переменного движения поршня стремится к нулю (рис. 3.12). Характеристики C+, соответствующие началу движения поршня, вы- |  Рис. 3.12. Центрированная волна разряжения. Рис. 3.12. Центрированная волна разряжения.
|
ходят из одной точки O (характеристики ОА и ОД на рис. 3.12).
Такой центрированной волне разрежения отвечает решение, соответствующее F(u) = 0:
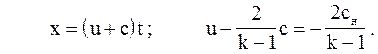
Отсюда определяется скорость частиц в волне разрежения
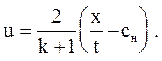
Характеристики С+ имеют вид
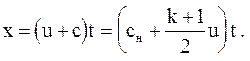
Каждому ui = const соответствует своя линия С+ в плоскости x, t (см. рис. 3.12); так, вдоль линии ОА: uA= 0 и линии ОД: uД = -V0 (скорость поршня).
Поскольку 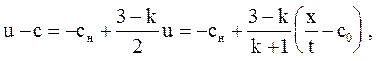 то уравнение характеристик С_, при
то уравнение характеристик С_, при 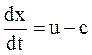 , имеет вид
, имеет вид
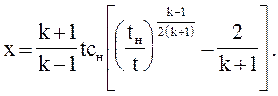
Начальные координаты xн, tн характеристики С_ лежат на линии xн=cн tн.
Траектории частиц (характеристики С0) определяются с помощью уравнения 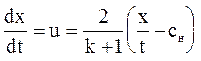 , отсюда после интегрирования получим
, отсюда после интегрирования получим
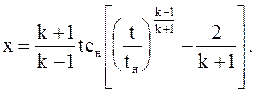
На рис. 3.12 показано семейство С+ и по одной из характеристик С_ и С0.
Представляется интересным выяснить, с какой скоростью должен двигаться поршень, чтобы оторваться от газа. Это равносильно тому случаю, когда поршень мгновенно убирается и газ начинает истекать в пустоту.
Инвариант Римана в этом случае, как и в случае волны разрежения, рассмотренного выше, будет равен
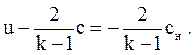
Поскольку в пустоте скорость звука c = 0 (так как r = 0, а c ~ r (k-1)/ 2), то скорость истечения будет равна
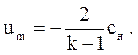 (3.70)
(3.70)
Следовательно, если поршень будет иметь скорость
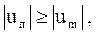 (3.71)
(3.71)
то он оторвется от газа и газ будет свободно истекать в пустоту.
Задача. Одностороннее истечение ранее покоящегося газа в пустоту.
Представим себе очень длинную трубу, перегороженную где-то в середине перегородкой. Пусть область слева от перегородки заполнена покоящимся газом с параметрами Pн, r н , cн , uн = 0, а справа от перегородки — пустота. Ось ox направим параллельно оси трубы, начало координат пусть будет в том месте, где находится перегородка. Площадь сечения трубы постоянна и принимается равной единице (рис. 3.13).
| Теперь мгновенно уберем перегородку в момент времени t=0. Сразу же газ начнет истекать в пустоту, и одновременно с этим возникнет волна разрежения, бегущая влево. Истечение газа в пустоту является неустановившимся, а волна разрежения - простой (риманов-ской) волной, она представляет | 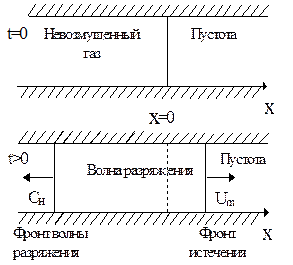 Рис. 3.13. Расчетная схема. Рис. 3.13. Расчетная схема.
|
собой волну одного направления, распространяющуюся по невозмущенному газу, то есть область нестационарного течения газа граничит с областью покоя.
Следует отметить, что движущаяся вправо граница разлета не является волной, так как там частицы газа, сами двигаясь, не приводят в движение никакую среду. Распределение скорости и плотности газа по обе стороны от снятой стенки описываются одними и теми же уравнениями.
Ввиду того, что данная волна разрежения является простой волной, для решения этой задачи воспользуемся уравнениями:
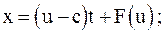 (3.72)
(3.72)
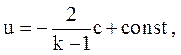 (3.73)
(3.73)
так как возмущения распространяются в отрицательном направлении оси x.
Значение неизвестных F(u) и const будем искать с помощью граничных условий. Очевидно, что для покоящегося газа (на фронте волны) u = 0 и c = cн. Подставим это условие в уравнение (3.73) и получим 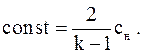 (3.74)
(3.74)
Тогда уравнение (3.73) окончательно примет вид
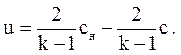 (3.75)
(3.75)
Из этого уравнения видно, что максимальная предельная скорость истечения в пустоту (при c=0)
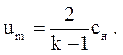 (3.76)
(3.76)
Значение неизвестной F(u) определим из второго условия, которое состоит в том, что в начальный момент, когда мгновенно убирается перегородка (t = 0), значения u и c в месте нахождения перегородки (x = 0) являются неопределенными. Действительно, в начальный момент при снятии перегородки u и c не имеют определенных значений, так как скорость u скачком возрастает от нуля до своего предельного значения um, определяемого уравнением (3.76), а плотность, давление и скорость звука скачком падают до нуля от своих первоначальных значений r н, Pн и cн.
Покажем, что при этих условиях F(u) должна тождественно равняться нулю. Так как движение газа в начальный момент t = 0 определено в сечении x = 0, то F(u) должно быть равно нулю. В этом случае
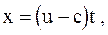 (3.77)
(3.77)
отсюда при t = 0 и x = 0 получаем
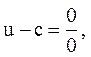
то есть u и c являются произвольными (неопределенными), что и соответствует условиям нашей задачи.
Итак, решение окончательно запишется в виде
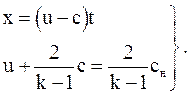 (3.78)
(3.78)
Определим теперь закон движения фронта волны разрежения. Этот фронт в каждый данный момент граничит с областью невозмущенного газа в трубе, поэтому на фронте u = 0 и c = cн. Следовательно, для фронта волны разрежения первое уравнение (3.78) дает
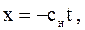 (3.79)
(3.79)
то есть фронт волны движется справа налево со скоростью cн, равной местной скорости звука. Само соотношение (3.79) является характеристикой наших уравнений.
Из полученного решения (3.78) видно, что рассматриваемое движение газа можно характеризовать одной переменной 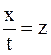 . Такое движение называется автомодельным.
. Такое движение называется автомодельным.
Покажем, что все параметры, характеризующие данное движение, являются функциями одной переменной 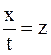
 . Для этого запишем уравнения (3.78) в виде:
. Для этого запишем уравнения (3.78) в виде:
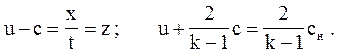
Найдем зависимость скорости газа u и скорости звука с от переменной 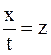 :
:
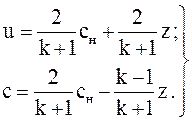 (3.80)
(3.80)
| Из уравнений (3.80) видно, что в каждый данный момент u и c являются линейными функциями от x (рис. 3.14). Далее из уравнений (3.80) следует, что в сечении x = 0 всегда | 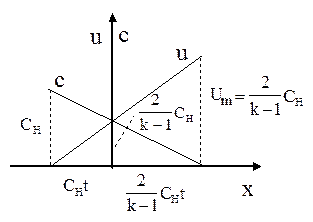 Рис. 3.14. Распределение скоростей.
Рис. 3.14. Распределение скоростей.
|
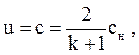 (3.81)
(3.81)
то есть устанавливается критический режим истечения. Очевидно, что состояние, при котором u = c, не перемещается по газу, так как скорость распространения состояния u - c в этом случае равна нулю.
Для данной задачи в плоскости u, c (рис.3.15) имеется одна характеристика
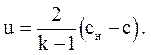 (3.82)
Каждой i-й точке этой характеристики (ui; ci) соответствует прямая (3.82)
Каждой i-й точке этой характеристики (ui; ci) соответствует прямая
| 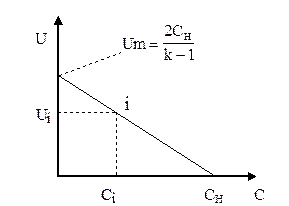 Рис. 3.15. Распределение скоростей
Рис. 3.15. Распределение скоростей
|
характеристика С_ в плоскости x, t
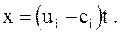
Все эти характеристики проходят через начало координат (x = 0, t = 0) и отличаются друг от друга угловым коэффициентом (ui - ci). Такая простая волна называется центрированной волной (рис. 3.16).
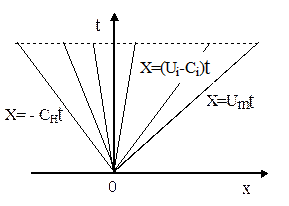 Рис. 3.16. Центрированная волна разряжения
Рис. 3.16. Центрированная волна разряжения
|
Область разлета газа в плоскости (x, t) ограничена фронтом разлета в пустоте 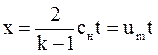 , а слева - фронтом волны разрежения x = - CH t. Критическому ре- , а слева - фронтом волны разрежения x = - CH t. Критическому ре-
|
жиму истечения ui = ci соответствует характеристика x = 0 (рис. 3.16).
 2015-09-06
2015-09-06 872
872








