2015-10-22
1352
Если дано линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами
,
правая часть которого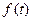 
является оригиналом, то и решение этого уравнения, удовлетворяющее произвольным начальным условиям вида 
, 
, …, 
(т.е. решение задачи Коши, поставленной для этого уравнения, с начальными условиями при 
), служит оригиналом. Обозначая изображение этого решения через 
, находим изображение левой части исходного дифференциального уравнения и, приравнивая его изображению функции 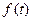, приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно . Определив из этого уравнения , находим оригинал 
.
Тот же метод перехода к изображающему уравнению позволяет легко найти решение интегральных уравнений вида
, 
,
В которых функции 
и 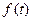являются оригиналами, поскольку входящий в эти уравнения интеграл является сверткой функций и .
Эти интегральные уравнения являются частным случаем интегральных уравнений Вольтера первого и второго рода, общий вид которых получается, если заменить функцию 
(ее называют ядром интегрального уравнения) некоторой функцией двух аргументов 
.
|
|
|
Решение примеров
Пример 1. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 5 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут 2 женщины и 3 мужчины.
Решение: Число всех способов выбора 5 человек из 25 равно 
,а число способов выбора двух женщин из 5 равно 
. Каждая такая двойка может сочетаться с каждой тройкой из 20 мужчин. Число таких троек равно 
. Искомая вероятность составляет
Р= 
= 
.
Пример 2. Слово «лотос», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово «сто»?
Решение: Вероятность появления буквы «с» равна 1/5. Вероятность появления вслед за ней буквы «т» равна 1/4, и, наконец, вероятность появления буквы «о» равна 2/3.
Искомая вероятность Р = 
= 
33.
Пример 3. Случайно встреченное лицо с вероятностью 0,2может оказаться брюнетом, с вероятностью 0,3 — блондином, с вероятностью 0,4 — шатеном и с вероятностью 0,1 — рыжим. Каковая вероятность того, что среди пяти случайно встреченных лиц: а) не менее четырех блондинов; б) два блондина и три шатена; в) хотя бы один рыжий?
Решение:
а) Искомая вероятность составляет [см. формулу (1)]
P=P5(4)+P5(5)= 
=0,03078.
б) Искомая вероятность P=P5(2) 
P5(3)= 
,07.
в) Искомая вероятность P=1-P5(0)=1- 
=1-0,6561=0,3439.
Пример 4. Игральную кость подбрасывают 500 раз. Какова вероятность того, что шестерка при этом выпадет 50 раз?
|
|
|
Решение: Здесь n = 500; k = 50; р = 1/6; q = 5/6; 
x= 
По формуле (2) находим искомую вероятность:
P500(50)= 
Пример 5. Пусть вероятность того, что покупателю необходимо купить обувь 41-го размера, равна 0,2. Найти вероятность того, что из 400 покупателей не более 100 потребуют обувь этого размера.
Решение: По условию, n=400; p= 0,2; q=0,8; k1=0; k2=100; 
x1= 
Согласно формуле (3), искомая вероятность есть
P400(0;400)=Ф(2,5)- Ф(-10)= Ф(2,5)+ Ф(10)=0,49379+0,5=0,99379.
Пример 6. Непрерывная случайная величина X распределена нормально. Известно, что D(х)=4 и Р(х<1) = 0,5. Найти Р(х>0).
Решение: По формуле (4) получим Р(х>0)= Р(0<х<+ 
)= Ф( 
)- Ф( 
)= Ф ( 
)- Ф( 
).
Найдем а. Имеем Р(х<1)=Р(- <х<0)= Ф( 
)- Ф(- 
)= Ф( )+0,5
откуда Ф( )+0,5=0,5=> Ф( )=0,5 => 
=>a=1
Окончательно находим Р(х>0)= Ф ( )- Ф( )=0,5+Ф ( 
)=0,5+0191462=0,691462.
Пример 7. Дифференцируема ли функция 
?
Находим 
, 
, 
, 
, 
, 
. Одно из условий Коши-Римана не выполняется. Таким образом, данная функция не является дифференцируемой.
Пример 8. Дифференцируема ли функция 
?
Имеем 
, 
; 
, 
, 
, 
; 
, 
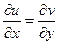. Условия Коши-Римана выполняются. Следовательно, функция дифференцируема. Так как 
, то
.
Производную 
можно найти и иначе:
, 
.
Пример 9. Является ли дифференцируемой функция 
?
Находим 
, 
; 
, 
, 
, 
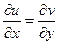; , . Условия Коши-Римана выполнены. Далее, имеем
, или иначе
, 
.
Пример 10. 
; 
Пример 11. Решить дифференциальное уравнение 
, если 
, 
.
Переходим к изображениям:
,
или
; 
.
Разложим эту рациональную дробь на простейшие дроби:
,
.
Полагая 
, получаем 
, т.е. 
; при 
имеем 
, т.е. 
. Сравнивая коэффициенты при 
, получим 
, т.е. 
. Следовательно,
,
откуда
.
Пример 12. Решить уравнение 
, если , 
.
Переходим к изображениям:
.
После несложных преобразований получим
.
Отсюда 
.
Пример 13. Решить систему уравнений.
,
Если 
, 
.
Перейдя к изображениям, имеем
Решив эту систему относительно 
и 
, получаем
, 
.
Для определения 
воспользуемся второй теоремой разложения и формулой:
, 
, 
,
, 
, 
;
, 
, 
.
Таким образом, 
. Аналогично находим 
.
