Число – абстракция, используемая для количественной характеристики объектов. Письменными знаками – символами для записи чисел служат цифры.
В математике выделяют натуральные числа 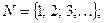 целые числа
целые числа 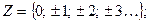 (кстати, слово нуль означало отсутствие числа и буквальный смысл латинского слова nullum – «ничто»); рациональные числа
(кстати, слово нуль означало отсутствие числа и буквальный смысл латинского слова nullum – «ничто»); рациональные числа 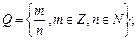 иррациональные числа
иррациональные числа 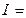 {бесконечная непериодическая десятичная дробь}; действительные числа
{бесконечная непериодическая десятичная дробь}; действительные числа 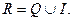 Очевидно, что
Очевидно, что 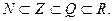
Множество действительных чисел R дополняют символом бесконечности 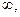 который не является числом. Он представляет собой символическое обозначение безграничного удаления числа от начала координат. При этом полагают, что
который не является числом. Он представляет собой символическое обозначение безграничного удаления числа от начала координат. При этом полагают, что
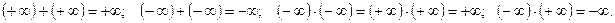
Но операции 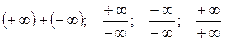 не определены.
не определены.
В современной математике помимо действительных чисел используются комплексные числа. Они возникли в связи с решением алгебраических уравнений третьей степени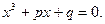 Формула для нахождения корней кубического уравнения, открытая Д. Карадано и Р. Бомбелли в XVI веке имела вид:
Формула для нахождения корней кубического уравнения, открытая Д. Карадано и Р. Бомбелли в XVI веке имела вид:
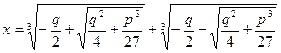 ).
).
Пример 1. Найти размер куба, объем которого на шесть единиц меньше суммы семи его ребер.
Решение. Пусть x – сторона куба; x 3 – объем куба; 7 x – сумма семи его ребер. Из условия задачи имеем: 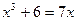 или
или 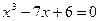 . Решим данное уравнение двумя способами:
. Решим данное уравнение двумя способами:
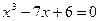
| |
| 1 способ: | 2 способ: |
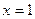 – корень уравнения (подбор);
Уравнение может быть представлено – корень уравнения (подбор);
Уравнение может быть представлено 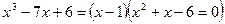 .
Решением данного уравнения являются числа: .
Решением данного уравнения являются числа: 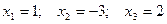 Таким, образом, куб с описанным свойством существует.
Таким, образом, куб с описанным свойством существует.
| Используем формулу для корней кубического уравнения при 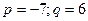 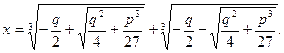
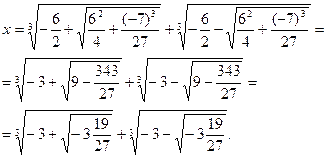 Под знаком квадратного корня оказалось отрицательное число. Получается, что путь к корням идет через невозможную операцию извлечения квадратного корня из отрицательного числа
Под знаком квадратного корня оказалось отрицательное число. Получается, что путь к корням идет через невозможную операцию извлечения квадратного корня из отрицательного числа
|
Так как задача имеет реальное решение, то появляется необходимость определить корень из отрицательного числа, а именно определить величину 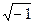 . Новые числа, для которых определили величину
. Новые числа, для которых определили величину 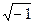 , назвали комплексными. Комплексные числа появились в XVI веке при решении уравнений третьей степени, когда стало ясно, что реальные решения уравнений существуют, но не могут быть найдены действиями над действительными числами.
, назвали комплексными. Комплексные числа появились в XVI веке при решении уравнений третьей степени, когда стало ясно, что реальные решения уравнений существуют, но не могут быть найдены действиями над действительными числами.
Понятие комплексного числа, его алгебраическая форма
Комплексным числом z называется выражение вида 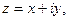 где x и y – действительные числа, а i – мнимая единица,
где x и y – действительные числа, а i – мнимая единица, 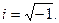
Число x называется действительной частью комплексного числа z и обозначается 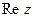 (от французского reele – действительный), а число y – мнимой частью комплексного числа z и обозначается
(от французского reele – действительный), а число y – мнимой частью комплексного числа z и обозначается 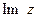 (от французского imaginaire – мнимый).
(от французского imaginaire – мнимый).
Если 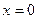 , то число
, то число 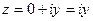 называется чисто мнимым; если
называется чисто мнимым; если 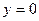 , то число
, то число 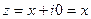 превращается в действительное число. Множество всех комплексных чисел обозначается C. Из вышесказанного ясно, что множество всех действительных чисел является подмножеством комплексных чисел, т.е.
превращается в действительное число. Множество всех комплексных чисел обозначается C. Из вышесказанного ясно, что множество всех действительных чисел является подмножеством комплексных чисел, т.е. 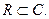
Два комплексных числа 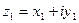 и
и 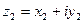 называются равными, если
называются равными, если 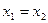 и
и 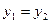 . Понятие «больше» и «меньше» для комплексных чисел не вводят.
. Понятие «больше» и «меньше» для комплексных чисел не вводят.
Два комплексных числа 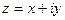 и
и 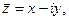 отличающиеся лишь знаком мнимой части, называются сопряженными.
отличающиеся лишь знаком мнимой части, называются сопряженными.
Выражение 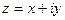 называют алгебраической формой комплексного числа.
называют алгебраической формой комплексного числа.
Арифметические действия над комплексными числами
в алгебраической форме
1. Сложение комплексных чисел
Суммой двух комплексных чисел 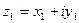 и
и 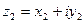 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 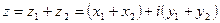 .
.
2. Вычитание комплексных чисел
Разностью двух комплексных чисел 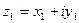 и
и 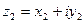 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 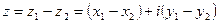 .
.
Теорема 1. Сумма двух сопряженных комплексных чисел является действительным числом, а разность – чисто мнимым.
□ 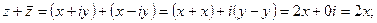
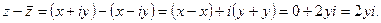 ■
■
3. Умножение комплексных чисел
Произведением двух комплексных чисел 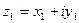 и
и 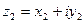 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
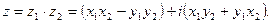
Эту формулу можно получить, перемножая комплексные числа, как многочлены с учетом 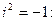
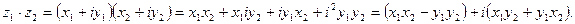
Теорема 2. Произведение двух сопряженных комплексных чисел является действительным числом, равным сумме квадратов действительной и мнимой частей.
□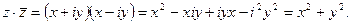 ■
■
4. Деление комплексных чисел
Частным двух комплексных чисел 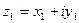 и
и 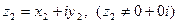 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
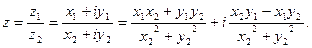
Данная формула может быть получена домножением числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»): 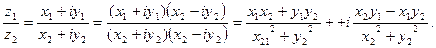
Пример 2. Даны 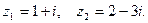 Найти:
Найти: 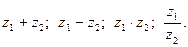
Решение: 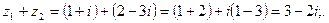
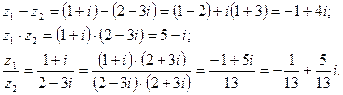
Тригонометрическая форма комплексного числа
Всякое комплексное число можно изобразить на плоскости. Плоскость, на которой изображаются комплексные числа, называется комплексной. Ось абсцисс называется действительной осью, а ось ординат – мнимой осью.
Комплексное число 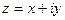 можно задать с помощью радиус-вектора
можно задать с помощью радиус-вектора 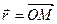 , начало которого в точке
, начало которого в точке 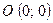 , а конец в точке
, а конец в точке 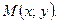
Длина вектора 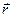 называется модулем комплексного числа и обозначается
называется модулем комплексного числа и обозначается 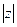 или
или 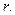 Величина угла между положительным направлением действительной оси и вектором
Величина угла между положительным направлением действительной оси и вектором 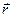 называется аргументом этого комплексного числа и обозначается
называется аргументом этого комплексного числа и обозначается 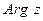 или
или 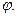 Аргумент комплексного числа величина многозначная и определяется с точностью до
Аргумент комплексного числа величина многозначная и определяется с точностью до 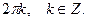 Значение аргумента, заключенное в промежутке
Значение аргумента, заключенное в промежутке  (
(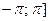 , обозначается
, обозначается 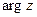 и называется главным значением аргумента. Очевидно, что
и называется главным значением аргумента. Очевидно, что 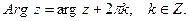
 Определим еще одну форму записи комплексного числа – тригонометрическую. Её легко получит из геометрической интерпретации комплексного числа (рис.1).
Определим еще одну форму записи комплексного числа – тригонометрическую. Её легко получит из геометрической интерпретации комплексного числа (рис.1).
Из прямоугольного треугольника получаем 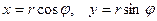 . Подставляя найденные выражения x и y в алгебраическую форму комплексного числа
. Подставляя найденные выражения x и y в алгебраическую форму комплексного числа 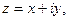 получим
получим 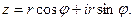
Рис.1
Тригонометрической формой комплексного числа называется запись
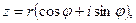
где r –модуль комплексного числа, определяемый по формуле 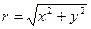 , а
, а 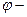 его аргумент, определяемый из формул
его аргумент, определяемый из формул 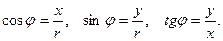
При переводе комплексного числа из алгебраической формы в тригонометрическую, в качестве аргумента берут только главное значение, то есть считают 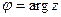 . Такое допущение следует из того, что функция синуса и косинуса имеют период
. Такое допущение следует из того, что функция синуса и косинуса имеют период 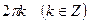 и поэтому:
и поэтому:
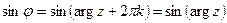 и
и 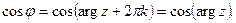
Пример 3. Записать комплексные числа 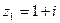 ;
; 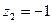 и
и 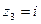 в тригонометрической форме.
в тригонометрической форме.
Решение. Для 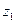 имеем
имеем 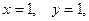
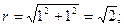
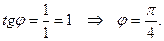 Отсюда
Отсюда 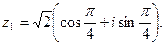
Для 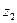 имеем
имеем 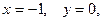
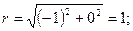
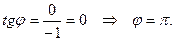 Отсюда
Отсюда 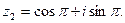
Для 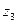 имеем
имеем 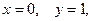
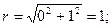
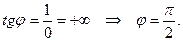 Отсюда
Отсюда 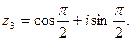
Арифметические действия над комплексными числами
в тригонометрической форме
1. Умножение комплексных чисел
Произведением комплексных чисел 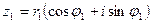 и
и 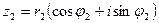 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
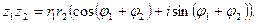
Формула получена следующим образом:
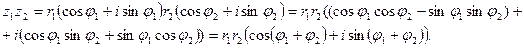
Таким образом, при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей.
2. Возведение комплексных чисел в натуральную степень
Для возведения комплексного числа в натуральную степень нужно возвести в эту степень модуль этого числа, а аргумент умножить на показатель степени.
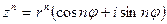 .
.
Эта формула называется формулой Муавра. Формула была получена английским математиком Абрахамом де Муавром (1667–1754) в 1707 г., а современная её запись предложена Леонардом Эйлером в 1748 г.
3. Деление комплексных чисел
Частным двух комплексных чисел 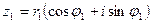 и
и 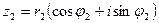 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
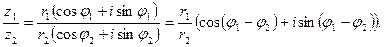
Таким образом, при делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.
4. Извлечение корня из комплексного числа
Корнем n -й степени из комплексного числа 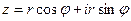 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
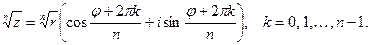
Пример 4. Найти значения: а)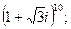 б)
б) 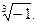
Решение. а) Запишем число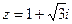 в тригонометрической форме:
в тригонометрической форме:
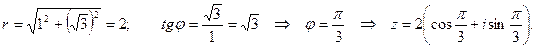
По формуле Муавра имеем
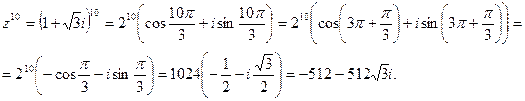
б) Запишем подкоренное число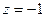 в тригонометрической форме:
в тригонометрической форме: 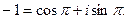 Поэтому,
Поэтому, 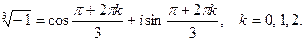 При
При 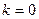 получаем
получаем 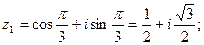 при
при 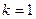 получаем
получаем 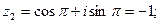 при
при 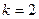 получаем
получаем 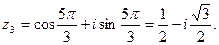
Таким образом, 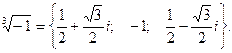
 2014-01-25
2014-01-25 1423
1423








