ТЕМА 2 Отбор факторов при построении множественной регрессии

В экономической практике часто имеет место сложная, многопричинная статистическая связь между признаками. В таком случае зависимость y=f(x) означает, что х – вектор, содержащий m компонентов х=(х₁, х₂, …, х_m) формулируется аналогично случаю парной регрессии. Записывается функция y=f(a,x)+ε, где а – вектор параметров, ε – случайная ошибка. Предполагается, что эта функция связывает переменную y с вектором независимых переменных х для данной генеральной совокупности. Как и в случае парной регрессии, предполагается, что ошибки ε_i являются случайными величинами с нулевым математическим ожиданием и постоянной дисперсией; ε_i и ε_j статистически независимые при ij. Кроме того, для проверки статистической значимости оценок а обычно предполагается, что ошибки ε_i нормально распределены. По данным наблюдений выборки размерности n требуется оценить значения параметров а.

Чтобы формально можно было решить задачу, должно быть . Если число степеней свободы мало, то статистическая надежность оцениваемой формулы невысока. Обычно при оценке множественной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений по крайней мере в три раза превосходило число оцениваемых параметров.

Для оценивания параметров применяется, как правило, метод наименьших квадратов. Уравнение регрессии с оцененными параметрами имеет вид:

                                                         (2.1)

 

И критерием для нахождения вектора а является ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

 

 

Приравнивая нулю частные производные по каждому параметру, составляем систему нормальных уравнений относительно неизвестных параметров а_i:

Например, приравняем производные по параметру а₁:

Система нормальных уравнений с m неизвестными (по числу параметров а_i) имеет вид:

 

Для двухфакторной модели данная система будет иметь вид:

Так же можно воспользоваться готовыми формулами, которые являются следствием из этой системы:

 

 

 

В линейной множественной регрессии параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

       Одним из способов построения множественных уравнений регрессии является построение модели связи в стандартизированном масштабе.

       Оценка влияния каждого факторного признака, включенного в уравнение регрессии, на результативный признак может быть затруднена, если факторные признаки различны по своей сущности и имеют различные единицы измерения В этих случаях для более точной оцеки влияния факторных признаков используют множественные модели регрессии в стандартизованном масштабе. Модель регрессии в стандартизованном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты по формуле:

 

где х_i – значение признака в натуральном масштабе.

 

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе

 

где t_y, - стандартизированные переменные: , , для которых среднее значение равно нулю =0, а среднее квадратическое отклонение равно единице:

В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии β_i можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой. Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

где - коэффициенты парной и межфакторной корреляции.

 

Коэффициенты «чистой» регрессии b_i связаны со стандартизованным коэффициентами регрессии следующим образом:

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1) при этом параметр a определяется как

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением β _i.

       Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

При линейной зависимости коэффициент множественной корреляции можно определить через матрицы парных коэффициентов корреляции:

где:

– определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

Так же при линейной зависимости признаков формула коэффициента множественной корреляции может быть также представлена следующим выражением:

Где β_i – стандартизованные коэффициенты регрессии; r_yxi – парные коэффициенты корреляции результата с каждым фактором.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции

Для того чтобы не допустить преувеличения тесноты связи, применяется скорректированный индекс множественной детерминации, который содержит поправку на число степеней свободы и рассчитывается по формуле.

 

где n – число наблюдений, m – число факторов. При небольшом числе наблюдений нескорректированная величина коэффициента множественной детерминации R 2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на y фактора x_i, при элиминировании (исключении влияния) других факторов, можно определить по формуле

 

 

или по рекуррентной формуле:

 

Формула 2.13.

 

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде.

При двух факторах формулы (2.11) и (2.12) примут вид:

 

 

 

Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера:

 

 

Частный F -критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора x частный F -критерий определится как

 

 

Фактическое значение частного F -критерия сравнивается с табличным при уровне значимости a и числе степеней свободы: k₁ =1 и k₂ = n - m -1. Если фактическое значение  F_xi превышает F_табл (а, к₁, к₂) то дополнительное включение фактора x_i в модель статистически оправданно и коэффициент чистой регрессии b_i при факторе x_i статистически значим.

Если же фактическое значение F_xi меньше табличного, то дополнительное включение в модель фактора x_i не увеличивает существенно долю объясненной вариации признака y, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

Оценка значимости коэффициентов чистой регрессии проводится по t -критерию Стьюдента. В этом случае, как и в парной регрессии, для каждого фактора используется формула

 

Для уравнения множественной регрессии (2.1) средняя квадратическая ошибка коэффициента регрессии может быть определена по формуле:

 

 

где  - коэффициент детерминации для зависимости фактора x_i совсеми другими факторами уравнения множественной регрессии. Для двухфакторной модели (m = 2) имеем:

 

 

Существует связь между t -критерием Стьюдента и частным F -критерием Фишера:

 

Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т.д.). Чтобы ввести такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т.е. качественные переменные преобразовать в количественные.

Такого вида сконструированные переменные принято в эконометрике называть фиктивными переменными. Например, включать в модель фактор «пол» в виде фиктивной переменной можно в следующем виде:

 

 

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории (женский пол) к другой (мужской пол) при неизменных значениях остальных параметров.

 

 

Вопрос 2: «F-тест на качество оценивания».

Для определения статистической значимости коэффициента детерминации проверяется нулевая гипотеза для F-статистики, рассчитываемой по формуле

 

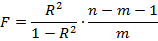
Соответственно для парной регрессии

 

 

Смысл проверяемой гипотезы заключается в том, что все коэффициенты линейной регрессии, за исключением свободного параметра, равны нулю (случай отсутствия линейной функциональной связи). Если они действительно равны нулю для генеральной совокупности, то уравнение регрессии должно иметь вид  , а коэффициент детерминации и F-статистика Фишера также равны нулю. При этом их оценки для случайной выборки, конечно, отличаются от нуля, но чем больше такое отличие, тем менее оно вероятно. Логика проверки нулевой гипотезы заключается в том, что если произошло событие, которое было бы слишком маловероятным в том случае, если данная гипотеза действительно была бы верна, то эта гипотеза отвергается.

Величина F имеет распределение Фишера с (m, n-m-1) степенями свободы, где m – число объясняющих переменных, n – число наблюдений. Распределение Фишера – двухпараметрическое распределение неотрицательной случайной величины, являющейся в частном случае при m=1 квадратом случайной величины, распределенной по Стьюденту. Для распределения Фишера имеются таблицы критических значений, зависящих от числа степеней свободы m и n-m-1 при различных уровнях значимости.

Для проверки гипотезы при заданном уровне значимости по таблицам находится критическое значение F_крит, и нулевая гипотеза отвергается, если F>F_крит. Например, при оценке парной регрессии по 15 наблюдениям R²=0,7. В этом случае F=0,7*13:0,3=30,3. По таблицам для распределения Фишера с (1;13) степенями свободы найдем, что при 5%-ном уровне значимости (доверительная вероятность 95%) критическое значение F равно 4,67, при 1%-ном 9,07. Поскольку F=30,3>F_крит, нулевая гипотеза в обоих случаях отвергается, т.е. отвергается предположение о незначимости связи.

В случае парной регрессии проверка нулевой гипотезы для t-статистики коэффициента регрессии равносильно проверка нулевой гипотезы F-статистики (и соответственно R²). В этом случае F-статистика равна квадрату t-статистики. В случае парной регрессии статистическая значимость величин R² и t-статистики коэффициента регрессии определяется коррелированностью переменных х и у. Самостоятельную важность показатель R² приобретает в случае множественной линейной регрессии.

Распределение Фишера может быть использовать не только для проверки гипотезы об одновременно равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части эти коэффициентов. Это особенно важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных или, наоборот, включения их в это число.

При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты:

1. Построенная модель на основе ее проверки F-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов.

2. Модель по F-критерию адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для получения прогнозов.

3. Модель по F-критерию Фишера адекватна, но все коэффициенты регрессии незначимы. В этом случае модель полностью считается неадекватной. На её основе не принимаются решения и не осуществляются прогнозы.