Площадь криволинейной трапеции

Применение интегралов

К решению прикладных задач

Выполнил студент

Группы 3-М-2

Ширшов Вадим Алексеевич

Проверила

Воробьёва Н.Г.

Орехово-Зуево.

2008

 

Содержание

 

Вступление.

1. Определённый интеграл.

1.1 Площадь криволинейной трапеции.

1.2 Объём тела.

1.3 Длина дуги.

1.4 Площадь поверхности вращения.

1.5 Нахождение статического момента и центра тяжести кривой.

1.6 Нахождение статического момента и центра тяжести плоской фигуры.

1.7 Механическая работа.

2. Двойной интеграл.

2.1 Вычисление площади в случае прямоугольной области.

2.2 Вычисление площади в случае криволинейной области.

2.3 Вычисление объёма цилиндрического бруса.

2.4 Механические приложения.

3. Криволинейный интеграл.

3.1 Выражение площади с помощью криволинейных интегралов.

3.2 Приложения к физическим задачам.

4. Поверхностный интеграл.

4.1 Площадь поверхности, заданной явным уравнением.

4.2 Площадь поверхности в общем случае.

5.Тройной интеграл.

5.1 Масса тела. Объём.

5.2 Замена переменной в тройном интеграле.

Заключение.

 

 

Вступление

 

Известно, какие замечательные и разнообразные приложения имеет математический анализ как в самой математике, так и в смежных областях знания. Поэтому сама мысль о связи математического анализа с другими математическими дисциплинами и с потребностями практики должна быть усвоена учащимися при изучении основ анализа уже в школе. Изложенный в данной работе материал лишь немногим связан со школьным курсом. В школе в 10-11 классах изучаются неопределённые и определённые интегралы, практикуется вычисление простейших интегралов и нахождение площади криволинейной трапеции, что составляет лишь малую часть всего интегрального исчисления.

интеграл площадь объем статический момент

Определённый интеграл

Площадь криволинейной трапеции

 

Вычислим площадь плоских фигур при помощи интегралов.

На первом месте рассмотрим в строгом изложении задачу об определении площади криволинейной трапеции  (чертёж 1). Эта фигура ограничена сверху кривой , имеющей уравнение , где - положительная и непрерывная в промежутке  функция; снизу она ограничена отрезком  оси , а с боков – двумя ординатами  и (каждая из которых может свестись к точке).

 

Чертёж 1.

 

Так как площадь P рассматриваемой фигуры ABCD существует, то будем вести речь лишь об её вычислении. С этой целью разобьём промежуток  на части, вставив между a и b ряд точек . Обозначив через  и , соответственно, наибольшее и наименьшее значения функции  в i -м промежутке(i=0,1,…,n-1), составим суммы (Дарбу)

 

, .

Они, очевидно, представляют собой площади ступенчатых фигур, составленных, соответственно, из входящих и выходящих прямоугольников(см. чертёж). Поэтому . Но при стремлении к нулю наибольшей из разностей  обе суммы имеют своим пределом интеграл , следовательно, ему и равна искомая площадь P= . (1)

Если криволинейная трапеция CDFE ограничена и снизу и сверху кривыми (чертёж 2), уравнения которых  и , то, рассматривая её как разность двух фигур и , получим площадь названной трапеции в виде P= . (2)

Пусть теперь дан сектор AOB (чертёж 3), ограниченной кривой AB и двумя радиусами-векторами AO и OB (каждый из которых может свестись к точке). При этом кривая AB задаётся полярным уравнением , где  - положительная непрерывная в промежутке  функция.

 

 

Чертёж 2.                                                 Чертёж 3.

 

Вставив между  и  (см. чертёж) значения , проведём соответствующие этим углам радиус-векторы. Если ввести и здесь наименьшее и наибольшее значение функции  в  и , то круговые секторы, описанные этими радиусами, будут, соответственно, входящими и выходящими для фигуры(P). Составим отдельно из выходящих секторов две фигуры, площади которых будут  и .

 

 

В этих суммах  и  легко узнать суммы Дарбу для интеграла ; при стремлении к нулю наибольшей из разностей  обе они имеют пределом этот интеграл. Тогда фигура (P) квадрируема и P= . (3)

Примеры:

1). Определить площадь фигуры, заключённой между двумя конгруэнтными параболами  и  (чертёж 4).

Очевидно, нужно воспользоваться формулой (2), полагая там , . чертёж 4.

Для установления промежутка интегрирования решим совместно данные уравнения и найдём абсциссу точки M пересечения обеих парабол, отличной от начала; она равна 2 p. Имеем

 

.

 

2). Формула (1) может быть использована и в том случае, если кривая, ограничивающая криволинейную трапецию, задана параметрически или уравнениями , . . Произведя замену в интеграле (1), получим (в предположении, что  при  и  при ): . (4)

Если, например, при вычислении площади эллипса исходить из его параметрического представления ,  и учесть, что  возрастает от до , когда  убывает от  до нуля, то найдём . Мы вычислили площадь верхней половины эллипса и удвоили её.

 

 

 

Чертёж 5.

 

 

3). Найти площадь одного витка архимедовой спирали (чертёж 6).

Имеем по формуле (3) , в то время как площадь круга радиуса  будет . Площадь витка спирали равна трети площади круга (этот результат был известен ещё Архимеду). чертёж 6.

4). Аналогично вычисляется площадь фигуры, ограниченной циклоидой

 

,  (чертёж 5). Имеем по формуле (4)

.

 

Таким образом, искомая площадь оказалась равна утроенной площади круга радиуса a.

 

Объём тела

 

Начнём с почти очевидного замечания: прямой цилиндр высоты H, основанием которого служит квадрируемая плоская фигура (P), имеет объём, равный произведению площади основания на высоту: .

Возьмём многоугольники  и , соответственно содержащиеся в (P), так, чтобы их площади  и  стремились к P. Если на этих многоугольниках построить прямые призмы  и  высоты H, то их объёмы  и  будут стремиться к общему пределу , который и будет объёмом нашего цилиндра

 

 

 

Рассмотрим теперь некоторое тело (V), содержащееся между плоскостями  и , и станем рассекать его плоскостями, перпендикулярными к оси x (чертёж 7). Допустим, что (чертёж 7) все эти сечения квадрируемы, и пусть площадь сечения, отвечающего абсциссе x, - обозначим её через P(x) – будет непрерывной функцией от x (для ).

Если спроектировать без искажения два подобных сечения на какую-либо плоскость, перпендикулярную к оси x, то они могут либо содержаться одно в другом (чертёж 8а), либо частично одно на другое налегать, (чертёж 8) или лежать одно вне другого (чертёж 8б и 8в). Мы остановимся на том случае, когда два различных сечения, будучи спроектированы на плоскость, перпендикулярную к оси x, оказываются всегда содержащимися одно в другом.

В этом предположении можно утверждать, что тело имеет объём, который выражается формулой . (5)

Для доказательства разобьём отрезок  на оси x точками  на части и разложим плоскостями , проведёнными через точки деления, всё тело на слои. Рассмотрим i -й слой, содержащийся между плоскостями  и (i= 0,1,…, n -1). В промежутке  функция P (x) имеет наибольшее значение  и . Если сечения, отвечающие различным значениям x в этом промежутке, поместить на одну плоскость, скажем, , то все они при сделанном предположении будут содержаться в наибольшем, имеющем площадь , и содержать в себе наименьшее, с площадью . Если на этих, наибольшем и наименьшем, сечениях построить прямые цилиндры высоты , то больший из них будет содержать в себе рассматриваемый слой нашего тела, а меньший сам будет содержаться в этом слое. На основании сделанного вначале замечания объёмы этих цилиндров будут, соответственно,  и .

Из входящих цилиндров составится тело (T), а из выходящих – тело (U). Их объёмы равны, соответственно,  и  и, когда стремится к нулю , имеют общий предел (5). Значит таков же будет и объём тела(V).

 

 

Важный частный случай, когда заведомо выполняется указанное выше предположение о взаимном расположении сечений, представляют тела вращения. Вообразим на плоскости xy кривую, заданную уравнением , где  непрерывна и неотрицательна. Станем вращать ограниченную её криволинейную трапецию вокруг оси x (чертёж 9а и 9б). Полученное тело (V), очевидно, подходит под рассматриваемый случай, ибо сечения его проектируются на перпендикулярную к оси x плоскость в виде концентрических кругов. Здесь , так что

 

.

 

Если криволинейная трапеция ограничена (чертёж 9)

и сверху и снизу кривыми  и , то очевидно,

 

, (7)

 

Хотя предположение о сечениях здесь может и не выполняться. Вообще доказанный результат легко распространяется на все такие тела, которые получаются путём сложения или вычитания из тел, удовлетворяющих упомянутому предположению.

В общем случае можно утверждать лишь следующее: если тело (V) имеет объём, то он выражается формулой (6).

Примеры: 1). Пусть эллипс  вращается вокруг оси x. Так как , то для объёма эллипсоида вращения найдём

 

.

 

Аналогично для объёма тела, полученного от вращения вокруг оси y, найдём выражение  . Предполагая же в этих формулах , мы получим для объёма щара радиуса r известное значение .

2). То же – для ветви циклоиды , (). Параметрическое уравнение кривой облегчают выполнение подстановки ,  в формуле . Именно:

 

.

 

 

3). Найти объём трёхосного эллипсоида, заданного каноническим уравнением  (чертёж 10).

Плоскость, перпендикулярная к оси x и проходящая через точку M(x) на этой оси, пересечёт эллипсоид по эллипсу. Уравнение проекции его (без искажения) на плоскость yz будет таково: (чертёж 10).

 

, (x =const).

 

Отсюда ясно, что полуоси его будут, соответственно,

 

 и ,

 

а площадь выразится так: .

Таким образом, по формуле (5) искомый объём .

 

Длина дуги

 

Для начала введём понятия о спрямляемой дуге и её длины.

Рассмотрим на плоскости кривую AB, заданную параметрическими уравнениями , , (), (8)

 

 

где функци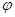и  и 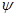 предполагаются непрерывными. Будем считать, что точка A отвечает значению , а точка B значению . При этом пусть кратных точек на кривой нет, так что различным значениям параметра  отвечают и различные точки кривой.

Если считать точки кривой (чертёж 11) расположенными в порядке возрастания параметра  (т.е. из двух точек ту принимать за следующую, которая отвечает большему значению параметра), то этим на кривой создаётся определённое направление (чертёж 11). Возьмём теперь на кривой AB ряд точек , идущих одна за другой в указанном направлении. Им отвечает ряд возрастающих значений параметра . Впишем в кривую AB ломаную  и обозначим через p её периметр. Конечный предел s для периметра p, при стремлении к нулю наибольшей из сторон  ломаной (p), называется длиной дуги: . Если такой предел существует, то сама кривая называется спрямляемой.

Перейдём непосредственно к выражению длины дуги интегралом.

Предположим дополнительно, что функци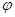и  и , фигурирующие в уравнениях (8) незамкнутой кривой, имеют непрерывные производные  и .

При этих условиях, как мы докажем, кривая спрямляема и длина дуги выражается формулой . (9)

Будем исходить из разбиения промежутка  точками  на части длины . Этим значениям t отвечают вершины ломаной , вписанной в дугу , и длину её можно определить как предел периметра P ломаной при стремлении  к нулю. Положим ,  и , .

Длина i -ого звена  вписанной ломаной выразится так: .

Применив к приращениям  и  функции порознь формулу конечных приращений, получим:

, , причём о значениях  и  мы ничего не знаем, кроме того, что оба они содержатся между  и . Имеем теперь , так что для периметра всей ломаной получается следующее выражение:

 

.

 

Если заменить во втором слагаемом под знаком корня везде  на , то преобразованное выражение , очевидно, представит собой интегральную сумму как раз для интеграла (9). При стремлении  к нулю эта сумма и будет своим пределом упомянутый интеграл. Для того, чтобы показать, что к тому же пределу стремится и периметр P ломаной, достаточно обнаружить, что разность  стремится к нулю.

С этой целью произведём оценку этой разности . Элементарное неравенство , если применить его к каждому слагаемому написанной выше суммы в отдельности, даст нам . Ввиду непрерывности функции , по любому заданному  найдётся такое ,  лишь только . Если взять все , так что  и . Это и доказывает наше утверждение.

Если кривая задана явным уравнением в прямоугольных координатах , то, принимая x за параметр, из формулы (9), как её частный случай, получим . (9а)

Наконец, и случай полярного задания кривой  также приводится к параметрическому с помощью обычных формул перехода , ; роль параметра здесь играет . Для этого случая , , так что  и . (9б)

Примеры:

1). Парабола: . Приняв за начало отсчёта дуг вершину O(x=0), для произвольной точки M c абсциссой x имеем:

 

 

2). Эллипс: . Удобнее взять уравнение эллипса в параметрической форме: , . Очевидно,

, где  есть численный эксцентриситет эллипса. Вычисляя длину дуги эллипса от верхнего конца малой оси до любой его точки в первом квадранте, .

Таким образом, длина дуги эллипса выражается эллиптическим интегралом второго рода; как указывалось, этот факт послужил поводом для названия «эллиптический».

В частности, длина четверти обвода эллипса выражается через полный эллиптический интеграл . Длина же всего обвода будет .